引言

上一节介绍了深度信念网络的模型表示，本节将介绍深度信念网络的模型构建思想——受限玻尔兹曼机叠加结构的基本逻辑。

回顾：深度信念网络的结构表示

深度信念网络是一个基于有向图、无向图的混合模型。它的概率图结构表示如下：

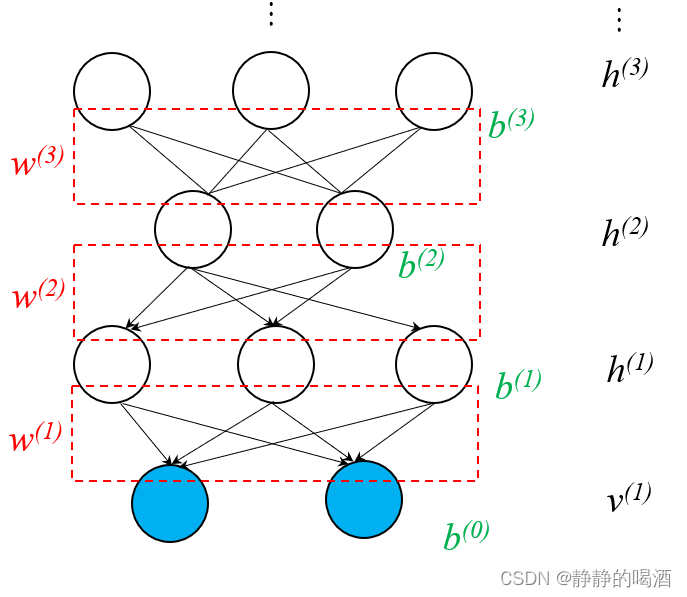
通过概率图结构的描述，可以发现：

• 观测变量层$v^{(1)}$，隐变量层$h^{(1)},h^{(2)}$三层的随机变量构成的概率图结构是Sigmoid信念网络；而隐变量层$h^{(2)},h^{(3)}$构成的概率图结构是受限玻尔兹曼机。
• 通过对受限玻尔兹曼机的堆叠(Stacking)实现对深度信念网络向更深层次进行延伸。
  这里使用省略号替代了后续的堆叠部分。

如果将随机变量层$v^{(1)},h^{(1)},h^{(2)},h^{(3)},\cdots$看作是关于对应层所有随机变量的集合，那么联合概率分布则表示为：
这里仍然以$v^{(1)},h^{(1)},h^{(2)},h^{(3)}$这四层结构进行示例。
$$\mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})$$
实际上，非相邻层之间存在条件独立性。

• 例如：$v^{(1)}$层与$h^{(2)}$层。这明显是有向图结构中的顺序结构。在$h^{(1)}$层可观测的条件下，$h^{(2)}$层中的任意结点与$v^{(1)}$层之间条件独立：
  $$h^{(2)}\perp v^{(1)}\mid h^{(1)}$$
• 上述只是有向图结构。如果是混合结构呢？例如：$h^{(1)}$层与$h^{(3)}$层。虽然既包含有向图结构，也包含无向图结构，但它们依然满足条件独立性：
  $$h^{(1)}\perp h^{(3)}\mid h^{(2)}$$
  以$h^{(1)},h^{(2)},h^{(3)}$层中的某一组结构为例，具体概率图结构表示如下(红色路径)：
  
  从有向图的角度观察，可以将红色部分表示为如下形式。如果在隐变量$h_j^{(2)}$给定的条件下，隐变量$h_k^{(3)},h_i^{(1)}$之间要么是顺序结构关系，要么是同父结构关系，依然改变不了条件独立的本质。
  

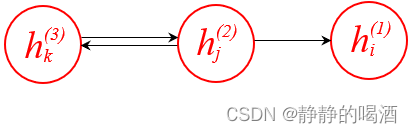
至此，联合概率分布$\mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})$可表示为：
$$\begin{array}{rl}\mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})& =\mathcal{P}(v^{(1)}\mid h^{(1)},h^{(2)},h^{(3)})\cdot \mathcal{P}(h^{(1)},h^{(2)},h^{(3)})\\ & =\mathcal{P}(v^{(1)}\mid h^{(1)})\cdot \mathcal{P}(h^{(1)}\mid h^{(2)},h^{(3)})\cdot \mathcal{P}(h^{(2)},h^{(3)})\\ & =\mathcal{P}(v^{(1)}\mid h^{(1)})\cdot \mathcal{P}(h^{(1)}\mid h^{(2)})\cdot \mathcal{P}(h^{(2)},h^{(3)})\end{array}$$
根据Sigmoid信念网络与受限玻尔兹曼机的定义，展开结果表示如下：
$$\begin{array}{rl}& \mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})=\prod _{i=1}^{\mathcal{D}}\mathcal{P}(v_i^{(1)}\mid h^{(1)})\cdot \prod _{j=1}^{{\mathcal{P}}^{(1)}}\mathcal{P}(h_j^{(1)}\mid h^{(2)})\cdot \mathcal{P}(h^{(2)},h^{(3)})\\ & \{\begin{array}{l}\mathcal{P}(v_i^{(1)}\mid h^{(1)})=\text{Sigmoid}\left\{{\left[{\mathcal{W}}_{h^{(1)}\to v_i^{(1)}}\right]}^T{h}^{(1)}+b_i^{(0)}\right\}{\left[{\mathcal{W}}_{h^{(1)}\to v_i^{(1)}}\right]}_{{\mathcal{P}}^{(1)}\times 1}\in {\mathcal{W}}^{(1)}\\ \mathcal{P}(h_j^{(1)}\mid h^{(2)})=\text{Sigmoid}\left\{{\left[{\mathcal{W}}_{h^{(2)}\to h_j^{(1)}}\right]}^T{h}^{(2)}+b_j^{(1)}\right\}{\left[{\mathcal{W}}_{h^{(2)}\to h_j^{(1)}}\right]}_{{\mathcal{P}}^{(2)}\times 1}\in {\mathcal{W}}^{(2)}\\ \mathcal{P}(h^{(2)},h^{(3)})=\frac{1}{\mathcal{Z}}\exp \left\{{\left[h^{(3)}\right]}^T{\mathcal{W}}^{(3)}\cdot h^{(2)}+{\left[h^{(2)}\right]}^T\cdot b^{(2)}+{\left[h^{(3)}\right]}^T{b}^{(3)}\right\}\end{array}\end{array}$$

解析RBM隐变量的先验概率

深度信念网络被设计成$\text{Sigmoid}$信念网络与若干受限玻尔兹曼机的叠加结构，它的设计思路具体是什么？
回顾受限玻尔兹曼机。其概率图结构表示如下：

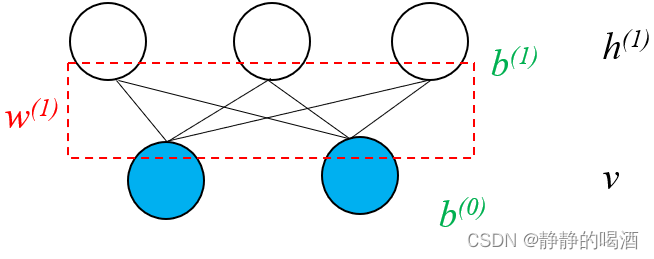
其中${\mathcal{W}}^{(1)}$表示隐变量、观测变量之间关联关系的权重信息；$b^{(0)},b^{(1)}$分别表示观测变量、隐变量的偏置信息。在受限玻尔兹曼机——对数似然梯度求解中，介绍了关于 模型参数$\theta$ 的求解过程：

• 根据已知样本 V = { v ( i ) } i = 1 N \mathcal V = \{v^{(i)}\}_{i=1}^N V={v(i)}i=1N​使用极大似然估计方法进行求解。其目标函数$\mathcal{L}(\theta )$表示为：
  $$\mathcal{L}(\theta )=\frac{1}{N}\sum _{v^{(i)}\in \mathcal{V}}\log \mathcal{P}(v^{(i)};\theta )$$
  对应模型参数的对数似然梯度可表示为：
  $${\nabla }_{\theta }\mathcal{L}(\theta )=\frac{1}{N}\sum _{v^{(i)}\in \mathcal{V}}{\nabla }_{\theta }\left[\log \mathcal{P}(v^{(i)};\theta )\right]$$
• 根据能量模型的对数似然梯度，将${\nabla }_{\theta }\left[\log \mathcal{P}(v^{(i)};\theta )\right]$表示为如下形式：
  $${\nabla }_{\theta }\left[\log \mathcal{P}(v^{(i)};\theta )\right]=\mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}-\sum _{v^{(i)}}\mathcal{P}(v^{(i)})\cdot \mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}\theta ={\mathcal{W}}_{h_k^{(i)}\iff v_j^{(i)}}$$
  关于第一项：可以通过$\text{Sigmoid}$函数直接求解后验概率$\mathcal{P}(h_k^{(i)}=1\mid v^{(i)})$；
  关于第二项：它是关于$N$项的连加，其计算量极高。因而通过使用对比散度的方式对第二项进行近似：
  这里的$t$表示吉布斯采样的迭代步骤。
  $$\sum _{v^{(i)}}\mathcal{P}(v^{(i)})\cdot \mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}={\mathbb{E}}_{v^{(k)}\sim \mathcal{P}({\mathcal{V}}^{t=k})}\left[\mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}\right]$$
• 关于参数${\mathcal{W}}_{h_k^{(i)}\iff v_j^{(i)}}$的梯度求解完成后，使用梯度上升法近似求解${\mathcal{W}}_{h_k^{(i)}\iff v_j^{(i)}}$。其余参数同理：
  $${\theta }^{(t+1)}\Leftarrow {\theta }^{(t)}+\eta {\nabla }_{\theta }\left[\log \mathcal{P}(v^{(i)};\theta )\right]\theta ={\mathcal{W}}_{h_k^{(i)}\iff v_j^{(i)}}$$

观察，上述关于模型参数的学习过程是复杂的，并且包含两次近似(对比散度、梯度上升)，其核心原因在于：受限玻尔兹曼机是一个无向图模型，随机变量结点之间没有明确的因果关系。
能否通过一些改进，让参数学习过程的效果更好？
以上述受限玻尔兹曼机概率图结构示例，再次将关注点转向$\mathcal{P}(v)$：
这里的上标就变成了网络层的编号，而不是样本编号。
$$\begin{array}{rl}\mathcal{P}(v)& =\sum _{h^{(1)}}\mathcal{P}(h^{(1)},v)\\ & =\sum _{h^{(1)}}\mathcal{P}(h^{(1)})\cdot \mathcal{P}(v\mid h^{(1)})\end{array}$$

• 其中$h^{(1)}$可看成$\text{RBM}$中所有隐变量的随机变量集合，$v$则是所有观测变量的随机变量集合，而$h^{(1)}$中的随机变量不是真实的，而是基于模型假定的。因此，称$\mathcal{P}(h^{(1)})$为 先验概率；
• 而$\mathcal{P}(v\mid h^{(1)})$则是给定隐变量条件下，样本的 生成过程(Generative Process)。
  这些样本自然不是真实的，而是模型产生的‘幻想粒子’(Fantasy Particle).与幻想粒子相关的传送门

由于是无向图模型，因而同上，从有向图的角度观察，可以将图结构中的每一条边视作双向的。也就是相互关联：

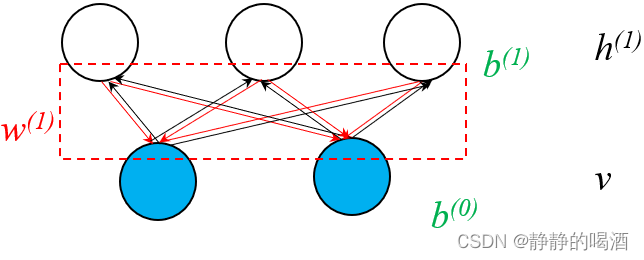
如果假设模型参数已经被学习完成，这意味着模型参数固定，$\mathcal{P}(v\mid h^{(1)})$也被固定住：
这里的$n$表示模型中观测变量的数量,$m$表示模型中隐变量的数量。相关推导过程见RBM推断任务——后验概率
$$\begin{array}{rl}\mathcal{P}(v\mid h^{(1)})& =\prod _{i=1}^n\mathcal{P}(v_i\mid h^{(1)})\\ \mathcal{P}(v_i\mid h)& =\{\begin{array}{l}\mathcal{P}(v_i=1\mid h)\Rightarrow \text{Sigmoid}\left({\sum }_{j=1}^m{w}_{ij}\cdot h_j+b_i\right)\\ \mathcal{P}(v_i=0\mid h)\Rightarrow 1-\text{Sigmoid}\left({\sum }_{j=1}^m{w}_{ij}\cdot h_j+b_i\right)\end{array}\end{array}$$
而$\mathcal{P}(v)$是真实样本关于随机变量的联合概率分布，自然是确定的：
相关推导过程详见RBM推断任务——边缘概率,这里的$b$表示各观测变量与自身的关联关系(常数，偏置)组成的向量。
$$\mathcal{P}(v)=\frac{1}{\mathcal{Z}}\exp \left\{b^{T}v+\sum _{j=1}^m\log \text{Softplus}({\mathcal{W}}_j^{T}v+c_j)\right\}$$
那么根据上式，先验概率$\mathcal{P}(h^{(1)})$自然也是确定的，它同样可以使用模型参数进行表示。

通过模型学习隐变量的先验概率

相比于使用模型参数表示先验概率$\mathcal{P}(h^{(1)})$，一个新的思路是：针对隐变量先验概率$\mathcal{P}(h^{(1)})$进行建模，通过模型将$\mathcal{P}(h^{(1)})$学习出来。也就是说，通过的受限玻尔兹曼机将隐变量的联合概率分布求解出来。

观察上图(黑色箭头)，利用真实样本使用醒眠算法的$\text{Weak Phase}$方法能够获得关于隐变量后验的样本，并基于这些样本，专门对隐变量进行训练：
也就是说，为了学习‘Sigmoid信念网络’中的隐变量，需要对隐变量进行建模，构建‘隐变量的隐变量’对其进行学习。

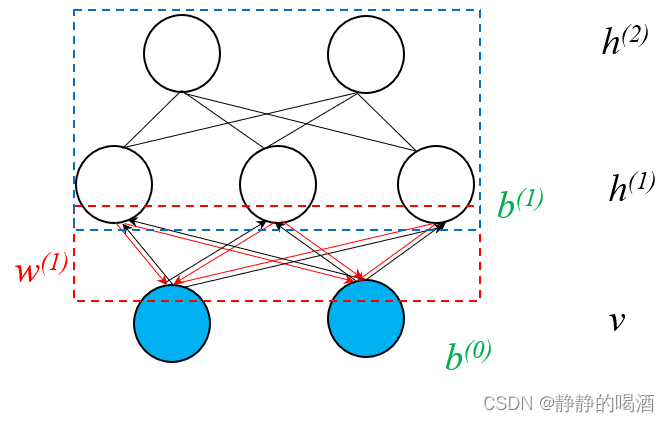
此时，关于$h^{(1)}$的边缘概率分布可表示为：
$$\sum _{h^{(2)}}\mathcal{P}(h^{(1)},h^{(2)})$$
很明显，$\mathcal{P}(h^{(1)},h^{(2)})$就是新构建受限玻尔兹曼机(蓝色框部分)的联合概率分布。此时将$h^{(1)}$在受限玻尔兹曼机中视作观测变量，基于$\mathcal{P}(h^{(1)}\mid v)$的后验样本，可以学习出该受限玻尔兹曼机的参数信息。通过这些参数信息产生的关于$h^{(1)}$的概率分布$\mathcal{P}(h^{(1)})$要优于原始模型参数学习的$\mathcal{P}(h^{(1)})$。

事实上，根据第一层受限玻尔兹曼机的逻辑，我们理论上可以将层数一直叠加上去，通过构建新的隐变量学习前一层隐变量的信息。
需要注意的是，这种堆叠式结构的求解方式是有约束条件的。那就是Weak Phase中关于隐变量$h^{(1)}$的后验概率分布$\mathcal{P}(h^{(1)}\mid v)$固定的条件下实现的。

• 如果不去固定$\mathcal{P}(h^{(1)}\mid v)$,在$h^{(2)}$学习$\mathcal{P}(h^{(1)})$过程中，由于$\mathcal{P}(h^{(1)}\mid v)$产生样本对应分布的细微变化(可能存在波动、噪声)，导致$h^{(1)},h^{(2)}$层之间的模型参数是无法被固定下来的。
• 相反，如果没有固定$\mathcal{P}(h^{(1)}\mid v)$,假设$h^{(1)},h^{(2)}$之间的模型参数被学习出来，学习得到的$\mathcal{P}(h^{(1)})$和$\mathcal{P}(h^{(1)}\mid v)$之间存在偏差，反而对$h^{(1)},v$层之间的权重信息产生影响。
当然，也可以从有向图的角度去理解该问题。如果出现了如下结构：
  
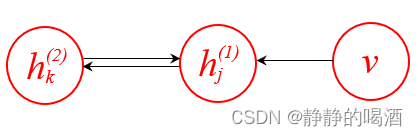
  这种结构保留了$v\Rightarrow h^{(1)}$之间的关联关系，我们会发现，$v,h^{(2)}$之间不是完全的‘无关联’关系。因为内部包含一个$\mathcal{V}$型结构。一旦经过$\text{Weak Phase}$算法，得到了关于后验$\mathcal{P}(h^{(1)}\mid v)$的样本，此时结点$h^{(1)}$被观测，那么$h^{(2)},v$之间是必不独立的。

终上，为了保证学习$h^{(1)}$信息的受限玻尔兹曼机和$\text{Sigmoid}$信念网络之间相互不影响，将上图中 $v\Rightarrow h^{(1)}$ 部分去除：

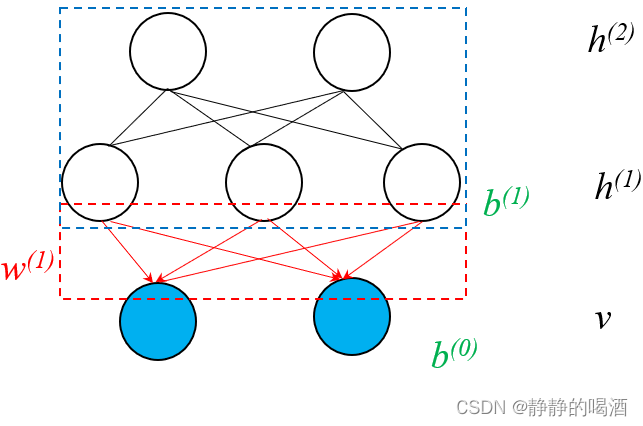
上面过程就是深度信念网络模型的构建思想。
这里只是提到了使用受限玻尔兹曼机对隐变量的学习效果优于模型参数对隐变量的表示效果。下一节将解释为什么对隐变量建模的效果更优。

相关参考：
(系列二十七)深度信念网络2——叠加RBM的动机