论文：《 Subpixel edge detection based on edge gradient directional interpolation and Zernike moment》
地址： http://www.dpi-proceedings.com/index.php/dtcse/article/view/24488

摘要

在本文中，我们提出了一种基于边缘梯度方向插值和 Zernike 正交矩的新型亚像素边缘检测方法。由于对边缘邻域进行插值，所提出的方法能够丰富边缘信息，并确保矩模板内只有一个边缘。边缘信息的丰富不仅增加了基于矩的方法的检测精度，还增加了检测到的亚像素边缘点的数量。实验结果表明，该方法可以极大地提高边缘检测的准确性，并且在图像中存在复杂边缘时能够避免边缘干扰的问题。

一、引言

边缘检测是图像处理中的基本任务。传统基于梯度的边缘检测方法只能定位到像素级别的边缘。一般来说，通过增加采样频率可以提高边缘检测的准确性。然而，最大采样率受到物理设备条件的限制，无法无限增加。此外，在实际的工业应用中，成本也是一个重要的不可避免的考虑因素。这一问题导致了亚像素边缘检测算法的诞生。亚像素边缘检测可以理解为一种通过图像处理算法，在不改变摄像机系统硬件条件的情况下使边缘精度小于一个像素的方法。
早期的边缘检测算法是基于梯度的，通过计算局部梯度或导数的最大值来定位边缘点。其中最典型的算子包括 Sobel、Prewitt 和 Robert 算子。后来，Canny 综合了以前的工作，提出了一种基于非极大值抑制和形态连通操作的方法来寻找最优边缘。这种方法取得了良好的结果，并且在今天被广泛使用。其他的边缘检测算法包括 Malik 的边缘检测方法，这种方法很出色，但也比较复杂。其他像素级边缘检测算法可以在文献[6-8]中找到。对于亚像素边缘检测，目前流行的方法包括基于拟合的方法、基于矩的方法和基于插值的方法。拟合方法是通过拟合假设边缘模型的灰度值来解决亚像素边缘位置的方法，通常是基于高斯函数的边缘模型。插值方法的核心思想是通过插值像素的灰度值或灰度值的导数来增加边缘信息。二次插值算法简单且易于实现。特别是当光学系统的扩散函数是对称的时，插值边缘的检测精度很高。然而，其缺点是容易受到噪声的干扰。基于矩的方法的核心思想是利用图像的矩信息来解决边缘参数。矩有很多种，例如空间矩、Zernike 矩等。Ghosal 首先使用的 Zernike 矩方法只需要计算3个模板。计算量比空间矩小，精度也高。后来，Qu 提出了一个改进算法，通过增加 Zernike 矩的阶数或增加模板的大小来提高亚像素定位的准确性。
目前，通过矩方法检测亚像素已被证明是一种简单而准确的方法。即便如此，在实际应用中，并没有一种普遍适用的方法，精度仍有很大提升空间。基于矩的建模是基于图像边缘是理想的阶跃边缘的假设。为了提高检测精度，一个有效且简单的方法是增加矩的模板大小。然而，当模板内部存在复杂的边缘时，这些边缘可能会相互干扰，导致边缘定位错误。由于很难确保模板内只有一个边缘，如果模板内存在多个边缘，那么就需要重新对边缘进行建模。然而，经过分析，普遍重新对边缘进行建模不仅困难，而且很难获得准确的分析解决方案。通过严格的边缘参数重新建模图像边缘也很难找到尽可能多的亚像素边缘点。此外，基于严格的边缘参数重新建模后的阈值进行后续边缘过滤也非常复杂。随着硬件计算的快速加速，更精确的方法也随之而来。
通过总结亚像素边缘检测算法的优缺点，本文提出了一种改进方法。首先，基于像素级别获得边缘的粗略位置，并追踪边缘点的邻域。为了提高边缘的准确性，同时避免上述问题，本文提出通过在边缘邻域进行梯度方向的插值来丰富边缘信息。由于对边缘邻域进行了插值，扩大了矩模板进行卷积的区域。因此，能够确保模板内只有一个边缘，从而有效地避免了边缘之间的干扰。同时，丰富的边缘信息不仅增加了基于矩方法的检测准确性，还增加了检测到的亚像素边缘点的数量。此外，如果在插值后对邻域进行Canny像素级边缘定位操作，则可以检测到双边缘，这意味着可以获得具有厚度特性的亚像素边缘。最后，采用大规模掩模Zernike矩方法来检测邻域边缘并推导出亚像素级别的边缘参数。
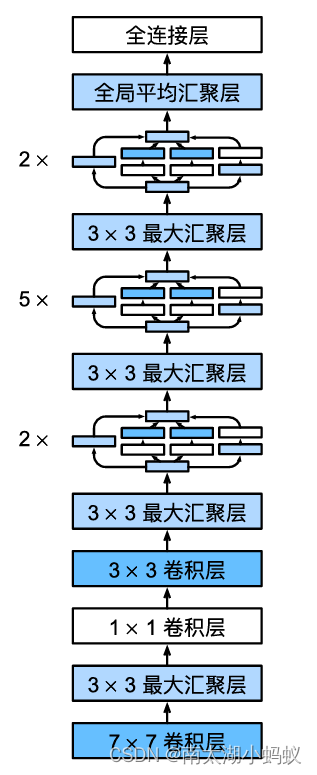
本文的结构如下所述。第3节简要介绍了Zernike矩的原理。在第4节中，讨论了基于7*7掩模的Zernike矩的亚像素边缘检测，并给出了理论推导。第5节讨论了在边缘点邻域内的梯度插值方法。在第6节中，设计了两个实验来验证边缘亚像素定位的准确性以及复杂边缘定位的能力。最后，在第7节中给出了一些结论。

二、Zernike图像矩

在连续域中，可以证明一个函数可以用单位圆内的多项式的组合来描述，即$x^2+y^2\le 1$。Zernike 多项式是一种正交完备的多项式，因此函数可以无冗余地描述。对于一幅图像$f(x,y)$ 的阶数为 $n$ 且重复次数为$m$的 Zernike 矩被定义为 [17]：
$$Z_{nm}=\frac{n+1}{\pi }{\iint }_{x^2+y^2\le 1}f(x,y)V_{nm}^{\ast }(\rho ,\theta )dxdy(1)$$
在离散图像中，当$x^2+y^2\le 1$ 时，$Z_{(}nm)$可以如下表示，其中 $n$ 和$m$ 是非负整数。
$$Z_{nm}={\Sigma }_x{\Sigma }_{y}f(x,y),V_{nm}^{\ast }(\rho ,\theta )(2)$$
Zernike多项式$V_{nm}$可以表示为：
$$V_{nm}=R_{nm}(\rho )e^{im\theta },|\rho |\le 1(3)$$

其中$R_{nm}(\rho )$是径向函数，当$n-m$是奇数时，$R_{nm}(\rho )=0$。当$n-m$是偶数时，$R_{nm}(\rho )$可以表示为:
$$R_{nm}(\rho )={\Sigma }_{k=0}^{(n-|\mathbf{m}|)/2}\frac{(-1{)}^k(n-k)!}{k!(\frac{n+|\mathbf{m}|}{2}-k)!(\frac{n-|\mathbf{m}|}{2}-k)!}{\rho }^{n-2k}(4)$$

结合方程 (2) 和 (3) 计算 Zernike 多项式。因此，我们可以通过查表来找到 Zernike 多项式 $V_{nm}$。根据方程 (2)，我们可以轻松地计算图像$f(x,y)$的 Zernike 矩。此外，Zernike 矩具有一个重要的特性，即旋转不变性，即:

$$Z_{nm}^{\prime }=Z_{nme}^{}-im\varphi (5)$$

其中 $Z_{nm}^{\prime }$ 是旋转后图像的 Zernike 矩，$Z_{nm}$是原始图像的 Zernike 矩。方程 (5) 显示了图像旋转后 Zernike 矩的变化，即旋转后图像的 Zernike 矩的大小，而原始图像的 Zernike 矩不会改变。

基于Zernike Moment的边缘检测

为了定位亚像素边缘位置，建立一个2-D单位圆模型，其中有一个理想的阶跃边缘。正如图1所示，$k$是阶跃的高度，$h$是背景的高度，$l$是边缘与单位圆中心之间的距离。当理想的边缘线旋转时，它将垂直于$x$轴。接下来，我们将使用Zernike矩来计算这组边缘位置参数，即$h、k、l$。

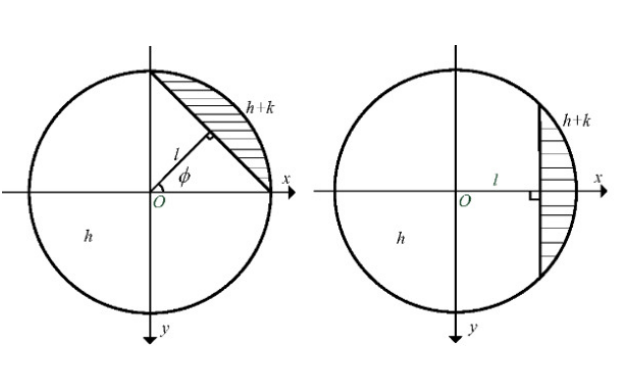
图1. 亚像素边缘检测的理想模型。

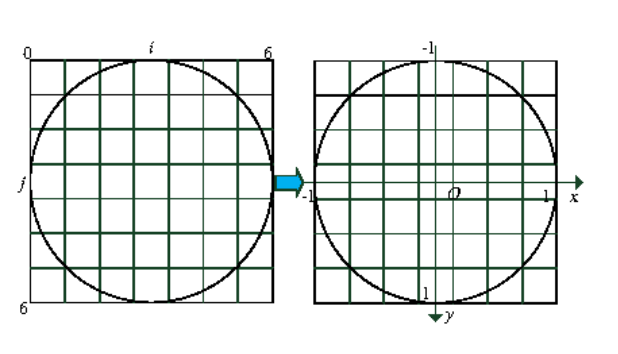
图2. Zernike 7*7掩码模型。

现在假设这个模型是$f(x,y)$，根据方程（2）和方程（5）计算其旋转的 Zernike 矩 7。解方程得到$ ℎ,k,l$ 的值
$$k=\frac{3Z^{\prime }}{2(1-l_2^2{)}^{3/2}}(6)$$
$$h=\frac{1}{\pi }[Z_{00}-\frac{k\pi }{2}+karcsin(l_2)+k{l}_2\sqrt{1-l_2^2}](7)$$
$$l=\frac{l_1+l_2}{2}=\frac{1}{2}[\sqrt{\frac{5Z_{40}^{\prime }+3Z_{20}^{\prime }}{8Z_{20}^{\prime }}}+\sqrt{\frac{5Z_{11}^{\prime }+Z_{11}^{\prime }}{6Z_{11}^{\prime }}}](8)$$
$$\varphi =\arctan \left[\frac{Im[Z_{n1}]}{Re[Z_{n1}]}\right](9)$$

如上所述，我们推导出边缘参数 $h,k,l$和$\varphi$。因此，边缘在单位圆内的亚像素位置可以标记为
$$\left[\begin{array}{c}{x}_s\\ y_s\end{array}\right]=\left[\begin{array}{c}x+l\cos (\varphi )\\ y+l\sin (\varphi )\end{array}\right](10)$$

然而，$(x,y)$在实际的离散图像中，我们使用$N\ast N$像素范围来近似单位圆，如图2所示。单位圆被划分为$7\ast 7$个区域。上述计算结果基于单位圆内的$7\ast 7$区域。我们将实际图像上每个点的像素值放入单位圆的$7\ast 7$区域中，以计算亚像素边缘参数。但实际上，将一个像素划分为$7\ast 7$个邻域是不可能的。因此，从单位圆导出的边缘位置参数$l$最终要乘以缩放因子$N/2$。只有这样，才能检测到图像边缘的亚像素位置。
$$Subpixel=\left[{}_{y_s}^{X_s}\right]==\left[\begin{array}{l}x+\frac{lN}{2}\cos (\varphi )\\ y+\frac{lN}{2}\sin (\varphi )\end{array}\right](11)$$

从以上讨论可以得知，通过推导图像的$M_{n1}$阶矩，可以使用方程（9）计算；然后，我们推导出图像的其他Zernike矩，并得到旋转后的图像Zernike矩。最后，我们通过方程（7）、（6）、（8）获得边缘参数 $h,k,l$。因此，在图像的$N\ast N$区域内计算Zernike矩非常重要，这将决定整个检测的准确性。
为了近似图像的Zernike矩，我们构建了一系列的掩模，可以通过下面公式来导出：
$$M_{nm}(i,j)={\iint }_{{\Omega }_{i,j}=C\cap S_{i,j}}{V}_{nm}^{\ast }(\rho ,\theta )dxdy(12)$$

Zernike多项式是通过查找方程式（3）获得的，用于计算图像Zernike矩的掩模是通过Matlab计算获得的。将图像的每个点的N*N区域与这些掩模进行卷积，得到M
。
最后，通过将M
代入方程(6)(8)(7)(9)中，我们可以得到边缘的参数$h,k,l$的和。通过设置特征阈值$l_T,k_T$（如方程（13）（14）所示），我们可以过滤出特定的边缘位置或确保检测准确性。
$$l\le l_T(13)$$
$$k\ge k_T(14)$$

基于方向插值的亚像素边缘检测

与连续域中的讨论不同，由于图像的离散性，亚像素边缘的检测必然会存在误差。使用 Zernike 矩来定位边缘的亚像素，主要误差的原因是 $M_{nm}$mask 的大小。如果图像只有简单且稀疏的边缘，大尺寸的 mask 可以带来高精度。然而，正如在第1节中提到的，如果图像中存在彼此相邻的复杂边缘，边缘检测中将会出现误差。
$$Accuracy\propto N(15)$$
此外，当掩模覆盖区域内的边缘信息较少时，描绘细节的能力也较差。

为了克服这一限制，本文提出了一种改进的亚像素边缘检测算法。其原理是根据边缘的梯度方向进行插值，丰富其位置信息，使得大尺寸的 Zernike 矩掩模可以发挥其准确的边缘定位能力。

Canny 算法被应用于近似边缘点。边缘点的梯度 $f(x,y)$可以表示为:
$$gradf(x,y)=\nabla f(x,y)=\left\{\frac{\partial f(x,y)}{\partial x},\frac{\partial f(x,y)}{\partial y}\right\}(16)$$

边缘点场的梯度方向插值可以表示为
$$x_t=\lfloor C_t\frac{\partial f(x,y)}{\partial x}\rfloor ,y_t=\lfloor C_t\frac{\partial f(x,y)}{\partial y}\rfloor (17)$$

在公式17中，$x_t,y_t$表示边缘点在$N\ast N$域中在x方向和y方向上的扩展次数，$C_t$是一个常数，$\lfloor \rfloor$符号表示向上取整。
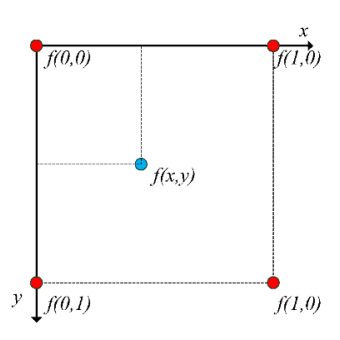
应用图3中显示的双线性插值方法对边缘点进行扩展。如图4所示，如果插值后的图像经过Canny检测，则可以获得双边缘信息。通过与原始边缘的映射信息，可以找到原始边缘的双边缘信息。这将进一步增加边缘亚像素的检测深度，并获得原始边缘更丰富的亚像素信息。
$$Subpixel=\left[\begin{array}{l}{x}_s\\ y_s\end{array}\right]=\left[\begin{array}{c}x/x_t+\frac{lN}{2x_t}\cos (\varphi )\\ y/y_t+\frac{lN}{2y_t}\sin (\varphi )\end{array}\right](18)$$
如图4所示，如果经过插值处理的图像经过Canny边缘检测，就可以获得双边缘信息。通过与原始边缘的映射信息，可以找到原始边缘的双边缘信息。这将进一步增加边缘亚像素的检测深度，并获得原始边缘更丰富的亚像素信息。