今日题目:
- 78. 子集
- 77. 组合
- 46. 全排列
- 90. 子集 II
- 47. 全排列 II
- 39. 组合总和
目录
- 1. 子集(元素无重不可复选) 【easy】
- 2. 组合(元素无重不可复选)
- 3. 排列(元素无重不可复选) 【classic】
- 4. 子集/组合(元素可重不可复选)【稍有难度】
- 5. 排列(元素可重不可复选)
- 6. 子集/组合(元素无重可复选)
无论是排列、组合还是子集问题,简单说无非就是让你从序列 nums 中以给定规则取若干元素。但无论形式怎么变化,其本质就是穷举所有解,而这些解呈现树形结构,所以合理使用回溯算法框架,稍改代码框架即可把这些问题一网打尽。
记住,在运用回溯算法来解决问题时,一定要用手画一下回溯树的构建思路,也就是说弄清楚在每一步如何做出选择以及递归结束的条件是什么。
1. 子集(元素无重不可复选) 【easy】
78. 子集
这个题目就很基本了,前面也做过,难度不大。
2. 组合(元素无重不可复选)
77. 组合
根据题目背景,确定好每次可以做的选择有哪些和递归结束的条件。难度也不大。
3. 排列(元素无重不可复选) 【classic】
46. 全排列
这个题目在 排列(元素无重不可复选)| labuladong 文章中借助于 used 巧妙地实现了标准全排列,值得参考学习。同时这篇文章提出的实现元素个数为 k 个的排列的方法也值得学习。
4. 子集/组合(元素可重不可复选)【稍有难度】
90. 子集 II
这个题目让返回 nums 的所有可能子集,且这些子集之间不能重复。注意 [1, 2, 2] 与 [2, 2, 1] 其实是同一个集合,是算作重复的,题目给的示例:

如果 nums 中没有重复元素的话,做这个题目的思路就是:在 backtrace 做选择时,每个元素有“选”和“不选”两种选择,从而得到所有的子集。
但如果 nums 中有重复元素的话,这个做法就有问题了,比如示例的 nums = [1, 2, 2],选第一个 2 不选第二个 2 是一种情况,不选第一个 2 选第二个 2 也是一种情况,但这两种情况得到的结果重复了,为了解决这个重复问题,我们就不让后者情况出现,也就是当第一个 2 选了之后,我们就绝对不再选第二个 2。具体代码实现就是,当检查到当前元素与前面重复且前面元素没有选的时候,当前元素就只有“不选”这一个选择了,如下所示:
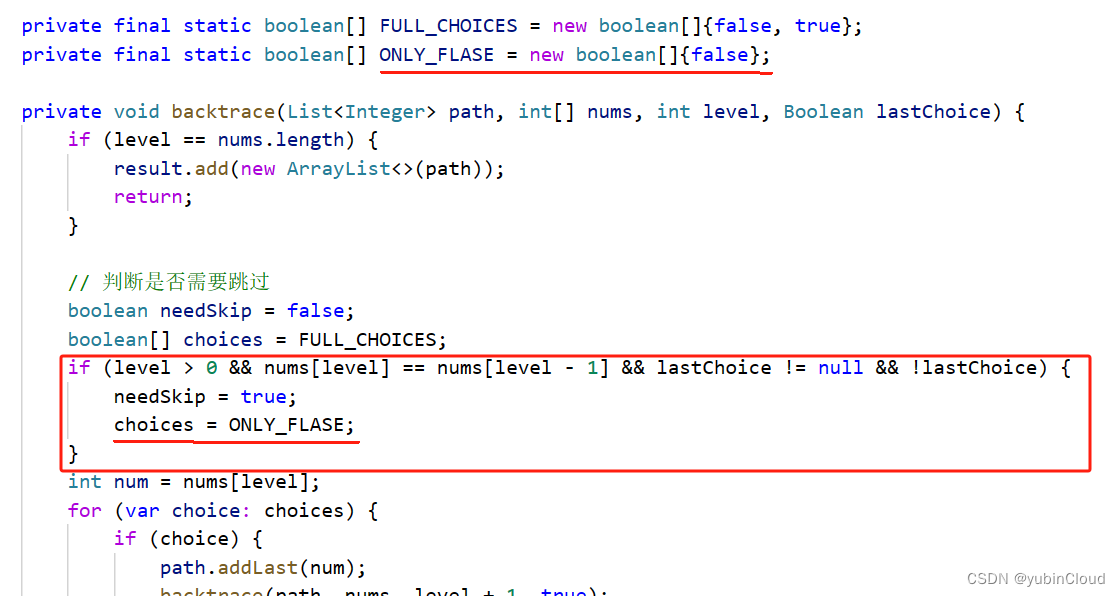
这里还有一个小坑,为了能够实现重复检测,我们这里需要事先对 nums 进行排序,从而让重复的元素能够聚在一块:

5. 排列(元素可重不可复选)
47. 全排列 II
也是 nums 中可能包含重复数字,且答案集合不允许重复。我这里投机取巧了,直接将 result 声明为 HashSet 从而实现过滤重复元素。
这里可以这样做的原因是,题目认为的答案重复的元素,HashSet 也会认为是重复从而过滤掉,但上个题目却不是,题目认为的答案重复的元素,HashSet 却不一定认为是重复,比如 [1, 2, 2] 和 [2, 2, 1]。这也是这个题可以投机取巧而上个题目不行的原因。
6. 子集/组合(元素无重可复选)
39. 组合总和
也是事先排序,这个题目的新颖点在于,每一次可以做的选择是不能事先确定的,而是动态计算出来的。理清好思路后难度也不大。