目录
4.1 序偶和笛卡尔积
4.1.1 有序组的定义
4.1.2 笛卡儿积
4.1.3 笛卡儿积的性质
4.1.4 推广
4.2 关系的定义
4.2.1 二元关系的定义
4.2.2 二元关系的数学符号
4.2.3 枚举二元关系
4.2.4 几种重要关系
4.2.5 定义域和值域
4.2.6 n元关系
4.3 关系的表示
4.3.1 关系的集合表示
4.3.2 关系的图形表示 (A≠B)
4.3.3 关系的图形表示 (A = B)
4.3.4 关系的矩阵表示
4.3.5 布尔矩阵的并和交运算
4.3.6 布尔矩阵的积运算
4.4 关系的运算
4.4.1 关系的并交差补运算
4.4.2 关系的复合运算
4.4.3 用三种关系表示法进行复合运算
4.4.4 关系的逆运算
4.4.5 用三种关系表示法求逆
4.5 关系的运算性质
4.5.1 结合律与同一律
4.5.2 分配律
4.5.3 逆运算
4.6 关系的幂运算
4.6.1 幂运算的定义
4.6.2 幂运算的收敛性
4.7 关系的性质 (一)
4.7.1 自反性与反自反性
4.7.2 对称性与反对称性
4.7.3 传递性
4.8 关系的性质 (二)
4.8.1 关系性质的判定定理
4.8.2 关系性质的保守性
4.9 关系的闭包
4.9.1 闭包定义
4.9.2 利用关系图求闭包
4.9.3 利用关系运算求闭包
4.1 序偶和笛卡尔积
4.1.1 有序组的定义
由两个元素按照一定的次序组成的二元组称为序偶,记作< x, y >,其中 x 是第一元素,y 是第二元素。
由定义可见,两个序偶< a, b >=< c, d >当且仅当a = c, b = d
4.1.2 笛卡儿积
设 A, B 是两个集合,称集合A×B= {< x, y > |(x ∈ A) ∧ (y ∈ B)} 为集合 A 与 B 的笛卡儿积
例如
集合 A = {1, 2}, B = {a, b, c} 的笛卡儿积
A × B = {< 1, a >, < 1, b >, < 1, c >, < 2, a >, < 2, b >, < 2, c >}
B × A = {< a, 1 >, < b, 1 >, < c, 1 >, < a, 2 >, < b, 2 >, < c, 2 >}
4.1.3 笛卡儿积的性质
- 设 A, B 是任意两个集合,则不一定有 A × B = B × A,即笛卡儿积不满足交换律
- A × B = ∅当且仅当 A = ∅或者 B = ∅
- 设 A,B, C 是任意三个集合,则不一定有 A × (B × C) = (A × B) × C,即笛卡儿积不满足结合律
- 当集合 A, B 都是有限集时,|A × B| = |B × A| = |A| × |B|。
- 笛卡儿积对并运算和交运算满足分配律
4.1.4 推广
由 n 个元素 a1, a2, · · · , an 按照一定次序组成的 n 元组称为n 重有序组,记作< a1, a2, · · · , an >. 其中 a1 是第一个元素,a2 是第二个元素,· · · ,an 是第 n 个元素。
设 A1, A2, · · · ,An 是 n 个集合,称集合A1 × A2 × · · · × An = {< a1, a2, …, an > |ai ∈ Ai, i = 1, 2, 3, · · · , n} 为集合 A1, A2, · · · ,An的笛卡儿积。当 A1 = A2 = · · · = An = A 时,可记 A1 × A2 × · · · × An = A^n。
两个 n 重有序组< a1, a2, · · · , an >=< b1, b2, b3, · · · , bn >当且仅当ai = bi,i = 1, 2, …, n
当集合 A1,A2, · · · , An 都是有限集时,|A1 × A2 × · · · × An| = |A1| × |A2| × · · · × |An|
4.2 关系的定义
4.2.1 二元关系的定义
设 A, B 为两个非空集合,称A × B 的任意子集 R 为从 A 到 B 的一个二元关系,简称关系 (relation)。其中,A 称为关系 R 的前域,B 称为关系 R 的后域。如果A = B,则称 R为A 上的一个二元关系。
4.2.2 二元关系的数学符号
若序偶 < x, y >∈ R,通常把这一事实记为 xRy,读作“x 对 y 有关系 R”
若序偶 < x, y >∉ R,通常把这一事实记为 x℞y,读作“x 对 y 没有关系 R”
4.2.3 枚举二元关系
假设 A = {a, b} B = {c, d},试写出从 A 到 B 的所有不同关系。
解 首先求两个集合的笛卡儿积:A × B = {< a, c >, < a, d >, < b, c >, < b, d >}。
再求 A × B 的所有不同子集:
0–元子集:∅;
1–元子集:{< a, c >}, {< a, d >}, {< b, c >}, {< b, d >};
2–元子集:{< a, c >, < a, d >},{< a, c >, < b, c >}, {< a, c >, < b, d >},{< a, d >, < b, d >},{< a, d >, < b, d >}, {< b, c >, < b, d >};
3–元子集:
{< a, c >, < a, d >, < b, c >},{< a, c >, < a, d >, < b, d >},{< a, c >, < b, c >, < b, d >},{< a, d >, < b, c >, < b, d >};
4–元子集:{< a, c >, < a, d >, < b, c >, < b, d >}。
所以,上面的 16 个不同子集就是从 A 到 B 的所有不同关系。
4.2.4 几种重要关系
- 当 R = ∅时,称 R 为从 A 到 B 的空关系(empty relation);
- 当 R = A × B 时,称 R 为从 A 到 B 的全关系(total relation);A 上的全关系通常记为 Eᴀ
- 当 R = Iᴀ = {< x, x > |x ∈ A} 时,称 R 为 A 上的恒等关系(identity relation)。
当集合 A, B 都是有限集时,A×B 共有 |A|×|B| 个不同的元素,这些元素将会产生 2^(|A|×|B|)个不同的子集。
即,从 A 到 B 的不同关系共有 2^(|A|×|B|) 个
4.2.5 定义域和值域
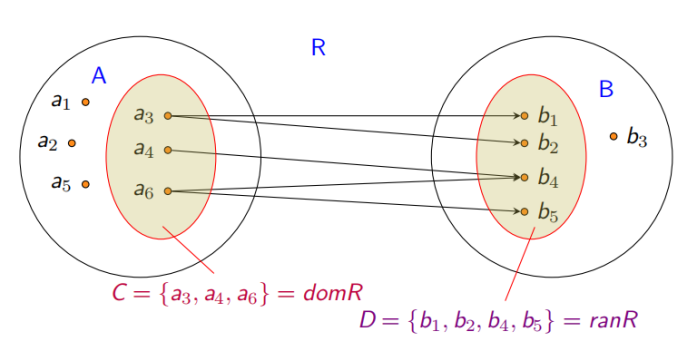
设 R 是从 A 到 B 的二元关系,则 A 为关系 R 的前域,B 为关系 R 的后域。令:C = {x|x ∈ A, ∃y ∈ B, < x, y >∈ R},D = {y|y ∈ B, ∃x ∈ A, < x, y >∈ R}。称 C 为 R的定义域(domain),记为 C = domR;D 为 R 的值域(range),记为 D = ranR;fldR = domR ∪ ranR 为 R 的域(field)
4.2.6 n元关系
设 A1, A2, · · · , An 为 n 个非空集合,称A1 × A2 × · · · × An 的任意子集 R 为A1, A2, · · · , An 的一个n 元关系(n-ary relation)。
4.3 关系的表示
4.3.1 关系的集合表示
关系是一种特殊的集合,因此集合的两种基本表示法 (枚举法和叙述法),可以用到关系的表示中.
例如
集合 A = {1, 2, 3, 4} 上的整除关系 R 可用枚举法表示为:
R = {< 1, 1 >, < 1, 2 >, < 1, 3 >, < 1, 4 >, < 2, 2 >, < 2, 4 >, < 3, 3 >, < 4, 4 >};
实数集 R 上的“相等”关系 S 可用叙述法表示为:
S = {< x, y > |(x, y ∈ R) ∧ (x = y)}
4.3.2 关系的图形表示 (A≠B)
设 A = {a1, a2, · · · , an},B = {b1, b2, · · · , bm},R 是从 A 到 B 的一个关系.
- 集合中的元素 a1, a2, · · · , an 和b1, b2, · · · , bm 分别作为图中的结点,用“◦”表示
- 如果 < ai, bj >∈ R,则从 ai 到 bj 可用一有向边 ai −→ bj 相连
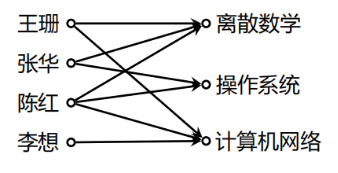
例如:某选课关系 R
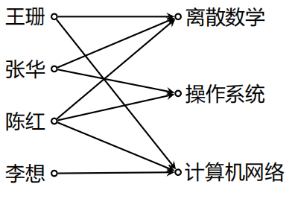
4.3.3 关系的图形表示 (A = B)
设 A = {a1, a2, · · · , an},R 是 A 上的一个关系.
集合中的元素 a1, a2, · · · , an 分别作为图中的结点,用“◦”表示;
如果 < ai, aj >∈ R,则从 ai 到 aj 可用一有向边 ai −→ aj 相连。
如果 < ai, ai >∈ R,则从 ai 到 ai 可用一带箭头的小圆圈表示,即画一个自环
例如:某小于等于关系 R
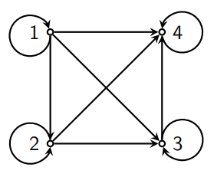
4.3.4 关系的矩阵表示
设 A = {a1, a2, · · · , an},B = {b1, b2, · · · , bm},R 是从 A 到 B 的一个二元关系,称矩阵Mʀ = (m ᵢⱼ)n×m 为关系 R 的关系矩阵(relation matrix),其中(1 ⩽ i ⩽ m,1 ⩽ j ⩽ n)
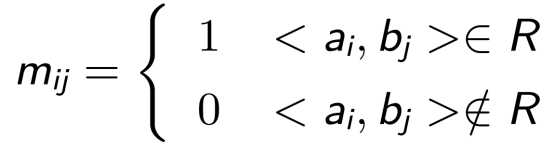
也称Mʀ为 R 的邻接矩阵(adjacency matrix)
例如:某选课关系 R
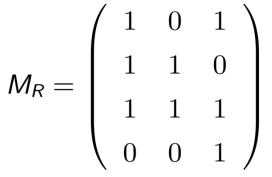
4.3.5 布尔矩阵的并和交运算
如果 A = (aᵢⱼ) 和 B = (bᵢⱼ) 是两个 m × n 矩阵,则A 和 B 的并也是一个 m × n 矩阵,记为A∨B = C = (cᵢⱼ), 其中:
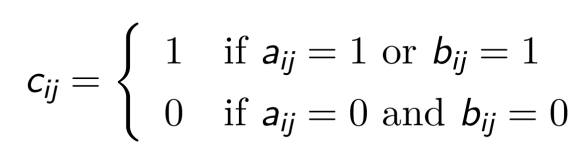
如果 A = (aᵢⱼ) 和 B = (bᵢⱼ) 是两个 m × n 矩阵,则A 和 B 的交也是一个 m × n 矩阵,记为A ∧ B = C = (cᵢⱼ), 其中:
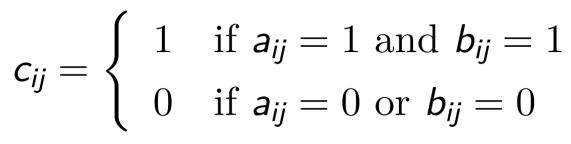
例如

4.3.6 布尔矩阵的积运算
如果 A = (aᵢⱼ) 是m × p矩阵, B = (bᵢⱼ) 是p × n矩阵,则A 和 B 的积是一个m × n矩阵,记为A ⊙ B = C = (cᵢⱼ), 其中:
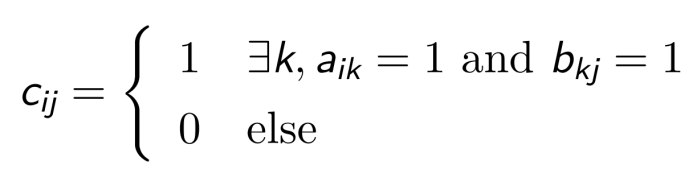
例如
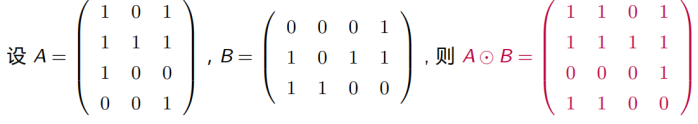
4.4 关系的运算
4.4.1 关系的并交差补运算
关系是一种特殊的集合,因此集合的所有基本运算(并、交、差、补),都可以应用到关系中,并且同样满足集合的所有运算定律.
设 R, S 是从 A 到 B 的两个关系,则

4.4.2 关系的复合运算
设 A, B, C 是三个集合,R 是从 A 到 B 的关系,S 是从 B 到 C 的关系 (即R : A→B, S : B→C),则 R 与 S 的复合关系(合成关系)(composite relation)R ◦ S 是从 A到 C 的关系,并且:
R ◦ S = {< x, z > |(x ∈ A) ∧ (z ∈ C) ∧ (∃y)(y ∈ B ∧ xRy ∧ ySz)}
4.4.3 用三种关系表示法进行复合运算
集合表示法:
寻找所有满足 < x, y >∈ R 并且 < y, z >∈ S, 从而得到< x, z >∈ R ◦ S;
例如
设 A = {a, b, c, d},B = {b, c, d}, C = {a, b, d}, R = {< a, b >, < c, d >, < b, b >} 是 A 到 B 的关
系,S = {< d, b >, < b, d >, < c, a >} 是 B 到 C 的关系。
则 R ◦ S = {< a, d >, < c, b >, < b, d >}。
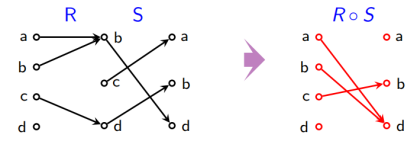
关系图表示法:
将关系 R, S 的关系图画在一起,然后寻找所有首尾相
接的两条有向边,再去掉中间相接的结点 y,可得到 R ◦ S 的关系图
关系矩阵表示法:
直接将关系 R 和 S 的关系矩阵做布尔积运算即得R ◦ S 的关系矩阵
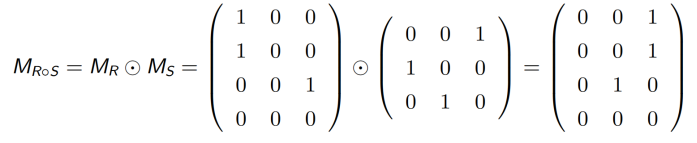
4.4.4 关系的逆运算
设 A, B 是两个集合,R 是 A 到 B 的关系,则从 B 到 A 的关系R⁻¹ = {< b, a > | < a, b >∈ R} 称为 R 的逆关系(inverse relation),运算“⁻¹”称为逆运算(inverse operation)。
由逆运算的定义可知
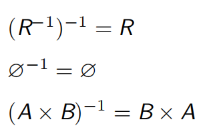
4.4.5 用三种关系表示法求逆
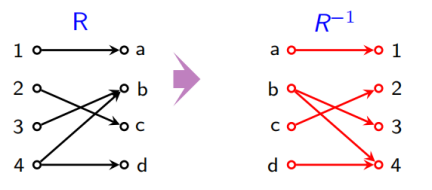
设 A = {1, 2, 3, 4} B = {a, b, c, d},R 是从 A 到 B 的一个关系且R = {< 1, a >, < 2, c >, < 3, b >, < 4, b >, < 4, d >} 则
R⁻¹ = {< a, 1 >, < c, 2 >, < b, 3 >, < b, 4 >, < d, 4 >}
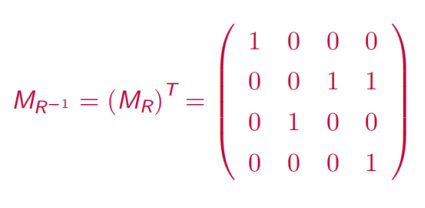
4.5 关系的运算性质
4.5.1 结合律与同一律
设 A、B、C 和 D 是任意四个集合,R、S 和 T 分别是从 A 到 B,B 到 C 和 C 到 D 的二元关
系,Iᴀ 和 Iʙ 分别是 A 和 B 上的恒等关系,则
- (R ◦ S) ◦ T = R ◦ (S ◦ T)
- Iᴀ ◦ R = R ◦ Iʙ = R
4.5.2 分配律
设 A、B、C 和 D 是任意四个集合,R 是从 A 到 B 的关系,S1, S2 是从 B 到 C 的关系,T 是从 C
到 D 的关系,则
- R ◦ (S1 ∪ S2) = (R ◦ S1) ∪ (R ◦ S2)
- R ◦ (S1 ∩ S2) ⊆ (R ◦ S1) ∩ (R ◦ S2)
- (S1 ∪ S2) ◦ T = (S1 ◦ T) ∪ (S2 ◦ T)
- (S1 ∩ S2) ◦ T ⊆ (S1 ◦ T) ∩ (S2 ◦ T)
4.5.3 逆运算
设 A,B, C 是三个集合,R,S 分别是从 A 到 B,从 B 到 C 的关系,则(R ◦ S)⁻¹ = S⁻¹ ◦ R⁻¹
设 R, S 是从集合 A 到集合 B 的关系, 则有
(分配性)
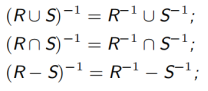
(可换性)
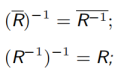
(单调性)
![]()
4.6 关系的幂运算
4.6.1 幂运算的定义
设 R 是集合 A 上的关系,则 R 的 n 次幂,记为 Rⁿ,定义如下:
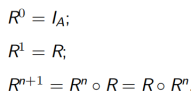
4.6.2 幂运算的收敛性
设 A 是有限集合,且 |A| = n,R 是 A 上的关系,则
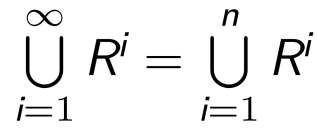
4.7 关系的性质 (一)
4.7.1 自反性与反自反性
设 R 是集合 A 上的关系.
如果对任意的 x ∈ A, 都有 < x, x >∈ R, 那么称 R 在 A 上是自反的(reflexive), 或称R 具有自反性(reflexivity);
例如同姓关系, 小于等于关系, 包含关系, 整除关系都是自反的关系;
如果对任意的 x ∈ A, 都有< x, x >∉R, 那么称R在A上是反自反的(antireflexive),或称R具有反自反性(antireflexivity)
例如父子关系, 小于关系, 真包含关系都是反自反的关系
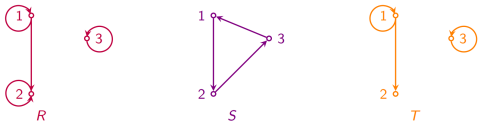
设 A = {1, 2, 3}, 定义 A 上的关系 R, S 和 T 如下:
R = {< 1, 1 >, < 1, 2 >, < 2, 2 >, < 3, 3 >}; 自反
S = {< 1, 2 >, < 2, 3 >, < 3, 1 >}; 反自反
T = {< 1, 1 >, < 1, 2 >, < 1, 3 >, < 3, 1 >, < 3, 3 >}. 非自反, 非反自反
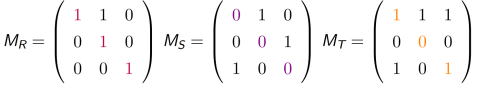
小结
- 存在既不是自反的也不是反自反的关系;
- 关系 R 是自反的当且仅当 R 的关系图中每个结点都有自环, 关系 R 是反自反的当且仅当 R 的关系图中每个结点都无自环;
- 关系 R 是自反的当且仅当 R 的关系矩阵的主对角线上全为 1, 关系 R 是反自反的当且仅当 R 的关系矩阵的主对角线上全为 0
4.7.2 对称性与反对称性
设 R 是集合 A 上的关系.
如果对任意的x, y∈A, 如果< x, y >∈ R, 那么< y, x >∈ R, 则称R是对称的(symmetric), 或称R具有对称性(symmetry);
例如同姓关系, 朋友关系, 同余关系都是对称的关系
如果对任意的x, y∈A, 如果< x, y >∈ R 且< y, x >∈ R,那么x = y, 则称R是反对称的(antisymmetric), 或称R具有反对称性(antisymmetry);
例如小于等于关系, 包含关系, 整除关系都是反对称的关系
设 A = {1, 2, 3, 4}, 定义 A 上的关系 R, S,T 和 V 如下:
R = {< 1, 1 >, < 1, 3 >, < 3, 1 >, < 4, 4 >}; 对称
S = {< 1, 1 >, < 1, 3 >, < 1, 4 >, < 2, 4 >}; 反对称
T = {< 1, 1 >, < 1, 2 >, < 1, 3 >, < 3, 1 >, < 1, 4 >}; 非对称, 非反对称
V = {< 1, 1 >, < 2, 2 >, < 3, 3 >, < 4, 4 >}. 对称, 反对称
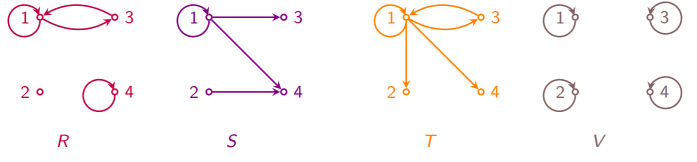
关系图判定法:关系 R 是对称的当且仅当 R 的关系图中, 任何一对结点之间, 要么有方向相反的两条边, 要么无边 ;关系 R 是反对称的当且仅当 R 的关系图中, 任何一对结点之间至多只有一条边。
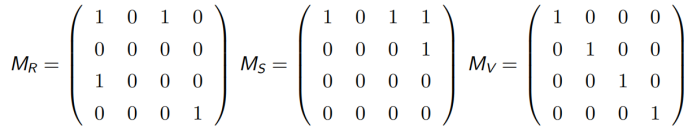
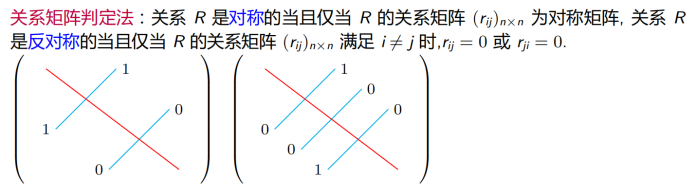
4.7.3 传递性
设 R 是集合 A 上的关系. 对任意的 x, y, z ∈ A, 如果 < x, y >∈ R 且 < y, z >∈ R, 那么< x, z >∈ R, 则称 R 是传递的(transitive), 或称 R 具有传递性(transitivity);
- 同姓关系, 小于关系, 包含关系, 整除关系, 飞机航线的可达关系都是传递的关系;
- 父子关系, 朋友关系, 婚姻关系, 飞机航线的直达关系都不是传递的关系.
设 A = {1, 2, 3}, 定义 A 上的关系 R, S,T 和 V 如下:
R = {< 1, 1 >, < 1, 2 >, < 2, 3 >, < 1, 3 >}; 传递
S = {< 1, 2 >}; 传递
T = {< 1, 1 >, < 1, 2 >, < 2, 3 >}; 非传递
V = {< 1, 2 >, < 2, 3 >, < 1, 3 >, < 2, 1 >}. 非传递
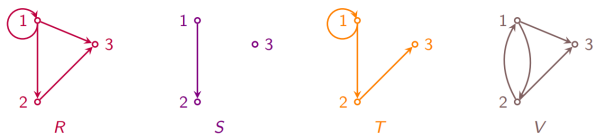
关系 R 是传递的当且仅当在 R 的关系图中, 任何三个不同结点 x, y, z 之间, 若从 x到 y 有一条边存在, 从 y 到 z 有一条边存在, 则从 x 到 z 一定有一条边存在;
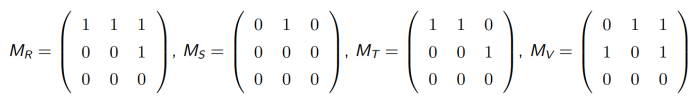

4.8 关系的性质 (二)
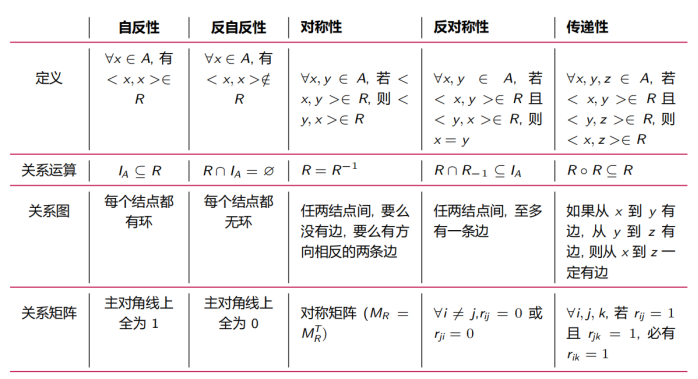
4.8.1 关系性质的判定定理
设 R 是集合 A 上的关系, 则.

4.8.2 关系性质的保守性
设 R, S 是集合 A 上的关系, 则

4.9 关系的闭包
4.9.1 闭包定义
设 R 是集合 A 上的关系, 若存在 A 上的另一个关系 R′, 满足:
- R′ 是自反的 (对称的, 或传递的);
- 对任何自反的 (对称的, 或传递的) 关系 R˝,如果 R ⊆ R˝, 就有 R′ ⊆ R˝
则称 R′ 为 R 的自反闭包(reflexive closure) (对称闭包(symmetric closure), 或传递闭包(transitive closure)), 分别记为r(R)(s(R)或t(R)).
4.9.2 利用关系图求闭包
- 检查关系图,在没有自环的结点处加上自环,可得 r(R) 的关系图;
- 检查关系图,将每条单向边全部改成双向边,可得 s(R) 的关系图;
- 检查关系图,从每个结点出发,找到其终点,如果该结点到终点没有边相连,就加上此边,可得t(R)的关系图
4.9.3 利用关系运算求闭包
设 R 是集合 A 上的关系, 则

![[附源码]SSM计算机毕业设计中小型艺术培训机构管理系统JAVA](https://img-blog.csdnimg.cn/c1c827069c344dc085912cd6c28d1d16.png)



![[附源码]java毕业设计农业种植管理系统](https://img-blog.csdnimg.cn/fac9ad95df2944e7b61f63fb300e7f71.png)





![[附源码]计算机毕业设计JAVA个性化新闻推荐系统](https://img-blog.csdnimg.cn/2e0dea7cabd0413fa13609233dbd31de.png)