基本概念--记忆化DFS

使用数组保存已经算出来的值，在后续的计算中减少大量的重复计算，提高效率。（用于dp不方便，但是搜索方便的情况，可以提升效率。）

eg. 记忆化dfs求解斐波那契数列

int dfs(int n)
{
	if(fib[n]) return n;
	if(n==1 || n==2) fib[n] = 1;
	else fib[n] = (dfs(n-1)+dfs(n-2)) % 1000000007;
	return fib[n];
}

 

经典例题

猫和老鼠

        解：将每一个位置所能得到的最优解都保存在一个二维数组中，每次调用dfs函数时都先判断这个位置的最优解是否曾经已经求出来了，假如求出来了直接返回就行了。

#include <cstdio>
#include <cstring>
using namespace std;

int n, k, init[101][101], ans[101][101];    //init保存每个网格最初奶酪的值，ans保存从当前这个坐标出发能够得到的最优解
int moves[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int dfs(int x, int y);
int max(int x, int y) { return x > y ? x : y; }
bool ok(int x, int y) { return x <= n && y <= n && x > 0 && y > 0; }    //判断是否越界

int main()
{
	while(scanf("%d%d", &n, &k), n != -1 && k!= -1)
	{
		memset(ans, 0, sizeof(ans));
		for(int i = 1; i <= n; i++)
			for(int j = 1; j <= n; j++)
				scanf("%d", &init[i][j]);
		printf("%d\n", dfs(1, 1));
	}
	return 0;
}

int dfs(int x, int y)    //返回从(x,y)出发得到的最优解
{
	int tempMax = 0;
	if(ans[x][y]) return ans[x][y];
	for(int i = 0; i < 4; i++)
		for(int j = 1; j <= k; j++)
		{
			int xx = x + j*moves[i][0];
			int yy = y + j*moves[i][1];
			if(ok(xx, yy) && init[xx][yy] > init[x][y])
				tempMax = max(tempMax, dfs(xx, yy));
		}
	ans[x][y] = init[x][y] + tempMax;
	return ans[x][y];
}

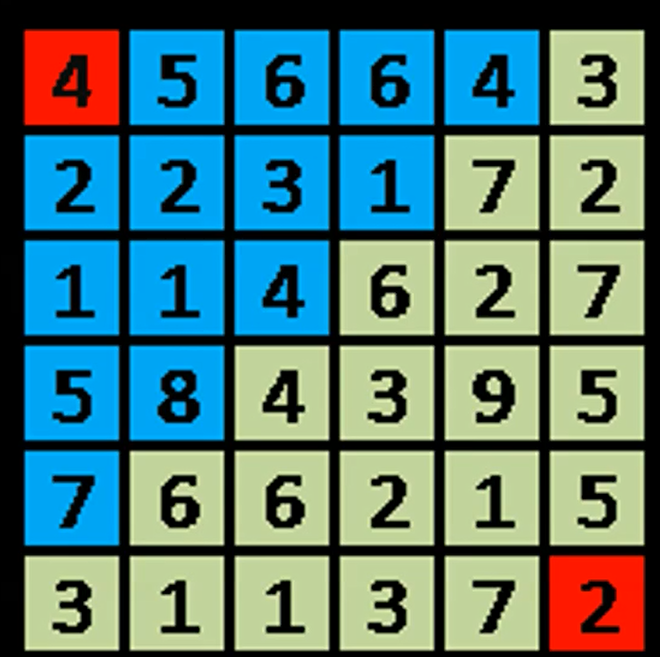
How many ways

        解：假如知道了从蓝色位置走到终点的方案数，那么从左上角（起点）走到终点的方案数也就知道了（所有蓝色方块方案数的和）。

#include <cstdio>
#include <cstring>
using namespace std;

int n, m, t, map[101][101], ans[101][101];
int ok(int x, int y){ return x <= n && y <= m && x > 0 && y > 0; }
int dfs(int, int);

int main()
{
	scanf("%d", &t);
	while(t--)
	{
		scanf("%d%d", &n, &m);
		memset(ans, -1, sizeof(ans));
		for(int i = 1; i <= n; i++)
			for(int j = 1; j <= m; j++)
				scanf("%d", &map[i][j]);
		ans[n][m] = 1;
		printf("%d\n", dfs(1, 1));
	}
	return 0;
}

int dfs(int x, int y)
{
	if(ans[x][y] > -1) return ans[x][y];
	ans[x][y] = 0;
	for(int i = 0; i <= map[x][y]; i++)
		for(int j = 0; j <= map[x][y]-i; j++)
			if(ok(x+i, y+j))
				ans[x][y] = (dfs(x+i, y+j)+ans[x][y]) % 10000;
	return ans[x][y];
}

 

基本概念--基于优先队列的BFS

优先队列（priority_queue）：

1. 在队尾加入元素
2. 在队头删除元素
3. 每次取出的时具有最高优先权的元素

基本用法：

创建队列对象：priority_queue<元素类型> 队列名;

队列添加元素：队列名.push(元素名);

去掉最优元素：队列名.pop();

判断是否为空：队列名.empty();

返回队列大小：队列名.size();

访问最优元素：队列名.top();

假如需要对结构体数组定义“优先权”，那么就要重载运算符

eg. 保存三个整数的结构体，从前往后依次比较三个整数，从小往大排。

struct T
{
    int x, y, z;
    friend bool operater < (T t1, T t2)
    {
        if(t1.x != t2.x) return t1.x > t2.x;
        if(t1.y != t2.y) return t1.y > t2.y;
        return t1.z > t2.z;
    }
};

 

经典例题

拯救丁爸

        解：前来拯救的学生有多个时，可以反向思考（丁爸找学生的位置）。

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
int n, m, ans;
char map[201][201]; 
int mintime[201][201];
int dir[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};

struct state {
    int x, y, ti; 
    friend bool operator < (state s1,state s2)
    {
        return s2.ti < s1.ti;
    }
};

state be;

bool in(int x, int y) { return x >= 1 && y >= 1 && x <= n && y <= m && map[x][y] != '#'; }

int bfs() 
{
    priority_queue<state> q;
    q.push(be);
    state cur, next;
    while (!q.empty()) 
	{
        cur = q.top();
        mintime[cur.x][cur.y] = 1;
        if (map[cur.x][cur.y] == 'r') return cur.ti;
        q.pop();
        for (int i = 0; i < 4; i++) 
		{
            next.x = cur.x + dir[i][0];
            next.y = cur.y + dir[i][1];
            if (in(next.x, next.y)) 
			{
                next.ti = cur.ti+1;
                if (map[next.x][next.y] == 'x') next.ti++;
                if(!mintime[next.x][next.y])
                {
                    q.push(next);
                    mintime[next.x][next.y] = 1;
                }
            }
        }
    }
    return 0;
}

int main() 
{
    while (cin >> n >> m) 
	{
        ans = 0; 
		memset(mintime, 0, sizeof(mintime));
        for (int i = 1; i <= n; i++) 
		{
            for (int j = 1; j <= m; j++) 
			{
                cin >> map[i][j];
                if (map[i][j] == 'a') 
				{
                    be.x = i; 
					be.y = j;
                    be.ti = 0;
                }
            }
        }
        int t = bfs();
        if(t) cout << t << endl;
        else cout << "Poor Dingba has to stay in the prison all his life." << endl;
    }
}

哈夫曼编码

概念

• 路径：由一个节点到另一个节点间的分支构成
• 路径长度：路径上经过的分支数量
• 树的路径长度：从树根到每一节点的路径长度之和
• 带权路径长度：节点到根的路径长度与节点上权重的乘积
• 树的带权路径长度：树中所有叶子节点的带权路径长度之和，（Weighted Path Length）
• 哈夫曼树：带权路径长度最小的树

作用：在发送报文时可以构造最少的01序列来表示所有字母。

特点：每一个码都不是另一个码的前缀，称为前缀码。（所以发电报的时候才不会产生歧义。）

解：每次在优先队列中找两个最小的数，把它们的和插入优先队列。如此往复就可以得到一个哈夫曼树。

#include <iostream>
#include <string>
#include <cstring>
#include <queue>
using namespace std;

string str;
int num[27];
int bfs();

int main()
{
	while(cin >> str, str != "END")
	{
		memset(num, 0, sizeof(num));
		int len = str.size();
		for(int i = 0; i < len; i++)
		{
			if(str[i] == '_') num[26]++;
			else num[str[i]-'A']++;
		}
		int res = bfs();
		printf("%d %d %.1f\n", len*8, res, len*8*1.0/res);
	}
	return 0;
}

int bfs()
{
	int a, b, sum=0;
	priority_queue<int, vector<int>, greater<int> > Q;
	for(int i = 0; i <= 26; i++)
		if(num[i]) Q.push(num[i]);
	if(Q.size() == 1) sum = Q.top();
	while(Q.size() > 1)
	{
		a = Q.top();
		Q.pop();
		b = Q.top();
		Q.pop();
		sum += a + b;
		Q.push(a+b);
	}
	return sum;
}