69. x 的平方根
给你一个非负整数
x,计算并返回x的 算术平方根 。由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如
pow(x, 0.5)或者x ** 0.5。示例 1:
输入:x = 4 输出:2
示例 2:
输入:x = 8 输出:2 解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
提示:
0 <= x <= 2^31-1
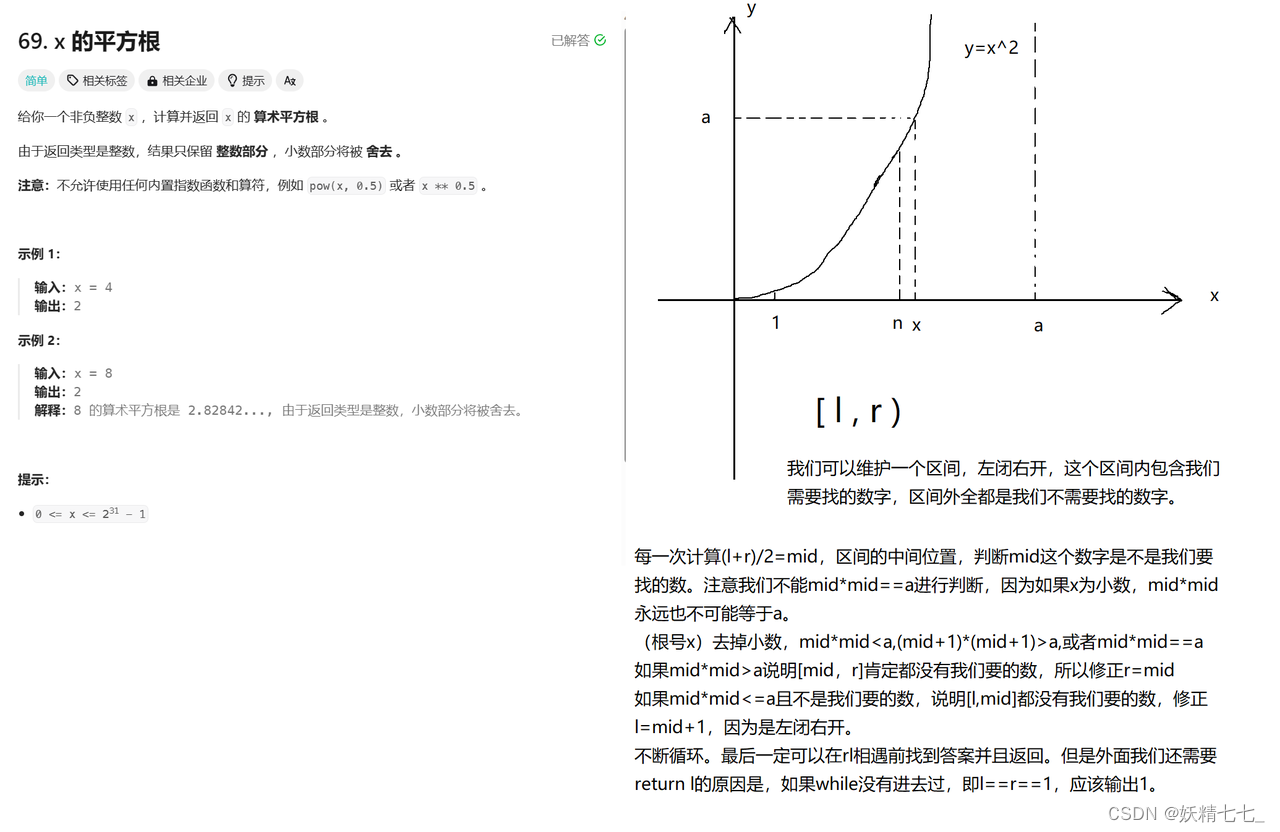
二分查找:
int mySqrt(long long a) {
if (a == 0)
return a;
long l = 1, r = a, mid;
while (l < r) {
mid = l + (r - l) / 2;
if (mid * mid < a && (mid + 1) * (mid + 1) > a || mid * mid == a) {
return mid;
} else if (mid * mid > a) {
r = mid;
} else {
l = mid + 1;
}
}
return r;
}int mySqrt(long long a) {这行定义了函数 mySqrt,它接受一个 long long 类型的参数 a,表示要求平方根的数字。返回类型是 int,意味着返回的是 a 的平方根的整数部分。
if (a == 0) return a;这里检查 a 是否等于 0,如果是,则直接返回 0。这是因为 0 的平方根是 0,这个条件判断帮助我们提前处理边界情况。
long l = 1, r = a, mid;这行初始化了三个变量,l(左边界)被初始化为 1,r(右边界)被初始化为 a,mid 用于存储中间值。这是二分查找算法的初始设置,用于在 1 到 a 之间找到平方根的整数部分。注意我们寻找的区间是[l,r)左闭右开,一直维护这个区间并且不断地缩小区间。
while (l < r) {这个 while 循环将会继续执行,直到左边界 l 不再小于右边界 r。这个循环是二分查找的核心,用于缩小查找范围。
mid = l + (r - l) / 2;在每次循环中,我们计算 l 和 r 之间的中点 mid。这种计算方式可以防止 (l + r) 直接相加时可能出现的整数溢出。
if (mid * mid < a && (mid + 1) * (mid + 1) > a || mid * mid == a) { return mid; }这个 if 语句检查 mid 的平方是否恰好等于 a,或者 mid 的平方小于 a 但 (mid + 1) 的平方大于 a。如果满足这些条件之一,那么 mid 就是 a 的平方根的整数部分,函数返回 mid。
else if (mid * mid > a) { r = mid; }如果 mid 的平方大于 a,说明平方根在 l 和 mid 之间,所以我们把右边界更新为 mid。
else { l = mid + 1; }如果 mid 的平方小于 a,说明平方根在 (mid + 1) 和 r 之间,所以我们把左边界更新为 mid + 1。
时间复杂度和空间复杂度分析
时间复杂度: O(log a)。因为这是一个二分查找算法,每次循环都将搜索范围减半,所以时间复杂度是对数级别的。
空间复杂度: O(1)。我们只使用了有限的几个变量,所以空间复杂度是常数级别的。
牛顿迭代法:
int mySqrt(int a) {
long x = a;
while (x * x > a) {
x = (x + a / x) / 2;
}
return x;
}
int mySqrt(int a) {这行定义了一个名为 mySqrt 的函数,它接受一个 int 类型的参数 a,表示要求平方根的数字。返回类型也是 int,表示返回的是 a 的平方根的整数部分。
long x = a;这里,我们首先将输入的 int 类型的 a 转换成 long 类型并赋值给变量 x。这样做主要是为了防止在后面的计算中可能出现的溢出问题。选择 long 类型是因为它的范围比 int 类型更大,可以处理更大的数。
while (x * x > a) {这个 while 循环的条件是 x * x 大于 a,意味着只要 x 的平方还大于 a,就继续迭代。牛顿迭代法的核心思想是逐渐逼近真实的根,所以这个条件确保了我们只在还没有找到合适的平方根时继续迭代。
x = (x + a / x) / 2;这行是牛顿迭代法的迭代公式推导得到的公式。
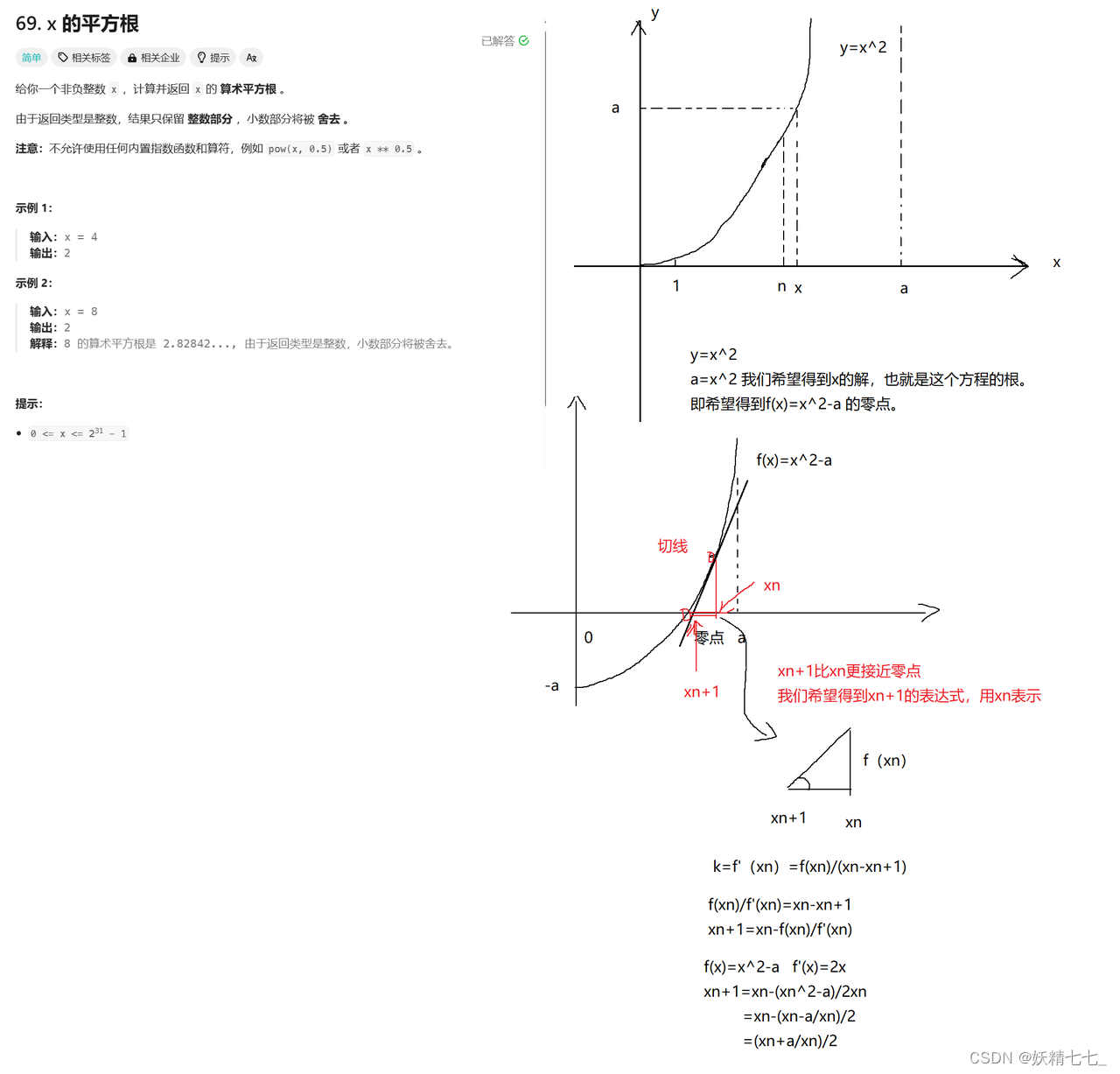
牛顿迭代法的基本原理
假设我们要找的方程是 $$f(x) = 0$$,并且我们已经有了一个近似解 $$x_n$$。牛顿迭代法的下一个近似解 $$x_{n+1}$$可以通过下面的公式计算得到:$$ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} $$
这里, $$f'(x_n)$$ 表示 $$f(x)$$在 $$x_n $$处的导数。直观上,这个公式通过当前估计点的函数值和斜率来找到函数图形与x轴的交点,这个交点就是新的估计根。
当 while 循环结束,说明我们找到了满足 x * x <= a 的最大的 x 值,这个 x 就是 a 的平方根的整数部分,函数返回这个值。
时间复杂度和空间复杂度分析
时间复杂度: O(log a)。虽然这看起来是一个简单的迭代,但牛顿迭代法的收敛速度非常快,通常被认为具有对数时间复杂度。
空间复杂度: O(1)。我们只使用了有限的几个变量进行计算,因此空间复杂度是常数级别的。
34. 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组
nums,和一个目标值target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值
target,返回[-1, -1]。你必须设计并实现时间复杂度为
O(log n)的算法解决此问题。示例 1:
输入:nums = [5,7,7,8,8,10], target = 8 输出:[3,4]示例 2:
输入:nums = [5,7,7,8,8,10], target = 6 输出:[-1,-1]示例 3:
输入:nums = [], target = 0 输出:[-1,-1]
提示:
0 <= nums.length <= 10(5)
-10(9) <= nums[i] <= 10(9)
nums是一个非递减数组
-10(9) <= target <= 10(9)
class Solution {
public:
// 辅函数
int lower_bound(vector<int>& nums, int target) { // 小于 大于等于
int l = 0, r = nums.size() - 1, mid;
while (l < r) {
mid = (l + r) / 2;
if (nums[mid] >= target) {
r = mid;
} else {
l = mid + 1;
}
}
return l;
}
// 辅函数
int upper_bound(vector<int>& nums, int target) { // 小于等于 大于
int l = 0, r = nums.size() - 1, mid;
while (l < r) {
mid = (l + r + 1) / 2;
if (nums[mid] > target) {
r = mid - 1;
} else {
l = mid;
}
}
return l;
}
// 主函数
vector<int> searchRange(vector<int>& nums, int target) {
if (nums.empty())
return vector<int>{-1, -1};
int lower = lower_bound(nums, target);
int upper = upper_bound(nums, target);
if (nums[lower] != target) {
return vector<int>{-1, -1};
}
return vector<int>{lower, upper};
}
};

辅助函数lower_bound解析
int lower_bound(vector<int>& nums, int target) {这是lower_bound函数的定义,它接收一个整数数组nums和一个整数target作为参数,目标是找到第一个不小于target的元素的索引。
int l = 0, r = nums.size() - 1, mid;定义了三个整数变量l、r和mid,分别表示搜索范围的左边界、右边界和中点。初始化l为0,r为nums.size() - 1,因为是闭区间搜索。
while (l < r) { mid = (l + r) / 2; if (nums[mid] >= target) { r = mid; } else { l = mid + 1; } }这段循环通过不断地调整l和r的值来缩小搜索范围,最终目的是找到第一个不小于target的元素。这里采用的是二分查找算法,可以高效地定位元素。不断地维护区间[l,r]的意义,并且不断地缩小区间直至区间大小为1。[l,r]的意义是大于等于target,前面都是小于target的数,后面都是大于等于target的数。如果r是等于mid,r不会改变,所以不能选择右侧为最后的判断项,所以mid的计算不需要加1。
return l; }返回左边界l,这时l即为第一个不小于target的元素的索引。
辅助函数upper_bound解析
int upper_bound(vector<int>& nums, int target) {定义upper_bound函数,其目的是找到最后一个等于target的元素的索引。
int l = 0, r = nums.size() - 1, mid;与lower_bound函数类似,定义搜索范围的左边界l、右边界r以及中点mid。
while (l < r) { mid = (l + r + 1) / 2; if (nums[mid] > target) { r = mid - 1; } else { l = mid; } }这个循环是为了找到最后一个等于target的元素。与lower_bound不同的是,这里在计算mid时加了1,并且调整r的策略也略有不同,以确保可以正确处理边界情况。不断地维护区间[l,r]的意义,并且不断地缩小区间直至区间大小为1。[l,r]的意义是小于等于target,前面都是小于等于target的数,后面都是大于target的数。如果l是等于mid,l不会改变,所以不能选择左侧为最后的判断项,所以mid的计算需要加1。
return l; }返回左边界l,此时l指向第一个大于target的元素的索引。
主函数searchRange解析
vector<int> searchRange(vector<int>& nums, int target) {这是主函数的定义,它接收一个整数数组nums和一个整数target,返回一个包含两个整数的数组,代表target的起始和结束位置。
if (nums.empty()) return vector<int>{-1, -1};如果输入数组为空,则直接返回{-1, -1},表示找不到target。
int lower = lower_bound(nums, target); int upper = upper_bound(nums, target);调用lower_bound和upper_bound函数找到target的下界和上界。
if (nums[lower] != target) { return vector<int>{-1, -1}; }如果lower位置的元素不是target,说明target不在数组中,返回{-1, -1}。
return vector<int>{lower, upper}; 返回一个临时对象。 }如果找到了target,返回其起始和结束位置的索引。
时间复杂度和空间复杂度分析
时间复杂度:这两个辅助函数以及主函数都使用了二分查找,所以时间复杂度为O(log n)。
空间复杂度:没有使用额外的空间(除了输入和返回的数组外),所以空间复杂度为O(1)。
81. 搜索旋转排序数组 II
已知存在一个按非降序排列的整数数组
nums,数组中的值不必互不相同。在传递给函数之前,
nums在预先未知的某个下标k(0 <= k < nums.length)上进行了 旋转 ,使数组变为[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如,[0,1,2,4,4,4,5,6,6,7]在下标5处经旋转后可能变为[4,5,6,6,7,0,1,2,4,4]。给你 旋转后 的数组
nums和一个整数target,请你编写一个函数来判断给定的目标值是否存在于数组中。如果nums中存在这个目标值target,则返回true,否则返回false。你必须尽可能减少整个操作步骤。
示例 1:
输入:nums = [2,5,6,0,0,1,2], target = 0 输出:true示例 2:
输入:nums = [2,5,6,0,0,1,2], target = 3 输出:false提示:
1 <= nums.length <= 5000
-10(4) <= nums[i] <= 10(4)题目数据保证
nums在预先未知的某个下标上进行了旋转
-10(4) <= target <= 10(4)进阶:
这是 搜索旋转排序数组 的延伸题目,本题中的
nums可能包含重复元素。这会影响到程序的时间复杂度吗?会有怎样的影响,为什么?
bool search(vector<int>& nums, int target) {
int start = 0, end = nums.size() - 1;
while (start <= end) {
int mid = (start + end) / 2;
if (nums[mid] == target) {
return true;
}
if (nums[start] == nums[mid]) {
// 无法判断哪个区间是增序的
++start;
} else if (nums[mid] <= nums[end]) {
// 右区间是增序的
if (target >= nums[mid] && target <= nums[end]) {
start = mid;
} else {
end = mid - 1;
}
} else {
// 左区间是增序的
if (target >= nums[start] && target <= nums[mid]) {
end = mid;
} else {
start = mid + 1;
}
}
}
return false;
}
bool search(vector<int>& nums, int target) {定义了一个名为search的函数,它接受一个整数数组nums和一个整数target作为参数,并返回一个布尔值。这个布尔值表示target是否存在于nums中。
int start = 0, end = nums.size() - 1;定义了两个整数start和end作为搜索的起始和结束位置,分别初始化为0和nums.size() - 1。
while (start <= end) {这是一个循环,条件是start小于等于end。循环的目的是在nums中查找target,直到找到target或start大于end。
int mid = (start + end) / 2;计算中点mid的位置,用于分割数组并决定下一步搜索的方向。
if (nums[mid] == target) { return true; }如果在mid位置找到了target,则函数返回true。
if (nums[start] == nums[mid]) { // 无法判断哪个区间是增序的 ++start; }如果start位置和mid位置的元素相等,无法判断哪个区间是有序的,所以将start向前移动一位,以缩小搜索范围。
else if (nums[mid] <= nums[end]) { // 右区间是增序的 if (target >= nums[mid] && target <= nums[end]) { start = mid; } else { end = mid - 1; } }如果mid位置的元素小于等于end位置的元素,说明右区间是有序的。然后判断target是否在这个有序的右区间内。如果是,调整start到mid;如果不是,调整end到mid - 1。
else { // 左区间是增序的 if (target >= nums[start] && target <= nums[mid]) { end = mid; } else { start = mid + 1; } }如果上述条件都不满足,说明左区间是有序的。接着判断target是否在这个有序的左区间内。如果是,调整end到mid;如果不是,调整start到mid + 1。
return false; }如果循环结束还没有找到target,则返回false,表示target不在nums中。
时间复杂度和空间复杂度分析
时间复杂度:O(log n)。虽然存在一些特殊情况(如nums[start] == nums[mid]时只能逐个检查),大多数情况下该算法能够以对数时间复杂度运行,因为它每次都将搜索范围减半。
空间复杂度:O(1)。该算法只使用了固定数量的额外空间(几个整型变量),因此空间复杂度是常数级别的。
结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!