数据结构与算法第四套试卷（青科大）

news2024/11/16 18:08:45

1.图

无向图入度=出度之和
所有入度之和为=2*边数

2.树

**知识点：**注意二叉排序树！=深度平衡树，所以可能会出现极端现象（链表），时间复杂度为0(n)，如果为最好情况即为0(logn)

3.图

1.邻接表n个表头节点则说明图有n个顶点，m个表节点说明图有m条边（有向图）
2.无向图在邻接矩阵中是对称的
在这里插入图片描述
解： A[i][j]=1

4.双向链表删除节点

在这里插入图片描述
1.p->llink->rlink=p->rlink;
2.p->rlink->llink=p->llink;

5.高度

log2n+1;

6.完全二叉树

高度为h的节点范围为：2^(h-1)-1+1=2的h-1次方~2的h次方-1

7.建堆

第一个元素建堆必须从n/2开始建
在这里插入图片描述

8.哈夫曼树

介绍： 不断合并权值较小的两棵树来生成新的树，直至所有的元素合并成一棵树为止，每次合并都会生成一个新的内部节点，其权值为两个子树权值之和，直到最终形成一棵完整的哈夫曼树。

特殊之处： 只有n0和n2的节点，所以n=n0+n2=2n0-1；所以n0为50，99个节点的哈夫曼树一共有50个叶子节点；

9.二叉链

对于n个节点的二叉树有2n个指针域，一共n-1个非空指针域，n+1个空指针域，所以99个节点，一共有198个指针域，非空有98个，空指针域一共有100个；

10.循环队列

当一个循环队列有m个存储单元，则循环队列最多能够存储m-1个元素；反之，若一个循环队列能够存储m-1个元素，则循环队列至少有m个存储单元

11.小根堆的构造

与大根堆类似，就是小的元素当根节点去了；
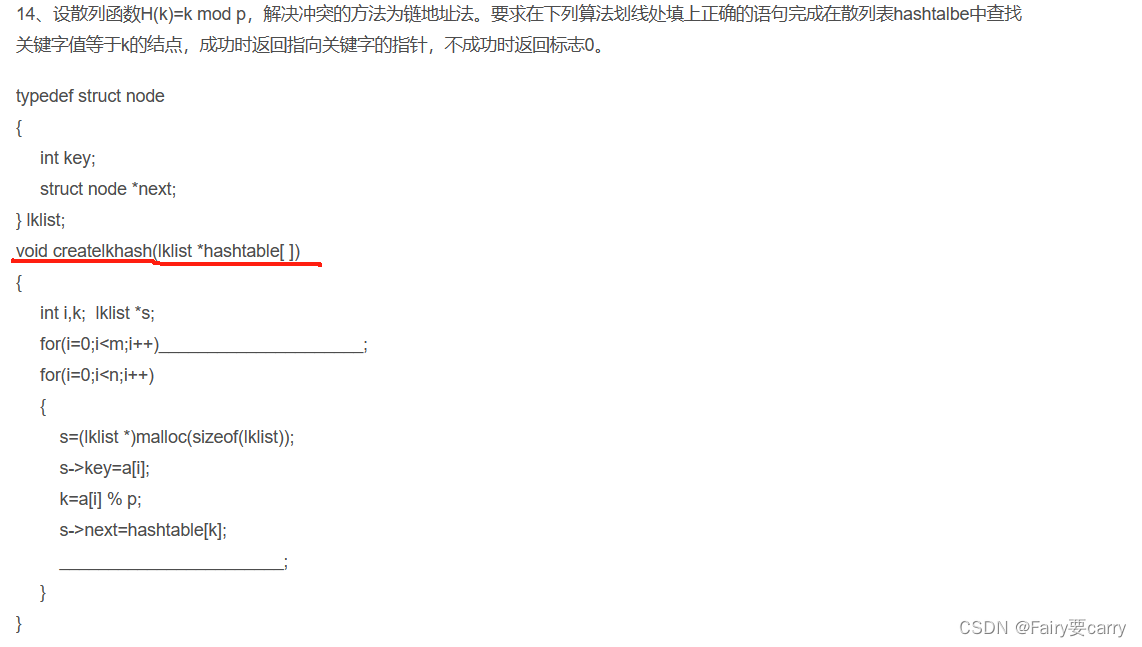
在这里插入图片描述
小根堆的构造：
请添加图片描述

12.树的遍历

在这里插入图片描述

13.链地址法：

在这里插入图片描述
第一空： hashtable[i]=NULL； (初始化散列表每个位置的指针指向为空)
第二空： hashtable[k]=s；将新节点s插入到散列表中位置k处的链表头部
s->next=hashtable[k]的原因：
目的是将新节点s的next指针指向散列表hashtable中位置k处的链表头部
在链地址法中，如果多个关键字映射到同一个位置，可以采用链表解决，当要插入新节点s时，完美为了确保 新节点能够连接到链表的头部，故将新节点s的next指针指向当前k位置的来年表头部——>使新节点s成为的链表头部；

大题：

1.广义表

在这里插入图片描述
1.表头： (a)
2.表尾:（记得多部分时，需要加个括号） (((b),c),(((d))))；
3.长度：（数逗号区分开来的部分个数即可） 3个
4.深度： 数最多括号数即可——>4个

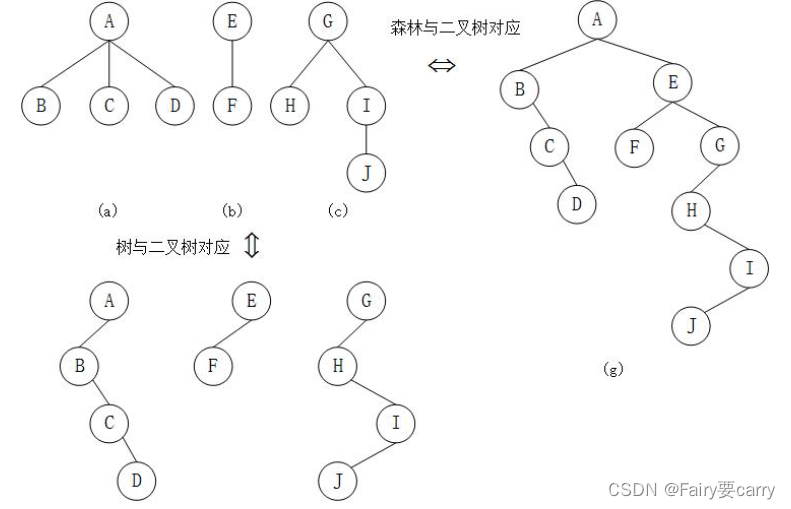
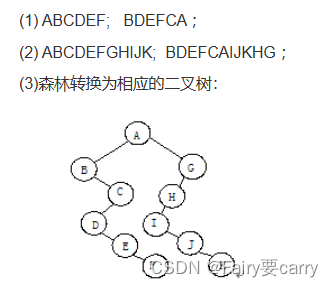
2.森林和二叉树：

森林转二叉树：
主要抓住一个思想，左孩子右兄弟；
森林的遍历，前序遍历等于二叉树的前序遍历，中序遍历等于二叉树的后序遍历
在这里插入图片描述

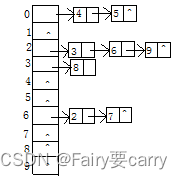
3.散列法

一般取质数（素数）
在这里插入图片描述
H(4)=H(5)=0,H(3)=H(6)=H(9)=2,H(8)=3,H(2)=H(7)=6
请添加图片描述

4.交换二叉树上所有节点左右子树

typedef struct Node{
  int data;
  struct Node* lchild,*rchild;
}BiTree;

void swapTree(BiTree *head){
   //1.BASE
   if(head==NULL) return;
   //2.递归到左右子树节点
   BiTree* left=swapTree(head->lchild);
   BiTree* right=swapTree(head->rchild);
   //3.交换
   root->left=right;
   root->right=left;
}

5.分类链表

设单链表中有仅三类字符的数据元素(大写字母、数字和其它字符)，要求利用原单链表中结点空间设计出三个单链表的算法，使
每个单链表只包含同类字符

#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
    char data;
    struct Node* next;
} Node;

void splitLinkedList(Node* head, Node** uppercaseList, Node** digitList, Node** otherList) {
    Node *current = head;
    Node *upperHead = NULL, *digitHead = NULL, *otherHead = NULL;
    
    Node *upperTail = NULL, *digitTail = NULL, *otherTail = NULL;
    
    while (current != NULL) {
        Node *temp = current->next;
        
        if ((current->data >= 'A' && current->data <= 'Z')) { // 大写字母
            if (upperHead == NULL) {
                upperHead = current;
                upperTail = current;
                current->next = NULL;
            } else {
                upperTail->next = current;
                upperTail = current;
                current->next = NULL;
            }
        } else if ((current->data >= '0' && current->data <= '9')) { // 数字
            if (digitHead == NULL) {
                digitHead = current;
                digitTail = current;
                current->next = NULL;
            } else {
                digitTail->next = current;
                digitTail = current;
                current->next = NULL;
            }
        } else { // 其他字符
            if (otherHead == NULL) {
                otherHead = current;
                otherTail = current;
                current->next = NULL;
            } else {
                otherTail->next = current;
                otherTail = current;
                current->next = NULL;
            }
        }
        
        current = temp;
    }
    
    *uppercaseList = upperHead;
    *digitList = digitHead;
    *otherList = otherHead;
}

// 示例函数，打印单链表中的元素
void printLinkedList(Node* head) {
    Node* current = head;
    while (current != NULL) {
        printf("%c -> ", current->data);
        current = current->next;
    }
    printf("NULL\n");
}