给你一棵二叉树，请你返回满足以下条件的所有节点的值之和：

该节点的祖父节点的值为偶数。（一个节点的祖父节点是指该节点的父节点的父节点。）
如果不存在祖父节点值为偶数的节点，那么返回 0 。

示例：

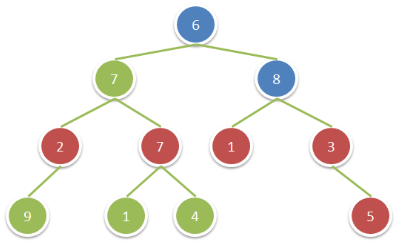
输入：root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]
输出：18
解释：图中红色节点的祖父节点的值为偶数，蓝色节点为这些红色节点的祖父节点。

提示：

树中节点的数目在 1 到 10^4 之间。
每个节点的值在 1 到 100 之间。

法一：直接递归模拟即可：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumEvenGrandparent(TreeNode* root) {
        int ans = 0;
        findAns(root, false, false, ans);
        return ans;
    }

private:
    void findAns(TreeNode *node, bool isEvenFather, bool isEvenGrandFather, int &ans)
    {
        if (node == nullptr)
        {
            return;
        }

        if (isEvenGrandFather)
        {
            ans += node->val;
        }
        findAns(node->left, !(node->val & 1), isEvenFather, ans);
        findAns(node->right, !(node->val & 1), isEvenFather, ans);
    }
};

如果树中有n个节点，此算法时间复杂度为O(n)，空间复杂度为O(logn)。

法二：广度优先搜索，每遍历到一个偶数节点，将其孙子节点的值加上：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumEvenGrandparent(TreeNode* root) {
        queue<TreeNode *> q;
        q.push(root);
        int ans = 0;
        while (!q.empty())
        {
            TreeNode *node = q.front();
            q.pop();
            if (!(node->val & 1))
            {
                if (node->left)
                {
                    if (node->left->left)
                    {
                        ans += node->left->left->val;
                    }

                    if (node->left->right)
                    {
                        ans += node->left->right->val;
                    }
                }

                if (node->right)
                {
                    if (node->right->left)
                    {
                        ans += node->right->left->val;
                    }

                    if (node->right->right)
                    {
                        ans += node->right->right->val;
                    }
                }
            }

            if (node->left)
            {
                q.push(node->left);
            }

            if (node->right)
            {
                q.push(node->right);
            }
        }

        return ans;
    }
};

如果树中有n个节点，此算法时间复杂度为O(n)，空间复杂度为O(logn)。