欢迎来看博主的算法讲解
博主ID:代码小豪
文章目录
- 逆波兰表达式
- 逆波兰表达式的作用
- 代码
- 将中缀表达式转换成后缀表达式
- 文末代码
逆波兰表达式
先来看看leetcode当中的原题

大多数人初见逆波兰表达式的时候大都一脸懵逼,因为与平时常见的表达式不同,很难将常见的表达式与逆波兰表达式联系在一次。
比如:
常见表达式(中缀表达式):((2 + 1) * 3) = 9。
其逆波兰表达式为(后缀表达式):2 1+ 3 *
再解决这个问题之前,首先我们先来了解一下为什么要用逆波兰表达式,而不是中缀表达式呢?
逆波兰表达式的作用
对于人来说,中缀表达式显然是通俗易懂的,但是如果让计算机来处理输入的中缀表达式呢?大家可以想想该如何实现。
显而易见,计算机处理输入的中缀表达式是较为麻烦的。为了解决让计算机便于进行四则运算,逆波兰表达式被发明出来了。
逆波兰表达式的计算方式如下:
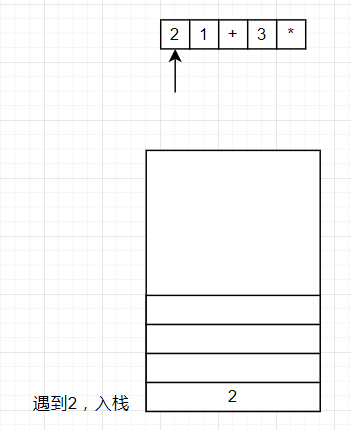
将逆波兰表达式从头开始遍历,如果遇到数字,就将数字压入栈中,如果遇到符号,就将栈顶的两个数字弹出,并将计算结果压入栈中。
以:2 1+ 3 *
为例
将2,1压入栈中,遇到+,将1,2弹出,1+2=3,将计算结果的3压入栈中。接着再将3压入栈中,遇到*将3,3弹出,3*3=9,最终结果为9.
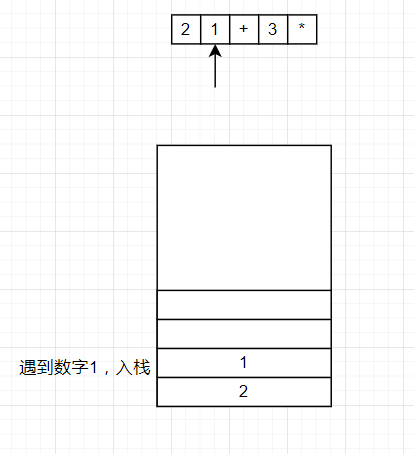
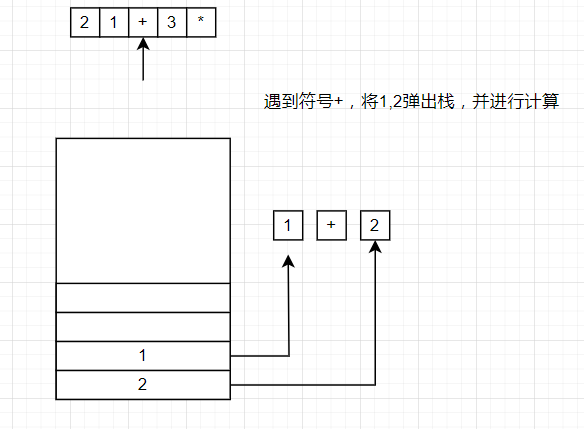
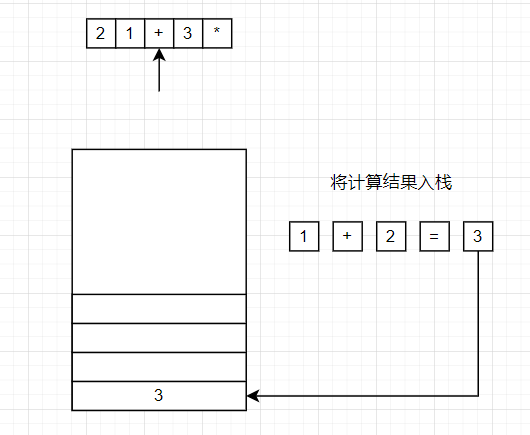
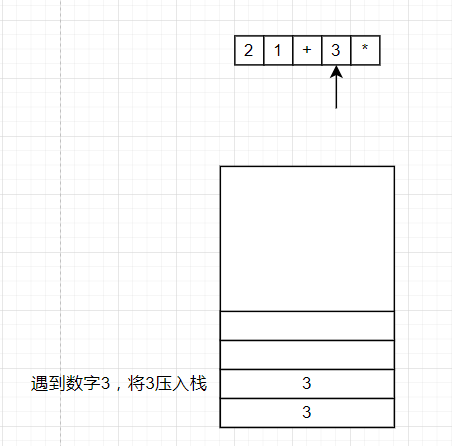
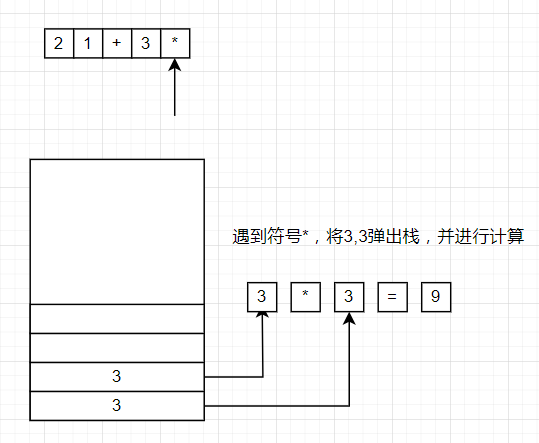
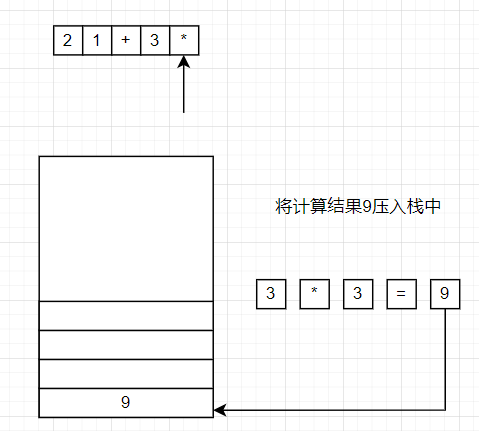
通过了解后缀表达式的计算方法后,可以发现后缀表达式可以通过栈操作来计算出来,这也是计算机中常见的存储结构之一。这就是逆波兰表达式的意义。
既然已经知道了逆波兰表达式的计算方法,那么完成这道题就不难了。
代码
//以下是栈的操作函数
typedef int datatype;
typedef struct stack
{
datatype* data;
int capacity;
int top;
}stack;
void StackInit(stack* ps);//将栈进行初始化
void StackDestory(stack* ps);//释放栈空间
void StackPush(stack* ps, datatype n);//压栈操作
void StackPop(stack* ps);//出栈操作
datatype StackTopData(stack* ps);//获取栈顶
bool StackEmpty(stack* ps);//判断栈是否为空
//逆波兰表达式的函数
int evalRPN(char** tokens, int tokensSize) {
stack* rpn = malloc(sizeof(stack));
StackInit(rpn);//初始化栈空间
int ret = 0;
while (tokensSize--)//遍历整个后缀表达式
{
if (**tokens == '+' ||//判断符号
**tokens == '-' ||
**tokens == '*' ||
**tokens == '/')
{
if (strlen(*tokens) == 1)//由于测试案例中有“-1”这种特殊字符串,因此设计的判断条件。
{
int num1 = StackTopData(rpn);
StackPop(rpn);
int num2 = StackTopData(rpn);
StackPop(rpn);
switch (**tokens)
{
case '+':StackPush(rpn, num2 + num1);
break;
case'-':StackPush(rpn, num2 - num1);
break;
case'*':StackPush(rpn, num2 * num1);
break;
case'/':StackPush(rpn, num2 / num1);
break;
}
}
else {
int num = 0;
num = atoi(*tokens);
StackPush(rpn, num);
}
}
else
{
int num = 0;
num = atoi(*tokens);//将字符转换成整型数据(库函数)
StackPush(rpn, num);
}
tokens++;
}
ret = StackTopData(rpn);//将计算结果弹出栈
StackDestory(rpn);
return ret;//返回计算结果
}
(为了节省篇幅,将栈的相关操作的函数定义进行省略,如果想要完整版代码,可以再文章末尾查看)
将中缀表达式转换成后缀表达式
力扣当中的原题直接将后缀表达式作为输入,因此在完成这道题时并不需要考虑将中缀表达式转换成后缀表达式。
后缀表达式是为了让计算机能用栈来处理四则运算,所以后缀表达式的主要作用是按照顺序来,展示中缀表达式的优先级。
比如:2 1+ 3 *
其中缀表达式为(2+1)*3
()的优先级高于*,因此先将优先级高的数字进行计算,即(2+1),。接着计算*3,因此总体的计算方式为2+1,接着*3,为了满足前边所讲的栈操作,因此应该写为2 1 +(先算2+1)。然后3*,总体上为2 1 + 3 *.
将中缀表达式转换成后缀表达式的过程也可以用栈来实现,原理如下:
建立一个栈,用于压入符号。遇到数字直接输出就行。
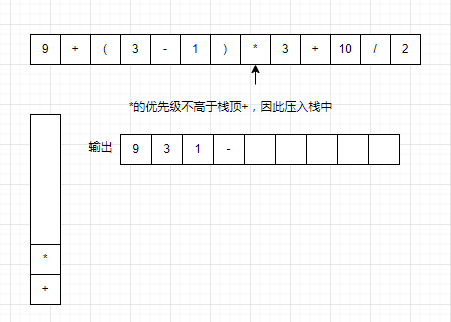
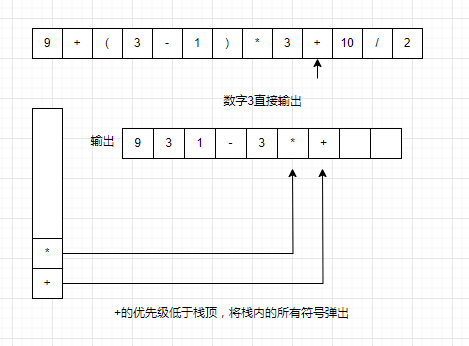
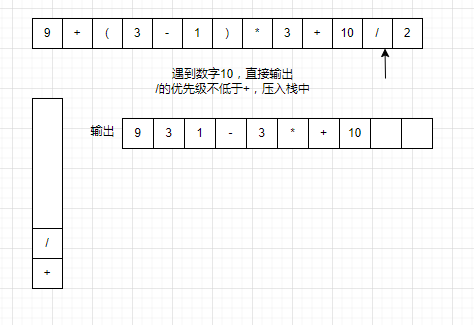
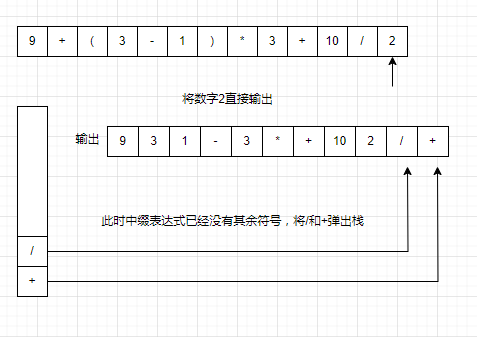
(1)判断压入栈中的符号的优先级是否高于栈顶,如果不高于栈顶,则将栈内的所有符号弹出,再把符号压入栈中
(2)将()括号内的符号弹出栈
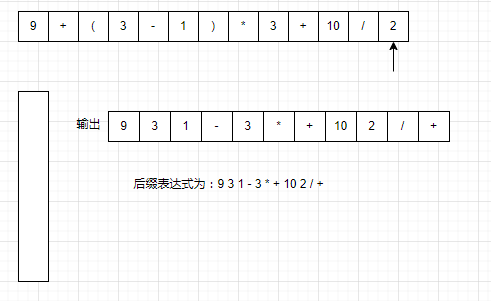
以9+(3-1)*3+10/2为例。



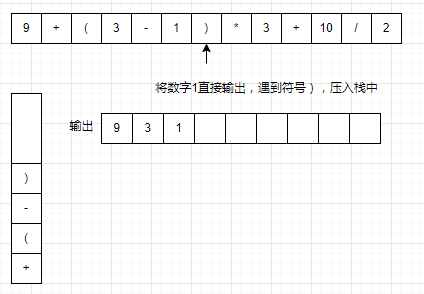
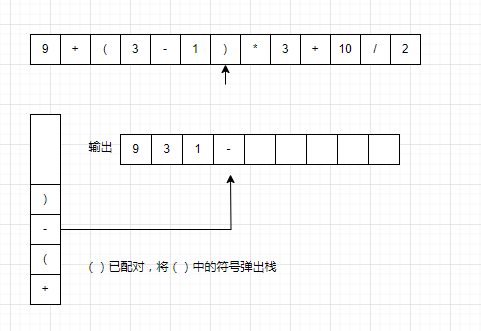

文末代码
typedef int datatype;
typedef struct stack
{
datatype* data;
int capacity;
int top;
}stack;
void StackInit(stack* ps);
void StackDestory(stack* ps);
void StackPush(stack* ps, datatype n);
void StackPop(stack* ps);
datatype StackTopData(stack* ps);
bool StackEmpty(stack* ps);
void StackInit(stack* ps)
{
if (ps == NULL)
{
ps = malloc(sizeof(stack));
return ;
}
ps->data = NULL;
ps->capacity = 0;
ps->top = 0;
}
void StackPush(stack* ps, datatype e)
{
assert(ps);
if (ps->capacity == ps->top)
{
int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
ps->capacity = newcapacity;
stack* tmp = realloc(ps->data, ps->capacity * sizeof(datatype));
assert(tmp);
ps->data = tmp;
}
ps->data[ps->top] = e;
ps->top++;
}
void StackPop(stack* ps)
{
if (StackEmpty(ps))
{
perror("Stack is empty\n");
return;
}
ps->top--;
}
bool StackEmpty(stack* ps)
{
return ps->top == 0;
}
datatype StackTopData(stack* ps)
{
if (StackEmpty(ps))
{
perror("Stack is empty\n");
exit(1);
}
return ps->data[ps->top - 1];
}
void StackDestory(stack* ps)
{
assert(ps);
free(ps->data);
ps->data = NULL;
ps->top = 0;
ps->capacity = 0;
}
int evalRPN(char** tokens, int tokensSize) {
stack* rpn=malloc(sizeof(stack));
StackInit(rpn);
int ret = 0;
while (tokensSize--)
{
if (**tokens == '+' ||
**tokens == '-' ||
**tokens == '*' ||
**tokens == '/')
{
if (strlen(*tokens) == 1)
{
int num1 = StackTopData(rpn);
StackPop(rpn);
int num2 = StackTopData(rpn);
StackPop(rpn);
switch (**tokens)
{
case '+':StackPush(rpn, num2 + num1);
break;
case'-':StackPush(rpn, num2 - num1);
break;
case'*':StackPush(rpn, num2 * num1);
break;
case'/':StackPush(rpn, num2 / num1);
break;
}
}
else {
int num = 0;
num = atoi(*tokens);
StackPush(rpn, num);
}
}
else
{
int num = 0;
num = atoi(*tokens);
StackPush(rpn, num);
}
tokens++;
}
ret = StackTopData(rpn);
StackDestory(rpn);
return ret;
}