ArrayDeque集合源码分析
文章目录
- ArrayDeque集合源码分析
- 一、字段分析
- 二、构造函数分析
- 方法、方法分析
- 四、总结
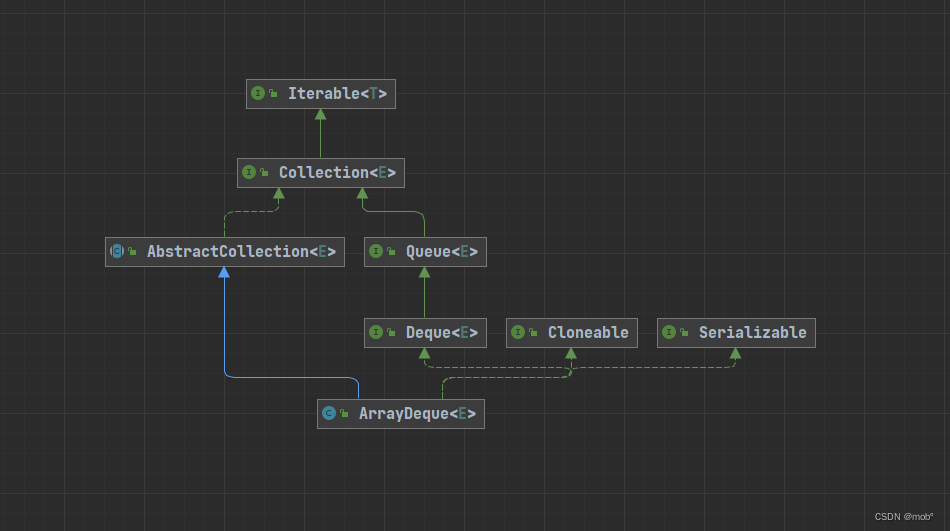
- 实现了 Deque,说面该数据结构一定是个双端队列,我们知道 LinkedList 也是双端队列,并且是用双向链表 存储结构的。而 ArrayDeque 则是使用 环形数组 来实现双端队列。各有优缺点。
- 实现代码比较少,难点在于使用了很多位运算进行了优化,来学习下ArrayDueue如何使用位运算代替 运算符的从而实现优化的。
一、字段分析
//用来存储元素的数组,这个数组可循环利用,有效数据范围为 [head, tail)注意tail 取不到
//也会出现tail < head 的情况,即前面的数据被废弃了,且tail到已经过了数组尾部了,然后跳到开始位置
//开始循环利用前面废弃的位置。
transient Object[] elements;
//指向头部有效数据
transient int head;
//指向尾部有效数据 + 1,或者理解为下一个添加元素的位置。整个过程,head 和 tail 都是不断变化的,head ~ tail - 1 范围内为有效数据。
//并不是tail 到达数组尾部即 elements.lengt - 1 就会扩容的。因为他可能复用前面可能发生废弃数组位置。
transient int tail;
//默认初始容量
private static final int MIN_INITIAL_CAPACITY = 8;
二、构造函数分析
//调用无参构造函数,直接创建一个容量为 16 的数组作为初始数组。
public ArrayDeque() {
elements = new Object[16];
}
//给定初始容量构建ArrayDeque,但并不是给 numElements 值为多少,就会创建多大的数组作为初始数组。
//给是判断并计算 最接近numElements的值,且为 2的幂次方的数作为初始容量。
public ArrayDeque(int numElements) {
//分配容量
allocateElements(numElements);
}
private void allocateElements(int numElements) {
//确定初始容量并构建数组,赋值给实际存储元素的 elements 数组
elements = new Object[calculateSize(numElements)];
}
//用来计算最终的容量的,计算结果为最接近 numElements 的数,且为 2的幂次方。
//比如 numElements = 15,则计算结果为 16(2^4)
//那么为什么一定要为 2的幂次方呢?为了在做取余运算时用位运算代替运算符运算,从而提高效率。
private static int calculateSize(int numElements) {
//拿到默认最小的初始值,值为8
int initialCapacity = MIN_INITIAL_CAPACITY;
// Find the best power of two to hold elements.
// Tests "<=" because arrays aren't kept full.
//传入的 参数 numElements 比默认最小值还小,则直接使用默认的最小值为初始容量。,否则进行
//计算,得到最接近 numElements ,且为 2 的次方的数。
if (numElements >= initialCapacity) {
initialCapacity = numElements;
//为什么这样的计算能够得到 最接近 numElements ,且为 2 的幂次方的数呢?
//首先列举下2的幂次方的二进制表示,来看下规律
//0001 : 2^0
//0010 : 2^1
//0100 : 2^3
//1000 : 2^4
//上面例子可以看出,如果想要是 2的幂次方,那么整个二进制表示只能有一个1,其他的
//1应该被消除,如果数中有不止一个1,那么最接近的应该是最高位的1前进一位,
//且其他未都是0,该数就是最接近,且为2的幂次方。
//消除1的方法有所有位 都为1 在 + 1,则得到结果就有一个1,
//如0111 + 1 =》 1000
//我们知道一个数的最高位那一定是1了,其他位可能有1或0,而这个算法就是将其位
//全部转化为1,之后再 + 1就是答案。
//我们知道 Integer一共是4个字节,即32 位。
//如果极限状态第31位是1(32位为1位负数,不会走当前逻辑,会给默认的最小初始容量)
//我们需要将31位右边所有位都转化为1,我换一种说话,将右边连续的三十一位都转化为1。
//将右边连续的2位转化为1
initialCapacity |= (initialCapacity >>> 1);
//将右边连续的4位转化为1
initialCapacity |= (initialCapacity >>> 2);
//将右边连续的8位转化为1
initialCapacity |= (initialCapacity >>> 4);
//将右边连续的16位转化为1
initialCapacity |= (initialCapacity >>> 8);
//将右边连续的32位转化为1,都能将连续的32位都转为1,你少于32的难道还不能转化为1吗。
initialCapacity |= (initialCapacity >>> 16);
//都转为1的基础上+1,就得到大于且最接近当前数,且为2的幂次方的数。
initialCapacity++;
//可能计算结果为负数,比如第31位为1,计算后变成最后一位(即符号位)变为1,成了负数
//所以Good luck allocating 2 ^ 30 elements 注释也给出了我们最大容量就是2^30
if (initialCapacity < 0) // Too many elements, must back off
initialCapacity >>>= 1;// Good luck allocating 2 ^ 30 elements
}
return initialCapacity;
}
public ArrayDeque(Collection<? extends E> c) {
//判断是否需要扩容
allocateElements(c.size());
//将集合c中所有元素添加到ArrayDeque中
addAll(c);
}
//将集合c中所有元素添加到ArrayDeque中
public boolean addAll(Collection<? extends E> c) {
boolean modified = false;
//循环遍历添加集合c中的元素
for (E e : c)
if (add(e))
modified = true;
return modified;
}
//添加元素e
public boolean add(E e) {
//添加元素到尾部
addLast(e);
return true;
}
//添加元素到尾部,即tail位置
public void addLast(E e) {
if (e == null)
throw new NullPointerException();
//呼应我前面介绍tail的,tail 为下一个添加元素的位置,所以直接在该位置添加。
elements[tail] = e;
//判断队列是否已满了,其实效果就是 tail + 1 后是否和 head 重合,即 tail + 1 == head ???
//如何理解这段代码呢,就要结合我上面说的 为什么 elements 的数组长度设计为 2的幂次方有关了!!
//正因为 elements.length 是2的幂次方,那么它 - 1 后二进制的最高位(该位置记为@)由 1 -> 0,而所有的低位变为1
//在和tail 做 & 运算时,就会将tail二进制 @ 位及更高位全部转化为0,而@后面的全部转化为1,
//相当于 tail % elements 做取余运算。
//所以将elements.length设为2的幂次方好处就是:在判断tail 与 head 的关系是,
//可用二进制运算取余代替 运算符取余运算,提高效率。
//name 有一个疑问了,为什么不直接用 tail + 1 == head ? 不就行了吗??算都不用算不是更快吗??
//因为要考虑越界的情况!!elements 是一个可循环使用的环形数组,比如 tail = elements.lenth - 1,tail + 1后越界了
//所以要做 & 运算!!
if ( (tail = (tail + 1) & (elements.length - 1)) == head)
//tail 与 head重合,需要扩容了
doubleCapacity();
}
private void doubleCapacity() {
//断言, head != tail 就会抛出异常。也可体现出,ArrayDequeue 当 head == tail 时,进行扩容。
assert head == tail;
//记录头结点
int p = head;
//当前数组容量
int n = elements.length;
//head 到 elements.length - 1 ,共有多少元素 (p,elements.length - 1]
int r = n - p; // number of elements to the right of p
//将数组的 容量扩容两倍
int newCapacity = n << 1;
//越界爬出异常
if (newCapacity < 0)
throw new IllegalStateException("Sorry, deque too big");
//使用扩容后的容量创建新的数组
Object[] a = new Object[newCapacity];
//相当于将 老数组 head 到 数组末尾的数据,复制到新数组中,复制到新数组下标0开始位置,长度就是r
//你可以理解为head位起始位置,从head一直复制到tail,依次复制给新数组,从0 开始的位置。
System.arraycopy(elements, p, a, 0, r);
//将老数组o 位置开始以此复制给新数组。
//这两部给个过程就明白了
//
// 1. element[0, 1, 2, 3, 4, 5] => newElements[3,4,5,0,0,0,0,0,0,0];
// head
// 2. element[0, 1, 2, 3, 4, 5] => newElements[3,4,5,0,1,2,0,0,0,0];
// head
System.arraycopy(elements, 0, a, r, p);
//elements 指向新的数组
elements = a;
//head 指向索引 0
head = 0;
//tail 指向最后一个位置的下一位,即下一个添加进ArrayDequeue元素的位置。
tail = n;
}
方法、方法分析
- 添加元素方法。
//添加元素到尾部,即tail位置
public void addLast(E e) {
if (e == null)
throw new NullPointerException();
//呼应我前面介绍tail的,tail 为下一个添加元素的位置,所以直接在该位置添加。
elements[tail] = e;
//判断队列是否已满了,其实效果就是 tail + 1 后是否和 head 重合,即 tail + 1 == head ???
//如何理解这段代码呢,就要结合我上面说的 为什么 elements 的数组长度设计为 2的幂次方有关了!!
//正因为 elements.length 是2的幂次方,那么它 - 1 后二进制的最高位(该位置记为@)由 1 -> 0,而所有的低位变为1
//在和tail 做 & 运算时,就会将tail二进制 @ 位及更高位全部转化为0,而@后面的全部转化为1,
//相当于 tail % elements 做取余运算。
//所以将elements.length设为2的幂次方一个好处就是:在判断tail 与 head 的关系是,
//可用二进制运算取余代替 运算符取余运算,提高效率。
//name 有一个疑问了,为什么不直接用 tail + 1 == head ? 不就行了吗??算都不用算不是更快吗??
//因为要考虑越界的情况!!elements 是一个可循环使用的环形数组,比如 tail = elements.lenth - 1,tail + 1后越界了
//所以要做 & 运算!!
if ( (tail = (tail + 1) & (elements.length - 1)) == head)
//tail 与 head重合,需要扩容了
doubleCapacity();
}
//向 head - 1 处添加元素
public void addFirst(E e) {
if (e == null)
throw new NullPointerException();
//取余运算,同时防止了越界。将head - 1 处复制e
elements[head = (head - 1) & (elements.length - 1)] = e;
//判断是否扩容
if (head == tail)
//扩容,扩容方法看构造方法里介绍了
doubleCapacity();
}
//向 tail 位置添加元素
public void addLast(E e) {
if (e == null)
throw new NullPointerException();
//直接给tail 位置赋值
elements[tail] = e;
//取余元素,判断是否扩容
if ( (tail = (tail + 1) & (elements.length - 1)) == head)
//扩容
doubleCapacity();
}
//向 tail 处添加元素
public boolean offerLast(E e) {
addLast(e);
return true;
}
//向 head - 1 处添加元素
public boolean offerFirst(E e) {
addFirst(e);
return true;
}
//向tail 处添加元素
public boolean add(E e) {
addLast(e);
return true;
}
//向tail 处添加元素
public boolean offer(E e) {
return offerLast(e);
}
//向 head - 1处添加元素
public void push(E e) {
addFirst(e);
}
- 获取元素方法。
//弹出 head 位置元素
public E pollFirst() {
int h = head;
@SuppressWarnings("unchecked")
E result = (E) elements[h];
// Element is null if deque empty
if (result == null)
return null;
//弹出后将head位置设为null
elements[h] = null; // Must null out slot
//获取head的下一个位置,取余运算防止越界。
head = (h + 1) & (elements.length - 1);
//返回结果
return result;
}
//弹出 tail - 1 处元素
public E pollLast() {
//获取元素位置,取余防止越界
int t = (tail - 1) & (elements.length - 1);
@SuppressWarnings("unchecked")
E result = (E) elements[t];
if (result == null)
return null;
//弹出后,该位置设为null
elements[t] = null;
//新的tail
tail = t;
return result;
}
//获取head位置元素,但不弹出
public E getFirst() {
@SuppressWarnings("unchecked")
E result = (E) elements[head];
if (result == null)
throw new NoSuchElementException();
return result;
}
//获取tail-1位置处元素,但不弹出
public E getLast() {
@SuppressWarnings("unchecked")
E result = (E) elements[(tail - 1) & (elements.length - 1)];
if (result == null)
throw new NoSuchElementException();
return result;
}
//获取head位置元素,但不弹出
public E peekFirst() {
// elements[head] is null if deque empty
return (E) elements[head];
}
//获取tail-1位置处元素,但不弹出
public E peekLast() {
return (E) elements[(tail - 1) & (elements.length - 1)];
}
//弹出 head 位置元素
public E poll() {
return pollFirst();
}
//获取head位置元素,但不弹出
public E element() {
return getFirst();
}
//获取head位置元素,但不弹出
public E peek() {
return peekFirst();
}
//弹出 head 位置元素
public E pop() {
return removeFirst();
}
- 移除元素方法:
//删除 head 处元素
public E removeFirst() {
//删除 head 处元素
E x = pollFirst();
if (x == null)
throw new NoSuchElementException();
//返回被删除的元素
return x;
}
//删除 tail - 1 处的元素
public E removeLast() {
删除 tail - 1 处的元素
E x = pollLast();
if (x == null)
throw new NoSuchElementException();
//返回被删除的元素
return x;
}
//删除 head 处元素
public E pollFirst() {
//记录head位置
int h = head;
@SuppressWarnings("unchecked")
//记录head处元素,用于返回
E result = (E) elements[h];
// Element is null if deque empty
if (result == null)
return null;
//将head处元素设为空
elements[h] = null; // Must null out slot
//计算新的head,取余元素防止越界
head = (h + 1) & (elements.length - 1);
return result;
}
//删除 tail - 1 处的元素
public E pollLast() {
//获取 tail -1 位置下标,取余运算,防止越界
int t = (tail - 1) & (elements.length - 1);
@SuppressWarnings("unchecked")
//获取删除元素位置
E result = (E) elements[t];
if (result == null)
return null;
//tail - 1位置被置空
elements[t] = null;
//更新tail位置
tail = t;
return result;
}
//删除head处元素
public E remove() {
return removeFirst();
}
//删除head出元素
public E poll() {
return pollFirst();
}
//删除head处元素
public E pop() {
return removeFirst();
}
-
扩容方法:在介绍构造函数时,一并介绍了。
-
迭代器:
private class DeqIterator implements Iterator<E> {
/**
* Index of element to be returned by subsequent call to next.
*/
//用于记录迭代得到下一个元素的下标位置。初始值当时是head了。
private int cursor = head;
/**
* Tail recorded at construction (also in remove), to stop
* iterator and also to check for comodification.
*/
//用于记录迭代的中止位置
private int fence = tail;
/**
* Index of element returned by most recent call to next.
* Reset to -1 if element is deleted by a call to remove.
*/
//用于记录最后一次迭代得到的元素位置,迭代还未开始,当然给-1了。
private int lastRet = -1;
//判断是否还有元素可以迭代
public boolean hasNext() {
return cursor != fence;
}
//迭代获取下一个元素
public E next() {
//无元素了,报错
if (cursor == fence)
throw new NoSuchElementException();
@SuppressWarnings("unchecked")
//获取cursor处的位置元素
E result = (E) elements[cursor];
// This check doesn't catch all possible comodifications,
// but does catch the ones that corrupt traversal
//判断迭代过程中集合是否被修改过。和 modCount作用相同
if (tail != fence || result == null)
throw new ConcurrentModificationException();
//记录最后一次迭代得到元素的位置
lastRet = cursor;
//获取下一次迭代元素位置下标,位运算,防止越界
cursor = (cursor + 1) & (elements.length - 1);
return result;
}
//迭代删除,删除的是最后以此迭代得到的元素
public void remove() {
//以此还被迭代呢,删除失败
if (lastRet < 0)
throw new IllegalStateException();
//删除元素
if (delete(lastRet)) { // if left-shifted, undo increment in next()
cursor = (cursor - 1) & (elements.length - 1);
fence = tail;
}
//上一次迭代的元素被删除了,所以即为-1。所以迭代过程中不能连续remove。
lastRet = -1;
}
}
四、总结
- 使用的是可循环使用的双指针数组来存储结构。可以有效的减少扩容次数,并且提高资源利用率。不支持存储null元素。
- 是线程不安全的。
- 可当做链表,栈,队列使用。在头部和尾部插入或者删除元素,时间复杂度为 O(1),但是在扩容的时候需要批量移动元素,其时间复杂度为 O(n)。
- 扩容的时候,将数组长度扩容为原来的 2 倍,即 n << 1。