广度优先搜索
广度优先搜索(Breadth-First-Search,BFS)类似于二叉树的层序遍历算法(借助队列),其基本思想是:首先访问起始顶点,接着由v出发,依次访问v的各个未访问过的邻接顶点w1,W2,…,Wn,然后依次访问w1,W2,…,Wn的所有未被访问过的邻接顶点;再从这些访问过的顶点出发,访问它们所有未被访问过的邻接顶点……以此类推,直到图中所有顶点都被访问过为止。Dijkstra 单源最短路径算法和Prim最小生成树算法也应用了类似的思想。
广度优先搜索是一种分层的查找过程,每向前走一步可能访问一批顶点,不像深度优先拽索那样有往回退的情况,因此它不是一个递归的算法。为了实现逐层的访问,算法必须借助一个辅助队列,以记忆正在访问的顶点的下一层顶点。
广度优先拽索算法的伪代码如下:
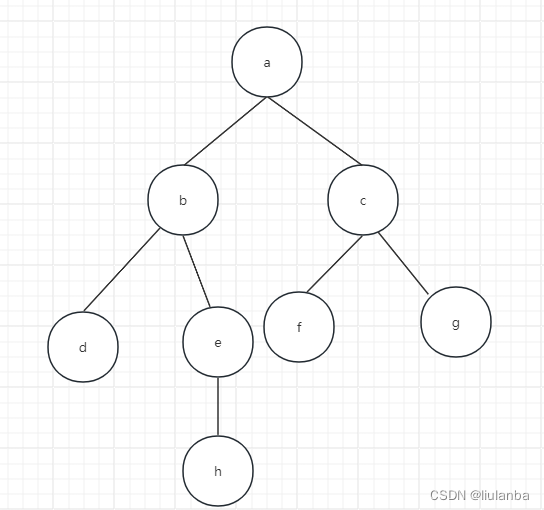
下面通过实例演示广度优先搜索的过程,给定图G如下。假设从a结点开始访问,a先入队。此时队列非空,取出队头元素a.由于b、c与a邻接且未被访问过,于是依次访问b、c,并将b、c依次入队。队列非空,取出队头元素b,依次访问与b邻接且未被访问的顶点d、e,并将d、e入队(注意:a与b也邻接,但a己置访问标记,故不再重复访问)。此时队列非空,取出队头元素c,访间与c邻接且未被访问的顶点f、g,并将f、g入队。此时,取出队头元素d,但与d邻接且未被访问的顶点一个无向图G为空,故不进行任何操作。继续取出队头元素e,将h入队列……最终取出队列头元素h后,队列为空,从而抵环自动跳出。遍历结果为 abcdefh
从上例不难看出,图的广度优先搜索的过程与二叉树的层序遍历是完全一致的,这也说明了图的广度优先搜索遍历算法是二叉树的层次遍历算法的扩展。
1.BFS算法的性能分析
无论是邻接表还是邻接矩阵的存储方式,BFS算法都需要借助一个辅助队列Q,n个顶点均需入队一次,在最坏的情况下,空间复杂度为0(V)。
采用邻接表存储方式时,每个顶点均需搜索一次(或入队一次),故时间复杂度为0(V),在搜索任一顶点的邻接点时,每条边至少访问一次,故时间复杂度为 0(E),算法总的时间复杂度为0(V+E)。采用邻接矩阵存储方式时,查找每个顶点的邻接点所需的时间为O(V),故算法总的时间复杂度为0(V²)。
2.BFS算法求解单源最短路径问题
若图G=(V,E)为非带权图,定义从顶点u到顶点v的最短路径d(u,v)为从u到v的任何路径中最少的边数;若从u到v没有通路,则d(u,v)=∞。
使用BFS,我们可以求解一个满足上述定义的非带权图的单源最短路径问题,这是由广度优先搜索总是按照距离由近到远来遍历图中每个顶点的性质决定的。
BFS 算法求解单源最短路径问题的算法如下:
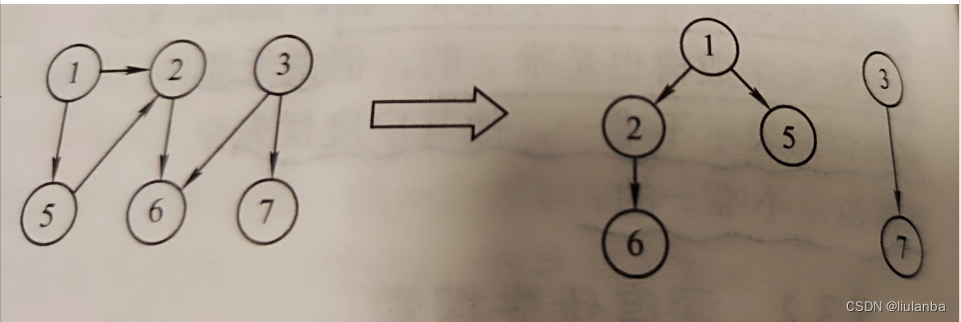
3.广度优先生成树
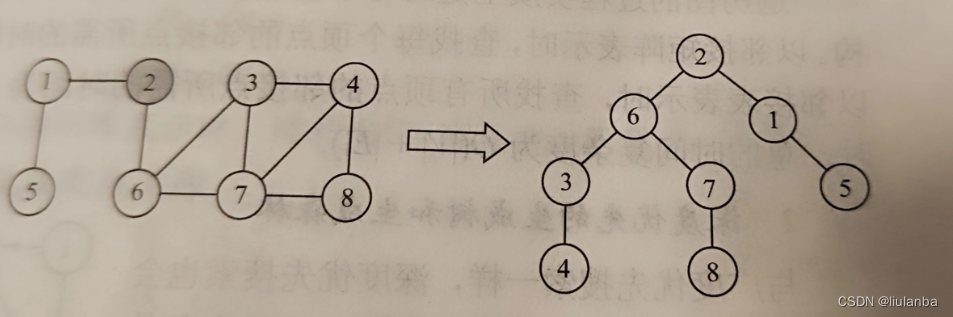
在广度遍历的过程中,我们可以得:请需得到一棵遍历树,称为广度优先生成树,0
如图5.12所示。需要注意的是,一给定图的邻接矩阵存储表示是唯一的,故其广度优先生成树也是唯一的,但由于邻接表存储表示不唯一,故其广度优先生成树也是不唯一的。
深度优先搜索
与广度优先搜索不同,深度优先搜索(Depth-First-Search,DFS)类似于树的先序遍历)如其名称中所暗含的意思一样,这种搜索算法所遵循的搜索策略是尽可能“深”地拽索一个图。
它的基本思想如下:首先访问图中某一起始顶点v,然后由v出发,访问与v邻接且未被访问的任顶点1,再访问与m1邻接且未被访问的任一顶点w2…重复上述过程。当不能再继续向下访间时,依次退回到最近被访问的顶点,若它还有邻接顶点未被访问过,则从该点开始继续上述拟索过程,直到图中所有顶点均被访问过为止。
其递归形式的算法十分简洁,算法过程如下:
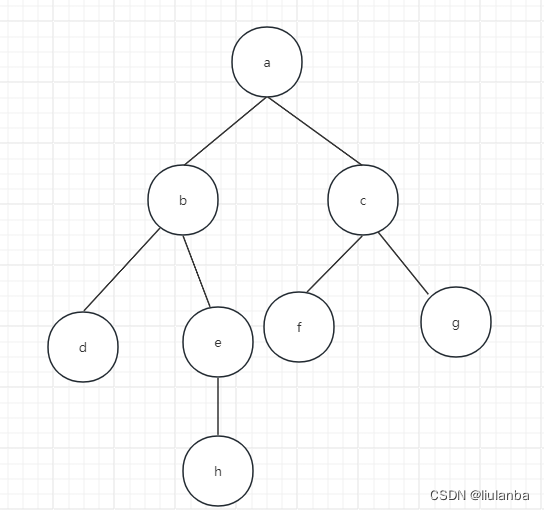
以图所示的无向图为例,演示深度优先搜索的过程:首先访问a,并置a己访问标记。然后访问与a邻接且未被访问的顶点b,置b已访问标记;然后访问与b邻接且未被访问的顶点d,置d已访问标记。此时d已没有未被访问过的邻接点,故返回上一个访问过的顶点b,访问与其邻接且未被访问的顶点e,置e访问标记……以此类推,直到图中所有的顶点访问一次且仅访问一次。遍历结果为abdehcfg
注意:图的邻接矩阵表示是唯一的,但对于邻接表来说,若边的输入次序不同,生成的邻接表也不同。因此,对于同样一个图,基于邻接矩阵的遍历所得到的 DFS 序列和 BFS序列是唯一的,基于邻接表的遍历所得到的DFS 序列和BFS序列是不唯一的。
1.DFS算法的性能分析
DFS 算法是一个递归算法,需要借助一个递归工作栈,故其空间复杂度为0(V)。
遍历图的过程实质工是对每个顶点查我其邻接点的过程,其耗费的时间取决于所用的存储结构。以邻接矩阵表示时,查找每个顶点的邻接点所需的时间为0(V),故总的时间复杂度为0(V²).以邻接表表示时,查找所有顶点的邻接点所需的时间为O(E),访问顶点所需的时间为0(V)),此时,总的时间复杂度为O(V+|E|)
2.深度优先的生成树和生成森林
与广度优先拽索一样,深度优先拽索也会产生一棵深度优先生成树。当然,这是有条件的,即对连通图调用DFS才能产生深度优先生成树,否则产生的将是深度优先生成森林,如图5.13所示。与BFS类似,基于邻接表存储的深度优先生成树是不唯一的。