数论＜1＞——数论基础

news2025/6/20 12:59:43

这期博客是一个数论入门介绍，dalao们可以自动忽略。

Part 1:素数(质数)

说到数论，小学奥数里也有。我最先想到的就是质数了。素数就是一个只能被1和它自己整除的数。判断的方法也很简单，可以 $\Theta (n)$ 扫一遍就结束了，但是没必要。由于一个数的因数肯定分布在 $\Theta (\sqrt{n})$ 的左边和右边。因此，只用扫描到 $\sqrt{n}$ 就够了。

bool isprime(int n){
	if(n<2)//0和1都不是质数 
		return false;
	for(int i=2;i<=n/i;i++){//这里i<=n/i是一个防止i*i爆int以及sqrt(n)精度不好的小技巧 
		if(n%i==0)
			return false;
	}
	return true;
}

现在，我们知道如何判断一个数是不是质数的方法了。现在，我们向分解G(质因)数。我们 $\Theta (\sqrt n)$ 的扫描，只要i是n的因数，就把i塞进一个map里，然后除掉n里面所有的i。这样就保证了每个i都是素数，顺便记录次数。最后，有可能n不为0，所以要特判。

map<int,int> fac;//分别是:质因子,次数
for(int i=2;i<=n/i;i++){
	if(n%i==0){
		while(n%i==0){
			n/=i;
			fac[i]++;
		}
	}
}
if(n)//特判
	fac[n]=1;

在这里，我补充几个公式:

唯一分解定理: $N=p_{1}^{\alpha _{1}} \cdot p_{2}^{\alpha _{2}} \cdot ......\cdot p_{k}^{\alpha_{k}}$

因数个数定理: $(\alpha_{1}+1)\cdot (\alpha_{2}+1) \cdot ......(\alpha_{k}+1)$

因数和定理: $(p_{1}^{0}+p_{1}^{1}+...+p_{1}^{\alpha_{1}})\cdot (p_{2}^{0}+p_{2}^{1}+...+p_{2}^{\alpha_{2}})\cdot ......\cdot (p_{k}^{0}+p_{k}^{1}+...+p_{k}^{\alpha_{k}})$

-------------------------------------------------华丽的分割线--------------------------------------------------------

接下来，我们来谈一个比较有意思的东西。首先，如果我让你打印100以内的素数表，你会怎么做？根据刚刚的判断素数的方法，我们可以 $\Theta (n \sqrt{n})$ 的解决这个问题。但是如果数据放大到 $10^6$ 甚至 $10^7$ ，怎么办？

这就要用到素数筛了。素数筛就是一种算法，可以帮你快速筛出素数。有两种筛法，埃筛和欧筛。分别由欧拉和bla~bla~(埃拉托色尼)发明的。先说埃氏筛法(因为好懂)，这个算法的核心就是素数的倍数一定是合数。然后，我们就可以愉快的写代码了。

bool isprime[maxn];
void sieve(){
	memset(isprime,true,sizeof(isprime));
  	isprime[0]=isprime[1]=false;
  	for (int i=2;i<=maxn/i;i++){
    	if(isprime[i]){
      		for(int j=i*i;j<=maxn;j+=i)
	  			isprime[j]=false;
	  	}
  	}
}

埃筛的复杂度为 $\Theta (n \: log \: log \: n)$ ，略微有点高，但是好记。

接下来我们来看看复杂度接近 $\Theta (n)$ 的欧拉筛。埃筛的问题在于素数会被标记多次，那我们优化的方法就是让合数只被标记一次。同时，欧拉筛也叫线性筛(复杂度是线性的嘛)。

bool notprime[maxn];
vector<int> prime;
void sieve(){
	notprime[1]=true;
  	for(int i=2;i<=maxn;i++){
    	if(!notprime[i])
      		prime.push_back(i);
    	for(int x:prime){
      		if(i*x>maxn)
			  	break;
      		notprime[i*x]=true;
      		if(i%x==0)
        		break;
    	}
  	}
}

注意，一定要用notprime，不然又回到埃筛了。

这里就不放例题了，因为其实就是板子。

Part 2:最大公因数和最小公倍数

最大公因数和最小公倍数都是小学奥数学过的东西。但还是稍微介绍一下吧。顾名思义，最大公约数是两个数最大的公约数，最小公倍数是两个数最小的公倍数。接下来，我们来看看如何求最大公约数和最小公倍数。

最大公约数:辗转相除法，即 $gcd(a,b)=gcd(b,a \: mod \: b) \: (a<b)$ 。证明嘛，我不大会，但......

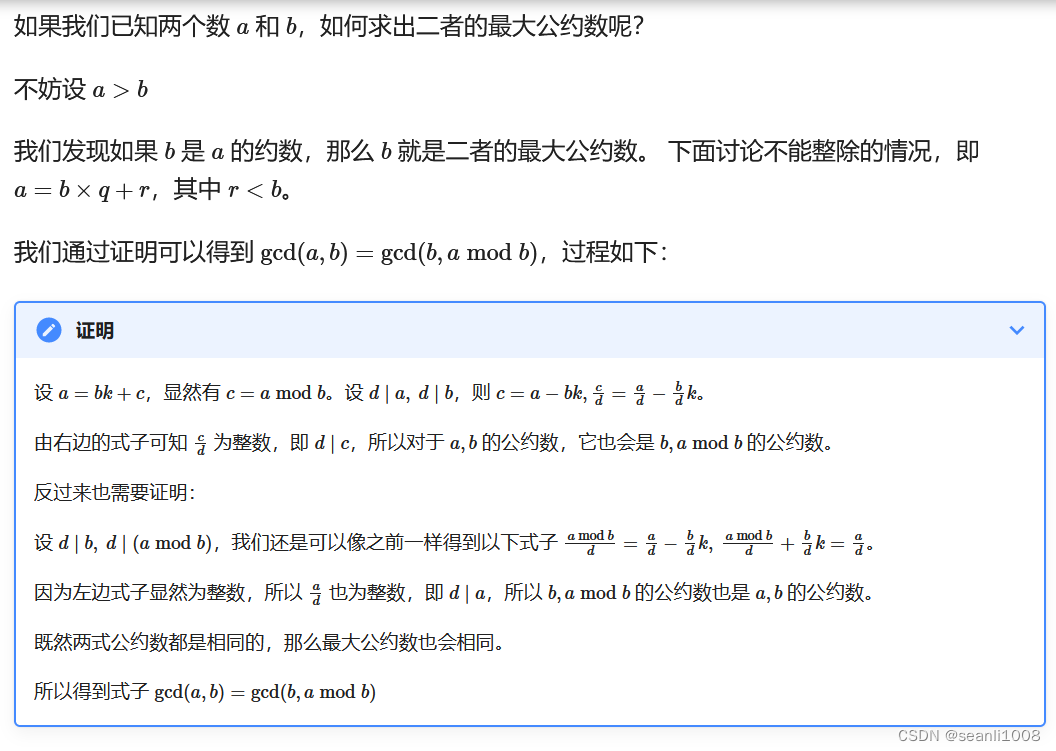
OI-Wiki！

放个代码。

int gcd(int a,int b){
    if(b==0)
        return a;
    return gcd(a,b%a);
}
//当然,STL里有一个函数叫__gcd
//它也可以求gcd,所以我们就不用自己写啦(*^▽^*)

顺便说一句，如果gcd(a,b)=1，那我们称a,b互质。欧几里得算法时间复杂度 $\Theta (log \: max(a,b))$ 。

接下来看最小公倍数的求法。先给结论:

int lcm(int a,int b){
    return a*b/__gcd(a,b);
}

为什么？我们令 $a=p_1^{k_{a_{1}}}\cdot p_2^{k_{a_{2}}}\cdot ...\cdot p_s^{k_{a_{s}}}$ , $b=p_1^{k_{b_{1}}}\cdot p_2^{k_{b_{2}}}\cdot ...\cdot p_s^{k_{b_{s}}}$ ，那么:

$(a,b)=p_1^{min(k_{a_{1}},k_{b_{1}})}\cdot p_2^{min(k_{a_{2}},k_{b_{2}})}\cdot ...\cdot p_s^{min(k_{a_{s}},k_{b_{s}})}$

$[a,b]=p_1^{max(k_{a_{1}},k_{b_{1}})}\cdot p_2^{max(k_{a_{2}},k_{b_{2}})}\cdot ...\cdot p_s^{max(k_{a_{s}},k_{b_{s}})}$

由于 $k_a+k_b=max(k_a,k_b)+min(k_a+k_b)$ ，所以 $a\times b=lcm(a,b)\times gcd(a,b)$ 。

Part 3:扩展欧几里得

我们先来看一个方程: $ax+by=c$ 而它，是终极大Boss。那么它什么时候有解呢？

当 $(a,b)\mid c$ 是，方程有解。So，c必然是 $gcd(a,b)$ 的倍数。所以，我们先看 $ax+by=(a,b)$ 的情况，这也是扩展欧几里得解决的问题。

根据欧几里得算法，得 $ax+by=gcd(a,b)=gcd(a,a \: mod \: b)$ ，接下来递归又变成了这个↓

$bx+(a \: mod \: b)y=gcd(b, a \: mod \: b)$ 。我们叫这个 $bx_1+(a \: mod \: b)y_1=gcd(b,a \: mod \: b)$

然后就知道 $ax_0+by_0=bx_1+(a \: mod \: b)y_1$ ，所以 $x_0=y_1,y_0=x_1-(a*b)/y_1$ 。

当你递归到最后一层，也就是b=0的时候，你就解得 $x'=1,y' \epsilon R$ 。然后我们在向上递归，得出开

始的x和y。Talk is cheap,show me your code.

int exgcd(int a,int b,int &x,int &y){
	if(b==0){
		x=1;
		y=0;
		return a;
	}
	int res=exgcd(b,a%b,x,y);
	int tmp=x;
	x=y;
	y=tmp-a/b*y;
	return res;
}

说了这么多，来练练手吧。

P1082:

乍一看，你可能会问:这和扩展欧几里得有啥关系？问的有理，我们来做一些恒等变形。

$ax\equiv 1(mod\:b)$ 其实相当于 $ax+by=1$ 。可这还是跟 $ax+by=(a,b)$ 不一样啊，没关系。有

解的情况是 $c\mid gcd(a,b)$ ，而1一定满足。现在，它就变成了exgcd的板子题啦！

#include <bits/stdc++.h>
using namespace std;
//exgcd
int main(){
	int a,b,x,y;
	cin>>a>>b;
	int res=exgcd(a,b,x,y);
	if(x<0)
		x+=b;
	cout<<x<<endl;
	return 0;
}

ABC186E:

洛谷上也有。转圈，不难想到同余。

我们可以列出方程 $S+Kx\equiv 0\: (mod\: N)$ ，得 $Kx\equiv -S\: (mod \: N)$ ，再把右边加上N，解x就

ok了。和上一题相似。

#include <bits/stdc++.h>
using namespace std;
long long x,y;
long long exgcd(long long a,long long b){
	if(b==0){
		x=1;
		y=0;
		return a;
	}
	long long res=exgcd(b,a%b);
	long long tmp=x;
	x=y;
	y=tmp-a/b*y;
	return res;
}
long long main(){
	int T;
	cin>>T;
	while(T--){
		long long N,S,K;
		cin>>N>>S>>K;
		long long res=exgcd(K,N);
		long long t=(N-S)%N;
		if(t%res)
			cout<<-1<<endl;
		else
			cout<<(x%N+N)%N*(t/res)%(N/res)<<endl;	
	}
	return 0;
}

P1516:

这两个青蛙是真够笨的。

起点是a,b;速度是m,n;步数是t;套圈k次，得 $(m-n)t-lq=b-a$ 。一个不定方程！所以用扩展

欧几里得算法求解。

//十年OI一场空,不开long long见祖宗
#include <bits/stdc++.h>
using namespace std;
int exgcd(int a,int b,int &x,int &y){
	if(b==0){
		x=1;
		y=0;
		return a;
	}
	int res=exgcd(b,a%b,x,y);
	int tmp=x;
	x=y;
	y=tmp-a/b*y;
	return res;
}
int main(){
	int a,b,m,n,l,t,q;
	cin>>a>>b>>m>>n>>l;
	if(m<n){
		swap(m,n);
		swap(a,b);
	}
	int res=exgcd(m-n,l,t,q);
	if((b-a)%res!=0){
		cout<<"Impossible"<<endl;
		return 0;
	}
	int ans=t*(b-a)/res;
	int step=l/res;
	ans%=step;
	if(ans<0)
		ans+=step;
	cout<<ans<<endl;
	return 0;
}

好了Y(^o^)Y，以上就是本期的全部内容了。我们下期再见！

友情提醒:本期的题解代码都有问题，请不要无脑Ctrl C+Ctrl V

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1503396.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！