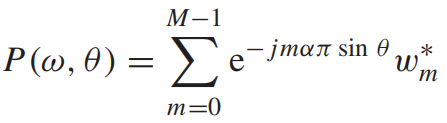已知一个系统的传递函数，如何进行硬件化呢？
只需要将传递函数离散化，得到差分方程，就可以根据差分方程进行硬件设计。

通过例子说明：

得到差分方程后，其中y(k)/y(k-1)/y(k-2)/u(k-1)/u(k-2)等代表不同周期系统输入输出数据，根据公式，进行硬件设计计算，即可得到系统输出。

常用的离散化方法有：

前向差分法；
后向差分法：
双线性变换法；
零阶保持器法；
一阶保持器法；
脉冲响应不变法；
前三种方法比较简单，传递函数中，直接用 z和s的关系进行替换就行：

其中Ts为离散化采样时间。

也可以通过matlab进行转化,下例采用零阶保持法（zoh）:
%%-------传递函数离散化------
num=[39610^(-9),12*10(-6)];
den=[3310^(-10),10(-13),0];
sys=tf(num,den);
step(sys);
%bode(sys);

ts=0.000001; %1M采样率，对应硬件设计模块运行频率

dsys=c2d(sys,ts,‘zoh’); %zoh method
[num1,den1]=tfdata(dsys,‘v’);
%dbode(num1,den1,ts,‘r’);
%%-------离散化分子分母转换为C语言程序使用------
%%-------+Y/U=0.00012z-0.00012/z^2-2z+1–
%%-------分子分母除以z ^ 2=>0.00012z ^ (-1)-0.00012z ^ (-2)/1-2z ^ (-1)+z^(-2)–
%%-------y(k)=2y(k-1)-y(k-2)+0.00012u(k-1)-0.00012*u(k-2);
u_1=0.0;u_2=0.0;
y_1=0.0;y_2=0.0;

%%-----阶跃响应验证

for k=1:1:2000
time(k) = k*ts;
yd(k) = 1;
u(k) = 1;

y(k)=-den1(2)*y_1-den1(3)*y_2+num1(2)*u_1+num1(3)*u_2;
u_2=u_1;u_1=u(k);
y_2=y_1;y_1=y(k);

end
figure(2);
%bode(dsys);
plot(time,yd,‘r’,time,y,‘k:’,‘linewidth’,2);
xlabel(‘times(2)’);ylabel(‘yd,y’);
legend(‘yd’,‘y’);