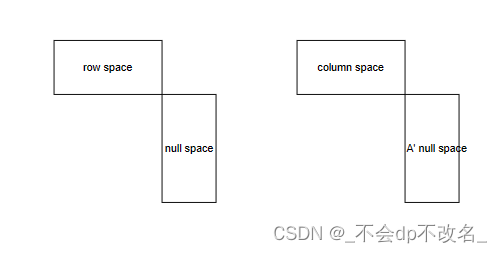
0. 四个子空间
1. 正交向量
两向量点乘为0,向量正交。
A
⊤
B
=
0
A^{\top}B=0
A⊤B=0
勾股定理
∣
∣
x
∣
∣
2
+
∣
∣
y
2
∣
∣
=
∣
∣
x
+
y
∣
∣
2
||x||^2+||y^2||=||x+y||^2
∣∣x∣∣2+∣∣y2∣∣=∣∣x+y∣∣2
验证正交条件
∣ ∣ x ∣ ∣ 2 = x ⊤ x = x x ⊤ ∣ ∣ y ∣ ∣ 2 = y ⊤ y = y y ⊤ ∣ ∣ x ∣ ∣ 2 + ∣ ∣ y 2 ∣ ∣ = ∣ ∣ x + y ∣ ∣ 2 ⟺ x ⊤ x + y ⊤ y = ( x + y ) ( x + y ) ⊤ = ( x + y ) ( x ⊤ + y ⊤ ) = x x ⊤ + x y ⊤ + y x ⊤ + y y ⊤ y x ⊤ = x ⊤ y = x y ⊤ = x ⊤ y 2 x ⊤ y = 0 x ⊤ y = 0 ||x||^2=x^{\top}x=xx^{\top}\\ ||y||^2=y^{\top}y=yy^{\top}\\ ||x||^2+||y^2||=||x+y||^2 \iff\\ x^{\top}x+y^{\top}y=(x+y)(x+y)^{\top}=(x+y)(x^{\top}+y^{\top})=\\ xx^{\top}+xy^{\top}+yx^{\top}+yy^{\top}\\ yx^{\top}=x^{\top}y=xy^{\top}=x^{\top}y\\ 2x^{\top}y=0\\ x^{\top}y=0 ∣∣x∣∣2=x⊤x=xx⊤∣∣y∣∣2=y⊤y=yy⊤∣∣x∣∣2+∣∣y2∣∣=∣∣x+y∣∣2⟺x⊤x+y⊤y=(x+y)(x+y)⊤=(x+y)(x⊤+y⊤)=xx⊤+xy⊤+yx⊤+yy⊤yx⊤=x⊤y=xy⊤=x⊤y2x⊤y=0x⊤y=0
也即垂直的条件
x
⊤
y
=
0
x^{\top}y=0
x⊤y=0
举例:
x
=
[
1
2
3
]
y
=
[
2
−
1
0
]
x
+
y
=
[
3
1
3
]
∣
x
∣
2
+
∣
y
∣
2
=
1
+
4
+
9
+
4
+
1
=
19
∣
x
+
y
∣
2
=
9
+
9
+
1
=
19
x=\begin{bmatrix} 1 \\ 2\\ 3 \end{bmatrix} y=\begin{bmatrix}2 \\ -1\\ 0 \end{bmatrix}\\ x+y=\begin{bmatrix} 3 \\ 1\\ 3 \end{bmatrix}\\ |x|^2+|y|^{2}=1+4+9+4+1=19\\ |x+y|^2=9+9+1=19
x=
123
y=
2−10
x+y=
313
∣x∣2+∣y∣2=1+4+9+4+1=19∣x+y∣2=9+9+1=19
2. 正交子空间
空间
S
S
S正交空间
T
T
T:
∀
s
→
∈
S
,
∀
t
→
∈
T
:
s
→
t
→
=
0
⟺
s
→
⊥
t
→
\forall \overrightarrow{s} \in S,\forall \overrightarrow{t} \in T: \overrightarrow{s}\overrightarrow{t}=0 \iff \overrightarrow{s} \perp \overrightarrow{t}
∀s∈S,∀t∈T:st=0⟺s⊥t
方阵行空间 C ( A ⊤ ) C(A^{\top}) C(A⊤)与零空间 N ( A ) N(A) N(A)正交证明
A
X
=
0
[
r
1
r
2
r
3
.
.
.
r
m
]
y
=
[
r
1
r
2
r
3
.
.
.
r
m
]
[
x
1
x
2
r
3
.
.
.
r
n
]
=
[
0
0
0
.
.
.
0
]
AX=0\\ \begin{bmatrix} r_1\\r_2\\r_3\\...\\r_m \end{bmatrix} y=\begin{bmatrix} r_1\\r_2\\r_3\\...\\r_m \end{bmatrix} \begin{bmatrix} x_1\\x_2\\r_3\\...\\r_n \end{bmatrix}= \begin{bmatrix} 0\\0\\0\\...\\0 \end{bmatrix}
AX=0
r1r2r3...rm
y=
r1r2r3...rm
x1x2r3...rn
=
000...0
可以得到
y
⊥
r
k
y
⊥
a
k
r
k
y
⊥
∑
k
=
1
m
a
k
r
k
y \perp r_k\\ y \perp a_kr_k\\ y \perp \sum_{k=1}^{m}a_kr_k
y⊥rky⊥akrky⊥k=1∑makrk
y
y
y为
N
(
A
)
N(A)
N(A)空间任意一向量,所以得证。
N ( A ) 与 C ( A ⊤ ) N(A)与C(A^{\top}) N(A)与C(A⊤)是空间 R n R^{n} Rn中的正交全集。
3. 求解无解的 A X = b AX=b AX=b
求解无解的
A
X
=
b
AX=b
AX=b是什么意思呢?
假设矩阵
m
>
n
m \gt n
m>n,
b
b
b不能由
A
A
A中各列线性组合得到时。
实际情况就是,测量数据多于实际需要数据;
测量数据中可能混入了出错的数据,我们需要把错误的数据给筛选出去。
解决办法: 同时左乘
A
⊤
A^{\top}
A⊤变为了一个对称矩阵。
A
X
=
b
⟶
A
⊤
A
X
^
=
A
⊤
b
AX=b \longrightarrow A^{\top}A\hat{X}=A^{\top}b
AX=b⟶A⊤AX^=A⊤b
N
(
A
⊤
A
)
N(A^{\top}A)
N(A⊤A)
不一定总可逆。
若矩阵
A
=
[
1
1
1
2
1
5
]
A
⊤
=
[
1
1
1
1
2
5
]
A
⊤
A
=
[
3
8
8
30
]
A= \begin{bmatrix} 1 & 1\\ 1 & 2\\ 1 & 5\\ \end{bmatrix} A^{\top}= \begin{bmatrix} 1 & 1 & 1\\ 1 & 2 & 5\\ \end{bmatrix}\\ A^{\top}A= \begin{bmatrix} 3 & 8\\ 8 & 30\\ \end{bmatrix}
A=
111125
A⊤=[111215]A⊤A=[38830]
此时
A
⊤
A
A^{\top}A
A⊤A可逆
若
A
=
[
1
1
1
1
1
1
]
A
⊤
=
[
1
1
1
1
1
1
]
A
⊤
A
=
[
3
3
3
3
]
A= \begin{bmatrix} 1 & 1\\ 1 & 1\\ 1 & 1\\ \end{bmatrix} A^{\top}= \begin{bmatrix} 1 & 1 & 1\\ 1 & 1 & 1\\ \end{bmatrix}\\ A^{\top}A= \begin{bmatrix} 3 & 3\\ 3 & 3\\ \end{bmatrix}
A=
111111
A⊤=[111111]A⊤A=[3333]
此时
A
⊤
A
A^{\top}A
A⊤A不可逆。
性质
N
(
A
⊤
A
)
=
N
(
A
⊤
)
r
a
n
k
(
A
⊤
A
)
=
r
a
n
k
(
A
)
N(A^{\top}A)=N(A^{\top})\\ rank(A^{\top}A)=rank(A)
N(A⊤A)=N(A⊤)rank(A⊤A)=rank(A)
下节再证明吧。







![[React 进阶系列] React Context 案例学习:使用 TS 及 HOC 封装 Context](https://img-blog.csdnimg.cn/direct/f151f858117140628f8fee1c75e3459a.gif#pic_center)

