8. BBDM: Image-to-Image Translation with Brownian Bridge Diffusion Models

  本文提出一种基于布朗桥（Brownian Bridge）的扩散模型用于图像到图像的转换。图像到图像转换的目标是将源域$A$中的图像$I_A$，映射到目标域$B$中得到图像$I_B$。在一般的扩散模型中（如DDPM），是从目标域$B$中采集样本作为起点$x_0$对其进行扩散，得到纯噪声$x_T$；然后，再从纯噪声中采样进行反向去噪，生成目标图像$x_0$。为了实现图像到图像的转换，一般会将参考图像作为条件$y$，引入到生成过程中，噪声估计网络${ϵ}_{\theta }$同时根据前一步的结果$x_t$，时刻$t$和条件$y$来估计噪声，进而得到新的去噪结果$x_{t-1}$，如下图A所示。

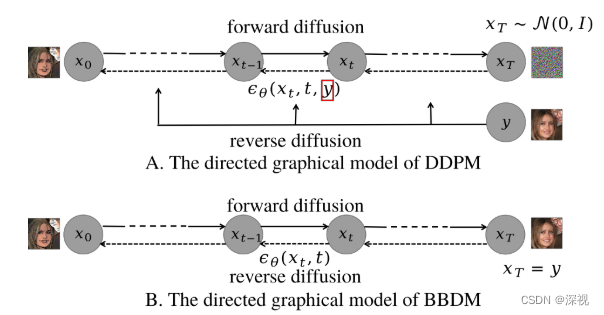
  不同于一般的扩散模型，其扩散过程只依赖于起始点$x_0$，布朗桥扩散过程同时依赖起点$x_0$和终点$x_T$，其数学表达如下$$p\left({\mathbf{x}}_t\mid {\mathbf{x}}_0,{\mathbf{x}}_T\right)=\mathcal{N}\left(\left(1-\frac{t}{T}\right){\mathbf{x}}_0+\frac{t}{T}{\mathbf{x}}_T,\frac{t(T-t)}{T}\mathbf{I}\right)\text{\hspace{1em}(8-1)}$$基于此，作者将条件$y$取代纯噪声作为终点$x_T$，然后从条件$y$开始进行反向去噪得到目标图像$x_0$。值得注意的是，在生成过程中，条件$y$只作为起点，而不作为噪声估计网络${ϵ}_{\theta }$的条件，如上图B所示。
  为了提升学习的效率和泛化能力，作者在浅层空间中完成扩散和重建过程，而不是在图像空间中，作者先利用VQGAN的编码器将图像$I_A$映射到潜在空间中$L_A$，经过扩散和重建后得到目标域的潜在特征$L_{A\to B}$，最后再利用VQGAN的解码器恢复得到图像$I_{A\to B}$。

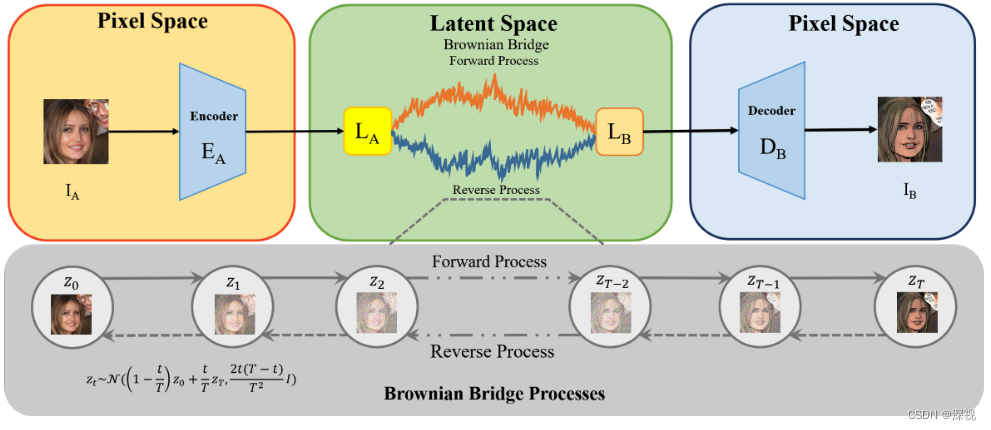
这篇文章我读着很迷惑，从源域转换到目标域，那么根据上图的表示源域应该是真实图片，目标域是漫画图像，那么所谓的条件也就是参考图像$y$应该是来自于源域啊。为什么文章中又说从目标域$B$中采样得到$y$呢？而且前文一直在讲，把$y$作为前向扩散过程的终点和反向去噪过程的起点，那为什么上图灰色区域中前向扩散的终点是目标域的图像呢？不知道是我自己的理解问题，还是作者本身的写作有误。下文会按照我自己的理解来写，可能会与原文有一点点微弱的出入。

  分别从源域$A$和目标域$B$中采集成对的样本$(y,x)$，经过VQGAN的编码器处理后得到对应的特征向量$\mathbf{y},\mathbf{x}$，则布朗桥前向扩散过程可写为$$q_{BB}\left({\mathbf{x}}_t\mid {\mathbf{x}}_0,\mathbf{y}\right)=\mathcal{N}\left({\mathbf{x}}_t;\left(1-m_t\right){\mathbf{x}}_0+m_t\mathbf{y},{\delta }_t\mathbf{I}\right)\text{\hspace{1em}(8-2)}$$其中$${\mathbf{x}}_0=\mathbf{x},m_t=\frac{t}{T}$$$T$表示扩散过程的总步数，方差${\delta }_t$定义为$${\delta }_t=2s\left(m_t-m_t^2\right)\text{\hspace{1em}(8-3)}$$其中$s$作为一个放缩系数，用于控制采样的多样性，默认值为1。这样的设置，保证了当$t=0$和$t=T$时，${\delta }_t$都为0，而$x_t$分别为$x_0$和$y$，满足了前文所述的扩散的起点和终点。扩散过程中单步的转移公式如下$$q_{BB}\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1},\mathbf{y}\right)=\mathcal{N}\left({\mathbf{x}}_t;\frac{1-m_t}{1-m_{t-1}}{\mathbf{x}}_{t-1}+\left(m_t-\frac{1-m_t}{1-m_{t-1}}{m}_{t-1}\right)\mathbf{y},{\delta }_{t\mid t-1}\mathbf{I}\right)\text{\hspace{1em}(8-4)}$$其中$${\delta }_{t\mid t-1}={\delta }_t-{\delta }_{t-1}\frac{{\left(1-m_t\right)}^2}{{\left(1-m_{t-1}\right)}^2}\text{\hspace{1em}(8-5)}$$
  经过前向扩散过程，我们将目标域的图像$x_0$映射到源域中的$x_T=y$，在接下来的反向去噪过程中，我们将从$y$出发逐步去噪生成一个新的目标域图像$x_0$，单步的去噪过程如下$$p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,\mathbf{y}\right)=\mathcal{N}\left({\mathbf{x}}_{t-1};{\mathbf{\mu }}_{\theta }\left({\mathbf{x}}_t,t\right),{\tilde{\delta }}_t\mathbf{I}\right)\text{\hspace{1em}(8-6)}$$其中均值${\mathbf{\mu }}_{\theta }\left({\mathbf{x}}_t,t\right)$是由一个神经网络根据${\mathbf{x}}_t,t$估计得到的，而方差${\tilde{\delta }}_t$则是一个无需学习的仅与$t$有关的变量。那么下面的任务就是如何训练一个网络来估计均值${\mathbf{\mu }}_{\theta }\left({\mathbf{x}}_t,t\right)$了。与DDPM类似，作者也是给出一个了可变分下界的目标函数$$\begin{array}{rl}ELBO& =-{\mathbb{E}}_q(D_{KL}\left(q_{BB}\left({\mathbf{x}}_T\mid {\mathbf{x}}_0,\mathbf{y}\right)\Vert p\left({\mathbf{x}}_T\mid \mathbf{y}\right)\right)\\ & +\sum _{t=2}^T{D}_{KL}\left(q_{BB}\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0,\mathbf{y}\right)\Vert p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,\mathbf{y}\right)\right)\\ & -\log p_{\theta }\left({\mathbf{x}}_0\mid {\mathbf{x}}_1,\mathbf{y}\right))\end{array}\text{\hspace{1em}(8-7)}$$其中第一项为常数，可以忽略。重点看第二项，$q_{BB}\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0,\mathbf{y}\right)$根据贝叶斯理论可得$$\begin{array}{rl}{q}_{BB}\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0,\mathbf{y}\right)& =\frac{q_{BB}\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1},\mathbf{y}\right)q_{BB}\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_0,\mathbf{y}\right)}{q_{BB}\left({\mathbf{x}}_t\mid {\mathbf{x}}_0,\mathbf{y}\right)}\\ & =\mathcal{N}\left({\mathbf{x}}_{t-1};{\tilde{\mathbf{\mu }}}_t\left({\mathbf{x}}_t,{\mathbf{x}}_0,\mathbf{y}\right),{\tilde{\delta }}_t\mathbf{I}\right)\end{array}\text{\hspace{1em}(8-8)}$$其中均值${\tilde{\mathbf{\mu }}}_t\left({\mathbf{x}}_t,{\mathbf{x}}_0,\mathbf{y}\right)$为$$\begin{array}{rl}{\tilde{\mathbf{\mu }}}_t\left({\mathbf{x}}_t,{\mathbf{x}}_0,\mathbf{y}\right)& =\frac{{\delta }_{t-1}}{{\delta }_t}\frac{1-m_t}{1-m_{t-1}}{\mathbf{x}}_t\\ & +\left(1-m_{t-1}\right)\frac{{\delta }_{t\mid t-1}}{{\delta }_t}{\mathbf{x}}_0\\ & +\left(m_{t-1}-m_t\frac{1-m_t}{1-m_{t-1}}\frac{{\delta }_{t-1}}{{\delta }_t}\right)\mathbf{y}\end{array}\text{\hspace{1em}(8-9)}$$方差${\tilde{\delta }}_t$为$${\tilde{\delta }}_t=\frac{{\delta }_{t\mid t-1}\cdot {\delta }_{t-1}}{{\delta }_t}\text{\hspace{1em}(8-10)}$$由于在推理过程中$x_0$是未知的，因此可以根据公式8-2由当前的$x_t$反向估计一个${\hat{x}}_0$，将其带入公式8-9中可得$${\tilde{\delta }}_t=\frac{{\delta }_{t\mid t-1}\cdot {\delta }_{t-1}}{{\delta }_t}{\tilde{\mathbf{\mu }}}_t\left({\mathbf{x}}_t,\mathbf{y}\right)=c_{xt}{\mathbf{x}}_t+c_{yt}\mathbf{y}+c_{ϵt}\left(m_t\left(\mathbf{y}-{\mathbf{x}}_0\right)+\sqrt{{\delta }_t}\mathbf{ϵ}\right)\text{\hspace{1em}(8-11)}$$其中$$\begin{array}{l}{c}_{xt}=\frac{{\delta }_{t-1}}{{\delta }_t}\frac{1-m_t}{1-m_{t-1}}+\frac{{\delta }_{t\mid t-1}}{{\delta }_t}\left(1-m_{t-1}\right)\\ c_{yt}=m_{t-1}-m_t\frac{1-m_t}{1-m_{t-1}}\frac{{\delta }_{t-1}}{{\delta }_t}\\ c_{ϵt}=\left(1-m_{t-1}\right)\frac{{\delta }_{t\mid t-1}}{{\delta }_t}\end{array}\text{\hspace{1em}(8-12)}$$与DDPM中一样，作者不直接预测均值${\tilde{\mu }}_t$，而是对其中的噪声$ϵ$进行预测。$p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,\mathbf{y}\right)$中的均值项${\mathbf{\mu }}_{\theta }\left({\mathbf{x}}_t,t\right)$可以重写为${\mathbf{x}}_t,\mathbf{y}$和估计噪声${ϵ}_{\theta }$的线性组合$${\mathbf{\mu }}_{\mathbf{\theta }}\left({\mathbf{x}}_t,\mathbf{y},t\right)=c_{xt}{\mathbf{x}}_t+c_{yt}\mathbf{y}+c_{ϵt}{\mathbf{ϵ}}_{\theta }\left({\mathbf{x}}_t,t\right)\text{\hspace{1em}(8-13)}$$则目标函数$ELBO$可以简化为$${\mathbb{E}}_{{\mathbf{x}}_0,\mathbf{y},\mathbf{ϵ}}\left[c_{ϵt}{\Vert m_t\left(\mathbf{y}-{\mathbf{x}}_0\right)+\sqrt{{\delta }_t}\mathbf{ϵ}-{\mathbf{ϵ}}_{\theta }\left({\mathbf{x}}_t,t\right)\Vert }^2\right]\text{\hspace{1em}(8-14)}$$
完整的训练流程如下

  经过训练得到噪声估计网络${\mathbf{ϵ}}_{\theta }\left({\mathbf{x}}_t,t\right)$，就可以从源域中任意采样一个条件输入$\mathbf{y}$作为生成的起点${\mathbf{x}}_T$，经过反向去噪得到生成结果$x_0$，如下所示

  上述的采样过程也可以利用DDIM提出的加速技巧进行加速。整体上而言，BBDM就是将原本扩散过程从图像到噪声的变换，改成了从目标图像到源图像的变换。然后，在反向去噪时，只需给定一个源图像就能据此生成对应目标域中的样本。虽然不用像其他条件扩散模型那样，将条件引入模型中用于训练，但在BBDM的训练过程需要成对的样本，这限制了BBDM在许多情景中的应用。