学这东西主要是 这道题 要用 233

定义：给定两个凸包$A$,$B$，定义 C = { a + b ∣ a ∈ A , b ∈ B } C=\{a+b|a\in A,b\in B\} C={a+b∣a∈A,b∈B} ，其中$a$,$b$均为坐标。

不好意思图是嫖的

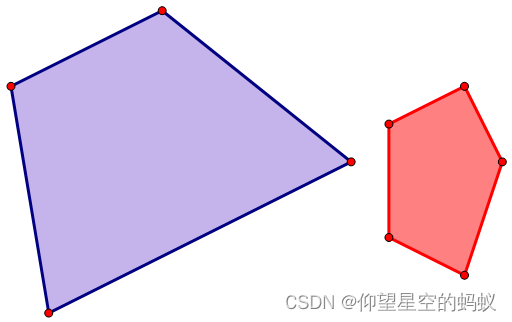
首先我们感性认识一下。可以直接将一个凸包的顶点换成另一个凸包，然后保留外层凸包。

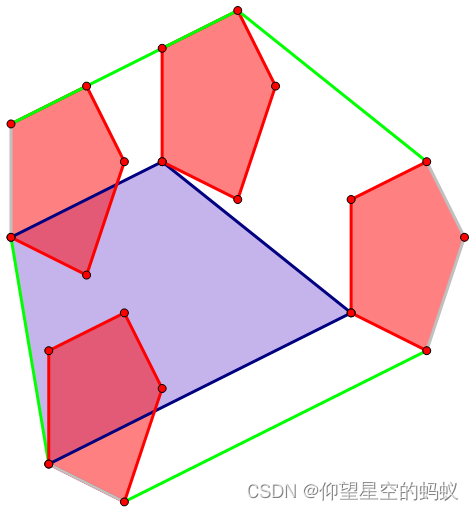
于是我们看出来合并后凸包大小为$|A|+|B|$。可以看成从一个凸包跳到另一个凸包再跳回来。

对于下凸壳闵可夫斯基和，下凸壳就是凸壳下部分的点集，可以看成被下方平行光照射的部分。

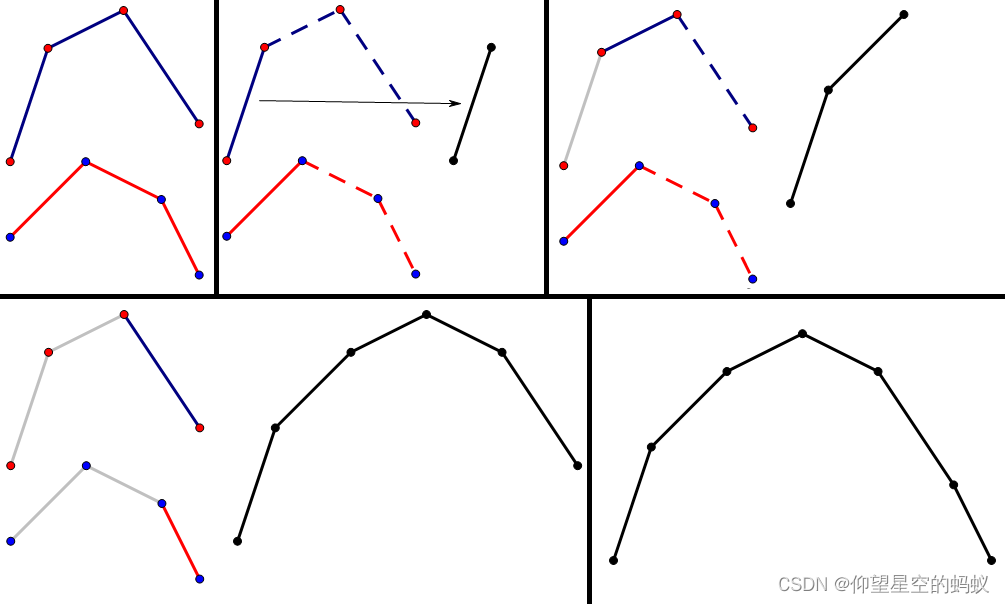
可以发现其本质就是差分数组合并后的结果。复杂度$O(|A|+|B|)$。

回到 假人 这道题。我们知道结论$f(i)$按模$12$分组构成凸包，这启发我们采用分治算法，用闵可夫斯基和将左右凸包两两合并即可。

代码咕了。

代码来了。借鉴了一下std的做法。

#include<bits/stdc++.h>
#define fi first
#define se second
#define ll long long
#define pb push_back
#define db double
#define mp make_pair
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
int n,m,ps[100005];
vector<int>a[100005];
struct Data{
	vector<ll>vec[12];
};
void chmax(ll &x,ll y){x=max(x,y);}
inline void Merge(const Data &a, const Data &b, Data &c) {
	for (int i = 0; i < 12; i++) if (a.vec[i].size()) {
		for (int j = 0; j < 12; j++) if (b.vec[j].size()) {
			int dlt = (i + j >= 12), k = (i + j) % 12;
			int x = 0, y = 0;
			while (true) {
				chmax(c.vec[k][x + y + dlt], a.vec[i][x] + b.vec[j][y]);
				if (x == (int)a.vec[i].size() - 1 && y == (int)b.vec[j].size() - 1) break;
				if (x == (int)a.vec[i].size() - 1) y++;
				else if (y == (int)b.vec[j].size() - 1) x++;
				else {
					if (a.vec[i][x + 1] - a.vec[i][x] > b.vec[j][y + 1] - b.vec[j][y]) x++;
					else y++;
				}
			}
		}
	}
}
Data solve(int l, int r) {
	if (l == r) {
		Data ret;
		for (int i = 0; i < (int)a[l].size(); i++) ret.vec[i].push_back(a[l][i]);
		return ret;
	}
	int mid = (l + r) >> 1;
	Data a = solve(l, mid), b = solve(mid + 1, r), ret;
	for (int i = 0; i < 12; i++) {
		for (int j = i; j <= ps[r] - ps[l - 1]; j += 12) {
			ret.vec[i].push_back(-1);
		}
	}
	Merge(a, b, ret);
	return ret;
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	cin>>n;for(int i=1;i<=n;i++){
		int k;cin>>k,m+=k,ps[i]=ps[i-1]+k-1;for(int j=0;j<k;j++){
			int x;cin>>x,a[i].pb(x);
		}
	}Data res=solve(1,n);
	for(int i=0;i<=m-n;i++)cout<<res.vec[i%12][i/12]<<" ";
}