目录

思想：

源码：

---

思想：

计数排序：用一个数组记录按原始数据中，每个数据出现的次数
非常牛批的思路，没有用到比较
直接对每个数据进行计数
然后从计数的数组中，往回覆盖数据
从左到右，依次打印次数个数据，打完数据，整个排序就好了 
一组数据，开出和数据组相对应的count空间大小，作为映射，来对每个数据出现的次数记录
计数排序，总的思路来说就是
在原来数组的基础上，开出一个新的数组，空间一样
然后，遍历原来的数组，对原来数组的每一个数据进行记录
然后将之在count数组对应的位置+1，在遍历的过程中每遇到一次，就对该位置+1
这才是精髓之所在！
这是第一步
然后进行第二步
就是对count数组进行遍历
对应位置出现的数据，下标是原来数据的值，count数组中记录的值是原来数据值得个数
遍历count数组，将对应的数据覆盖回原来的数组之中

计数排序的效率：极高！O(aN + countN)
第一次遍历数组a，第二次遍历count
局限性：
1、不适合数据很分散的数据序列，更适合比较集中的数据
2、不适合浮点数、字符串、结构体等数据排序，只适合整数
还有一个问题：
例如说，一组数据从99999到100000
那么，如果是开出一组绝对映射的count数组，那么前面的99999空间就是纯粹的浪费
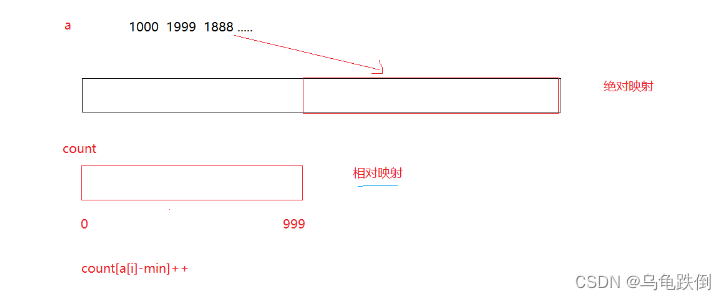
所以，我们用相对映射
最小的值放在左边
count[a[i] - min]++;//吧对应的值放在对应的位置，非常巧妙、
不是直接位置，而是间接位置

同时，相对映射正好可以完美的解决负数的问题

时间复杂度：O(N+range)
空间:O(range)
n--走n次
--n走n-1次

在现实生活中，一般比较的都是结构体

源码：

//计数排序
void CountSort(int* a, int n)
{
	
	int min = a[0], max = a[0];
	for (int i = 0; i < n; i++)
	{
		if (a[i] < min)
		{
			min = a[i];
		}
		if (a[i] > max)
		{
			max = a[i];
		}
	}

	int range = max - min + 1;//左闭右闭
	int* count = (int*)calloc(range, sizeof(int));
	if (count == NULL)
	{
		perror("calloc fail");
		return;
	}


	for (int i = 0;i < n;++i)
	{
		count[ a[i] - min]++;//对数组a对应位置的数据记录到count数组
	}

	//排序
	int i = 0;
	for (int j = 0;j<range;++j)
	{
		while (count[j]--)
		{
			a[i++] = j + min;
		}
	}

}