组合

77. 组合 - 力扣（LeetCode）

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

解

public List<List<Integer>> combine(int n, int k)
{
    List<List<Integer>> resList = new ArrayList<>();
    Deque<Integer> paths = new ArrayDeque<>();
    //数字集[1,n],每条路径有k个数
    dfs(n, k, 1, paths, resList);

    return resList;
}

public void dfs(int n, int k, int startIndex, Deque<Integer> paths, List<List<Integer>> resList)
{
    if (paths.size() == k)
    {
        resList.add(new ArrayList<>(paths));
        return;
    }

    for (int i = startIndex; i <= n; i++)
    {
        paths.addLast(i);
        dfs(n, k, i + 1, paths, resList);
        //回溯清除
        paths.removeLast(); //双端列表才有的方法
    }
}

二叉树的所有路径

257. 二叉树的所有路径 - 力扣（LeetCode）

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

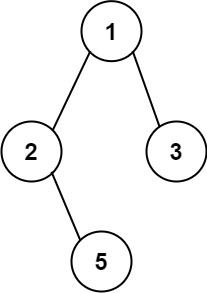
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

从回溯的角度看之前的代码

String ans的值传递特性，帮我们实现了回溯的关键一步：撤销。

public void preOrder(TreeNode root, List<String> list, String ans)
{
    if (root == null)
        return;

    //找到一个叶子结点后，将路径添加到列表，返回
    if (root.left == null && root.right == null)
    {
        ans = ans + String.format("%s",root.val);
        list.add(ans);
        return;
    }

    //保存路径上的节点
    ans = ans + String.format("%s->",root.val);

    preOrder(root.left, list, ans);
    preOrder(root.right, list, ans);
}

路径总和 II

113. 路径总和 II - 力扣（LeetCode）

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

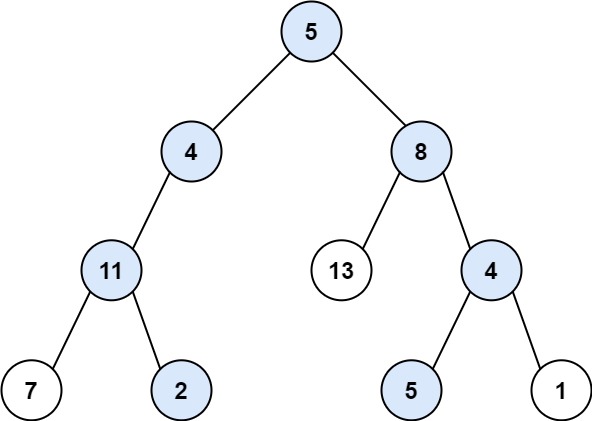
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

解

static List<List<Integer>> resPaths = new ArrayList<>();

public static List<List<Integer>> pathSum(TreeNode root, int targetSum)
{
    LinkedList<Integer> path = new LinkedList<>();
    dfs(root, targetSum, path);
    return resPaths;
}

public static void dfs(TreeNode root, int targetSum, LinkedList<Integer> path)
{
    if (root == null)
        return;

    targetSum -= root.val;
    path.add(root.val);

    if (targetSum == 0 && root.left == null && root.right == null)
        resPaths.add(new ArrayList<>(path));

    dfs(root.left, targetSum, path);
    dfs(root.right, targetSum, path);

    path.removeLast();  //撤销当前访问的结点，回溯到上一层，访问、添加下一个结点
}