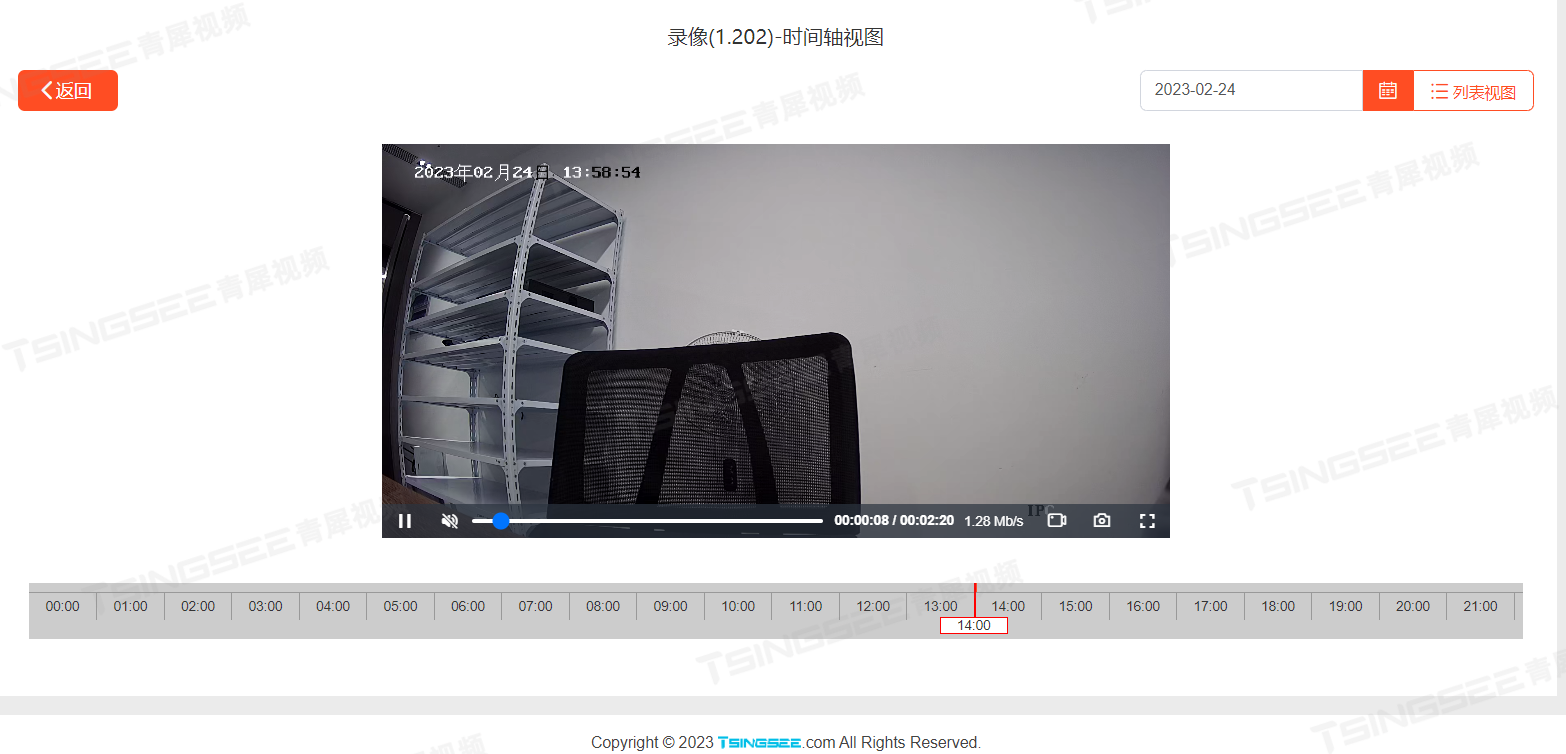
作者推荐

视频算法专题

本文涉及知识点

动态规划汇总

优化动态规划的时间复杂度，主要有如下几种：

一，不同的状态表示。

比如：n个人，m顶帽子。
第一种方式：dp[i][mask] ,i表示前i个人已经选择帽子，mask 表示 那些帽子已经选择。 空间复杂度：O(n2^m)。
第二种方式：dp[i][mask] ,i表示前i个帽子已经选择，mask表示那些人已经选择。 空间复杂度：O(m2²)。
n大，则现在方式一；否则选择方式二。

【状态压缩】【动态规划】【C++算法】1125.最小的必要团队

二，通过优化状态减少状态数

例一

【动态规划】【C++算法】2518. 好分区的数目
num的长度$\in$[1,1000],num[i]$\in$[0,10⁶] k$\in$[0,1000]。
将num的元素放到两个数组中，两个数组的和都为k。
由于num[i] >=0，所以 数组和已经大于k 的无论如何都不会等于k，抛弃。
dp[k1][k2] 的状态数是固定。
$$当处理完num[0,i)时,两个数组的和是固定⟺k1+k2\equiv \sum {}_{j:0}^{i-1}nums[j]$$
我记录k1或k2就可以了。新问题是k1 可能是5e8。
$$\{\begin{array}{ll}k1& k1<k\\ -min(k2,k)& else\end{array}$$

例子二

2742. 给墙壁刷油漆
付费工人，各任务用时time[i]，免费工人用时1，time.length$\in$[1,500]。付费工人用时和必须大于等于免费工人用时。如果分别记录付费工人和免费工人用时，则状态数：500*500。
付费工人用时和必须大于等于免费工人 $⟺$ (statu = 付费工人用时 - 免费工人用时) >= 0
statu $\in$ [-500,500] 可以记录状态的时候+500，解析状态的时候再-500。

三 通过优化转移方程

转移方程主要有两种：
a，枚举前置状态，更新后置状态。除剪枝小幅提升性能外，暂时没发现优化方法。
b,枚举后置状态，通过前置状态计算后置状态。利用前缀和、极值、优先队列（堆）、单调栈（队列、向量）、预处理 等优化。

2617 网格图中最少访问的格子数	两种方法：分别用单调栈、优先队列优化
【动态规划】【滑动窗口】【C++算法】 629K 个逆序对数组	前缀和
【动态规划】【状态压缩】【2次选择】【广度搜索】1494. 并行课程 II	枝小幅提升性能
【动态规划】【C++算法】1563 石子游戏 V	极值

四 匹配无限次可以拆分成匹配0次和1次

以通配符为例。
abc 匹配 *
初始匹配长度0
处理* ：
长度0的后置状态：*不匹配任何字符，匹配长度0。
长度0的后置状态：*匹配一个字符，匹配长度1。
长度1的后置状态：*不匹配任何字符，匹配长度1。
长度1的后置状态：*匹配一个字符，匹配长度2。
$⋮$
总计： *可以匹配0到无限字符，才可以这样处理。 .只能匹配一个字符不能这样处理。

【动态规划】【字符串】C++算法：正则表达式匹配

【状态压缩】【动态规划】【C++算法】691贴纸拼词
【动态规划】【数学】【C++算法】1449. 数位成本和为目标值的最大数字
【动态规划】【C++算法】2188. 完成比赛的最少时间

五 逆向思考

【动态规划】【 矩阵】【逆向思考】C++算法174地下城游戏
正向思考：要记录进入(r,c)后的健康，还有记录初始健康。比如：路径一： 3 $\to$ -2 ，初始只需要1，最终健康2。
路径二： -1 $\to$ 4 ，初始要求 2，最终健康度 5。如果终点格是-1,前者能过。 如果是-4，后者能过。前者需要4，才能过。
$$\{\begin{array}{ll}路径一初始1，路径二初始2& 终点<-1\\ 路径一初始4，路径二初始2& 终点-4\end{array}$$

【动态规划】【C++算法】741摘樱桃

六 去掉重复

【动态规划】C++算法：403.青蛙过河

扩展阅读

视频课程

有效学习：明确的目标 及时的反馈 拉伸区（难度合适），可以先学简单的课程，请移步CSDN学院，听白银讲师（也就是鄙人）的讲解。
https://edu.csdn.net/course/detail/38771

如何你想快速形成战斗了，为老板分忧，请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176

相关

下载

想高屋建瓴的学习算法，请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653

我想对大家说的话
闻缺陷则喜是一个美好的愿望，早发现问题，早修改问题，给老板节约钱。
子墨子言之：事无终始，无务多业。也就是我们常说的专业的人做专业的事。
如果程序是一条龙，那算法就是他的是睛

测试环境

操作系统：win7 开发环境： VS2019 C++17
或者 操作系统：win10 开发环境： VS2022 **C+

+17**
如无特殊说明，本算法用**C++**实现。