电力系统强大的Gurobi 求解器的学习（PythonMatlab）

到底有多强大，看看就知道，必须👍👍👍：

1 概述

2 算例理解【Python】

2.1 算例1——详细入门

2.2 算例2——一般线性规划问题

2.3 算例3——非凸问题

3 算例升级【Matlab】

3.1 模型

3.2 电力系统经济调度（Matlab代码实现）[Yalmip + Gurobi]

4 致谢

1 概述

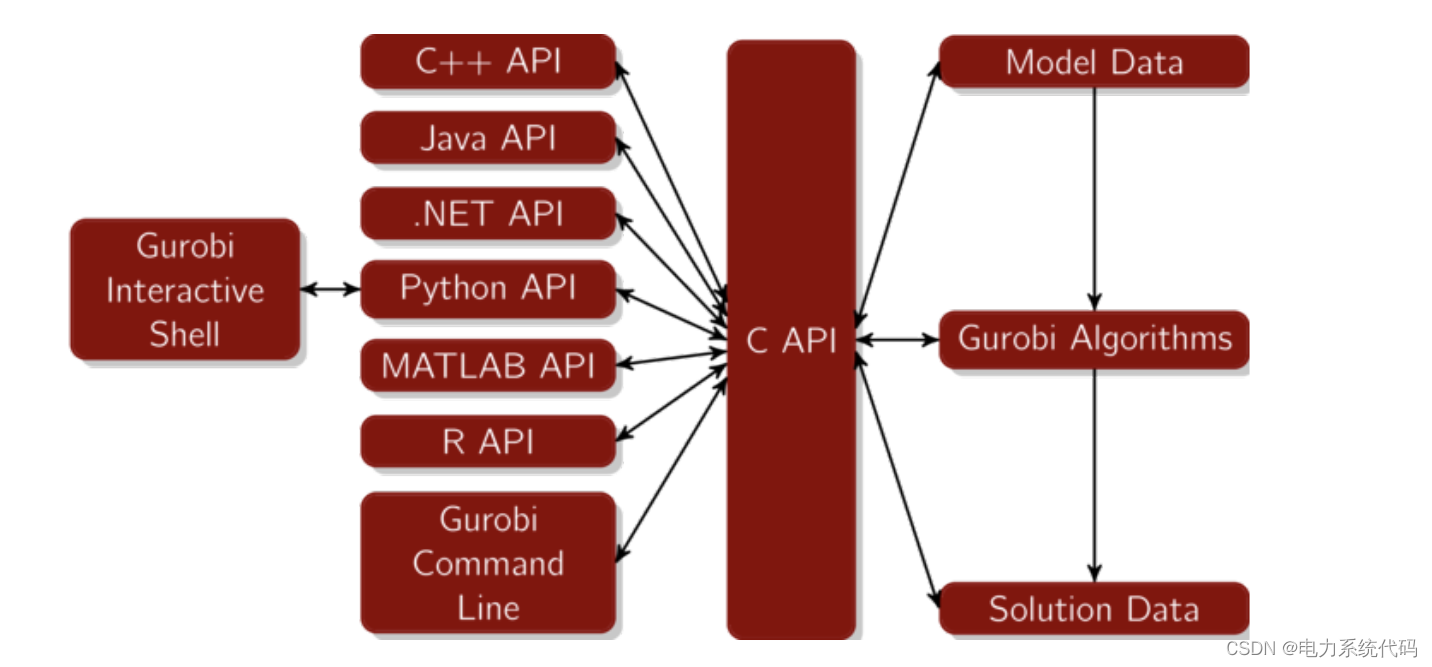
我们经常提到优化模型的类。具有线性目标函数、线性约束和连续变量的模型是线性程序（LP）。如果目标是二次型，则模型是二次程序（QP）。如果任何约束是二次的，则模型是二次约束程序（QCP）。我们有时会提到QCP的一些特殊情况：具有凸约束的QCP，具有非凸约束的QCP，双线性程序和二阶锥程序（SOCP）。如果模型包含任何整数变量、半连续变量、半整数变量、特殊有序集（SOS）约束或常规约束，则该模型是混合整数程序（MIP）。我们有时还会讨论MIP的特殊情况，包括混合整数线性程序（MILP），混合整数二次程序（MIQP），混合整数二次约束程序（MIQCP）和混合整数二阶锥程序（MISOCP）。Gurobi Optimizer 处理所有这些模型类。

Gurobi Python接口中的大多数操作都是通过在Gurobi对象上调用方法来执行的。最常用的对象是模型。模型由一组决策变量（类 Var 或 MVar 的对象）、这些变量上的线性或二次目标函数（使用 Model.setObjective 指定）和这些变量上的一组约束（类 Constr、MConstr、QConstr、SOS 或 GenConstr 的对象）组成).每个变量都有关联的下限、上限和类型（连续、二进制等）。每个线性或二次约束都有一个关联的意义（小于或等于、大于或等于或等于）和右侧值。有关变量、约束和目标的详细信息，请参阅本节。

优化模型可以通过从文件加载模型（使用前面提到的读取函数）一次性全部指定，也可以增量构建，方法是首先构造类 Model 的空对象，然后调用 Model.addVar、Model.addVars 或 Model.addMVar 来添加其他变量，以及 Model.addConstr、Model.addConstrs、Model.addLConstr、Model.addQConstr、 Model.addSOS，或任何 Model.addGenConstrXxx 方法来添加其他约束。

生成模型后，可以调用 Model.optimize 来计算解决方案。默认情况下，optimize 将使用并发优化器求解 LP 模型，使用势垒算法求解具有凸目标的 QP 模型和具有凸约束的 QCP 模型，否则将使用分支和切割算法。该解决方案存储在模型的一组属性中，可以随后查询这些属性（我们稍后将返回到本主题）。

Gurobi 算法会仔细跟踪模型的状态，因此，如果自上次优化模型以来相关数据已更改，则对 Model.optimize 的调用才会执行进一步的优化。如果要放弃以前计算的解决方案信息，并在不更改模型的情况下从头开始优化，可以调用 Model.reset。

求解 MIP 模型后，可以调用 Model.fixed 来计算关联的固定模型。此模型与原始模型相同，只是整数变量固定在 MIP 解决方案中的值。如果模型包含 SOS 约束，则这些约束中出现的一些连续变量也可能是固定的。在某些应用程序中，计算此固定模型上的信息（例如，对偶变量、灵敏度信息等）可能很有用，尽管在解释此信息时应小心谨慎。

2 算例理解【Python】

2.1 算例1——详细入门

2.1.1 算例

为了清晰明了，公式得纯手打：

$\begin{array}{ll} \min & w \\ \text { s.t. } & (x-1)^{2}+(y-1)^{2}-1 \leqslant 0 \\ & z+y-2 \leqslant 0 \\ & z=|x| \\ & u=y+4 \\ & w=\max \{z, u\} \\ & w, z \geqslant 0 \end{array}$

2.1.2 Python代码实现

这里为了方便讲解，这样安排：

'''======1.导入相关库========'''
from gurobipy import *

'''======2.创建模型=========='''
#MODEL = gurobipy.Model("Model_name")
#或者 model = Model('name_')也可以这样。
model = Model('nonlinear example')  #非线性规划

'''======3.创建变量============='''
#    (1)lb=0.0，变量的下界，默认为0；
#    (2)ub=GRB.INFINITY，变量的上界，默认为无穷；
#    (3)vtype，变量的类型，默认为连续型，可改为 GRB.BINARY 0-1变量；GRB.INTEGER 整型；name=”“，变量名，默认为空。
w = model.addVar(lb=0, ub=GRB.INFINITY, vtype=GRB.CONTINUOUS, name='w')
z = model.addVar(lb=0, ub=GRB.INFINITY, vtype=GRB.CONTINUOUS, name='z')
x = model.addVar(lb=-GRB.INFINITY, ub=GRB.INFINITY, vtype=GRB.CONTINUOUS, name='x')
y = model.addVar(lb=-GRB.INFINITY, ub=GRB.INFINITY, vtype=GRB.CONTINUOUS, name='y')
u = model.addVar(lb=-GRB.INFINITY, ub=GRB.INFINITY, vtype=GRB.CONTINUOUS, name='u')

'''=====4..更新变量空间========='''
model.update()

'''=======5.目标函数============'''
# 单目标： MODEL.setObjective(expression, sense=None) sense可用选择：GRB.MINIMIZE/GRB.MAXIMIZE
# 多目标：MODEL.setObjectiveN(expression, index, priority=0, weight=1.0, abstol=0, reltol=0, name="")
# expression: 表达式，可以是一次或二次函数类型,目标函数
# index: 目标函数对应的序号 (默认 0，1，2，…), 以 index=0 作为目标函数的值, 其余值需要另外设置参数
# priority: 分层序列法多目标决策优先级(整数值), 值越大优先级越高
# weight: 线性加权多目标决策权重(在优先级相同时发挥作用)
# abstol: 分层序列法多目标决策时允许的目标函数值最大的降低量
# reltol: 分层序列法多目标决策时允许的目标函数值最大的降低比率 reltol*|目标函数值|
model.setObjective(w, GRB.MINIMIZE)

'''========6.约束条件================='''
# 表达式约束： model.addConstr(expression, name="")
# 范围约束：model .addRange(expression, min_value, max_value, name="")
# 指示变量约束，指示变量 binvar 的值取 binval 时, 进行约束 expression: MODEL.addGenConstrIndicator(binvar, binval, expression, name="")
# addQConstr: 添加二次约束
# addGenConstrAbs: 添加绝对值约束，也可以用abs_(x)
# addGenConstrMax：添加max ⁡ \maxmax约束，也可以用max_(z, u)

model.addQConstr(x*x - 2 * x + 1 + y*y - 2*y + 1 - 1 <= 0)
# 或者可以是 model.addConstr(x*x - 2 * x + 1 + y*y - 2*y + 1 - 1 <= 0)
model.addConstr(z + y - 2 <= 0)
model.addGenConstrAbs(z, x)
# 或者可以是 model.addConstr(z == abs_(x))
model.addConstr(u == y + 4)
model.addGenConstrMax(w, (z, u))
# 或者可以是 model.addConstr(w == max_(z, u))
# 或者可以是 model.addConstr(z == max_([z, u]))

'''======7.求解优化问题========'''
# 输出：model.write('VRPTW1.lp')
# 求解：model.optimize()
model.optimize()

'''=======8.输出结果============='''
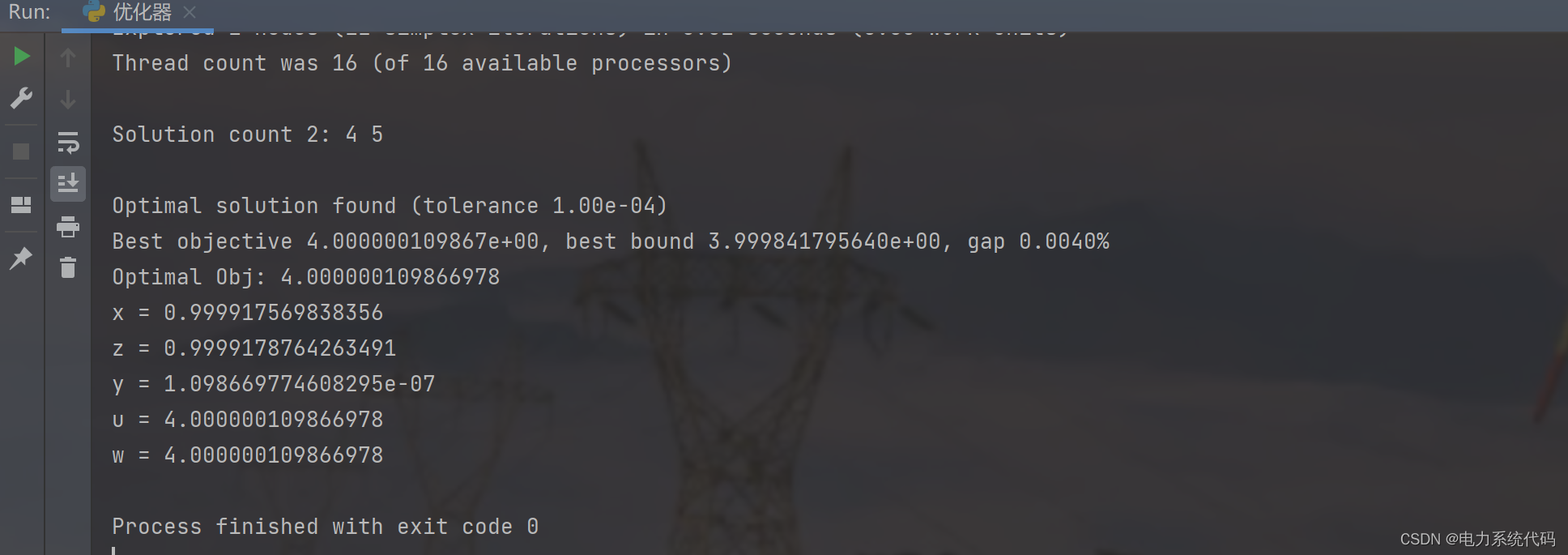
print('Optimal Obj: {}'.format(model.ObjVal))
print('x = {}'.format(x.x))
print('z = {}'.format(z.x))
print('y = {}'.format(y.x))
print('u = {}'.format(u.x))
print('w = {}'.format(w.x))

'''======1.导入相关库========'''
from gurobipy import *

'''======2.创建模型=========='''
#MODEL = gurobipy.Model("Model_name")
#或者 model = Model('name_')也可以这样。
model = Model('nonlinear example')  #非线性规划

'''======3.创建变量============='''
#    (1)lb=0.0，变量的下界，默认为0；
#    (2)ub=GRB.INFINITY，变量的上界，默认为无穷；
#    (3)vtype，变量的类型，默认为连续型，可改为 GRB.BINARY 0-1变量；GRB.INTEGER 整型；name=”“，变量名，默认为空。
w = model.addVar(lb=0, ub=GRB.INFINITY, vtype=GRB.CONTINUOUS, name='w')
z = model.addVar(lb=0, ub=GRB.INFINITY, vtype=GRB.CONTINUOUS, name='z')
x = model.addVar(lb=-GRB.INFINITY, ub=GRB.INFINITY, vtype=GRB.CONTINUOUS, name='x')
y = model.addVar(lb=-GRB.INFINITY, ub=GRB.INFINITY, vtype=GRB.CONTINUOUS, name='y')
u = model.addVar(lb=-GRB.INFINITY, ub=GRB.INFINITY, vtype=GRB.CONTINUOUS, name='u')

'''=====4..更新变量空间========='''
model.update()

'''=======5.目标函数============'''
# 单目标： MODEL.setObjective(expression, sense=None) sense可用选择：GRB.MINIMIZE/GRB.MAXIMIZE
# 多目标：MODEL.setObjectiveN(expression, index, priority=0, weight=1.0, abstol=0, reltol=0, name="")
# expression: 表达式，可以是一次或二次函数类型,目标函数
# index: 目标函数对应的序号 (默认 0，1，2，…), 以 index=0 作为目标函数的值, 其余值需要另外设置参数
# priority: 分层序列法多目标决策优先级(整数值), 值越大优先级越高
# weight: 线性加权多目标决策权重(在优先级相同时发挥作用)
# abstol: 分层序列法多目标决策时允许的目标函数值最大的降低量
# reltol: 分层序列法多目标决策时允许的目标函数值最大的降低比率 reltol*|目标函数值|
model.setObjective(w, GRB.MINIMIZE)

'''========6.约束条件================='''
# 表达式约束： model.addConstr(expression, name="")
# 范围约束：model .addRange(expression, min_value, max_value, name="")
# 指示变量约束，指示变量 binvar 的值取 binval 时, 进行约束 expression: MODEL.addGenConstrIndicator(binvar, binval, expression, name="")
# addQConstr: 添加二次约束
# addGenConstrAbs: 添加绝对值约束，也可以用abs_(x)
# addGenConstrMax：添加max ⁡ \maxmax约束，也可以用max_(z, u)

model.addQConstr(x*x - 2 * x + 1 + y*y - 2*y + 1 - 1 <= 0)
# 或者可以是 model.addConstr(x*x - 2 * x + 1 + y*y - 2*y + 1 - 1 <= 0)
model.addConstr(z + y - 2 <= 0)
model.addGenConstrAbs(z, x)
# 或者可以是 model.addConstr(z == abs_(x))
model.addConstr(u == y + 4)
model.addGenConstrMax(w, (z, u))
# 或者可以是 model.addConstr(w == max_(z, u))
# 或者可以是 model.addConstr(z == max_([z, u]))

'''======7.求解优化问题========'''
# 输出：model.write('VRPTW1.lp')
# 求解：model.optimize()
model.optimize()

'''=======8.输出结果============='''
print('Optimal Obj: {}'.format(model.ObjVal))
print('x = {}'.format(x.x))
print('z = {}'.format(z.x))
print('y = {}'.format(y.x))
print('u = {}'.format(u.x))
print('w = {}'.format(w.x))

2.1.3 结果：

2.2 算例2——一般线性规划问题

2.2.1 算例

$\begin{array}{cl} \min & Z=8 x_{1}+10 x_{2}+7 x_{3}+6 x_{4}+11 x_{5}+9 x_{6} \\ \mathrm{s.t.} & 12 x_{1}+9 x+25 x_{3}+20 x_{4}+17 x_{5}+13 x_{6} \geq 60 \\ & 35 x_{1}+42 x_{2}+18 x_{3}+31 x_{4}+56 x_{5}+49 x_{6} \geq 150 \\ & 37 x_{1}+53 x_{2}+28 x_{3}+24 x_{4}+29 x_{5}+20 x_{6} \geq 125 \\ & 0 \leq x_{j} \leq 1, j=1,2, \cdots, 6 \end{array}$

2.2.2 Python代码实现

#====导入相关库=======
import gurobipy

#====创建模型=======
c = [8, 10, 7, 6, 11, 9]
p = [[12, 9, 25, 20, 17, 13],
	[35, 42, 18, 31, 56, 49],
	[37, 53, 28, 24, 29, 20]]
r = [60, 150, 125]
MODEL = gurobipy.Model("Example")

#=====创建变量===========
x = MODEL.addVars(6, lb=0, ub=1, name='x')

#====更新变量环境=====
MODEL.update()

#========创建目标函数============
MODEL.setObjective(x.prod(c), gurobipy.GRB.MINIMIZE)

#=======创建约束条件=============
MODEL.addConstrs(x.prod(p[i]) >= r[i] for i in range(3))

#======执行线性规划模型=================
MODEL.optimize()
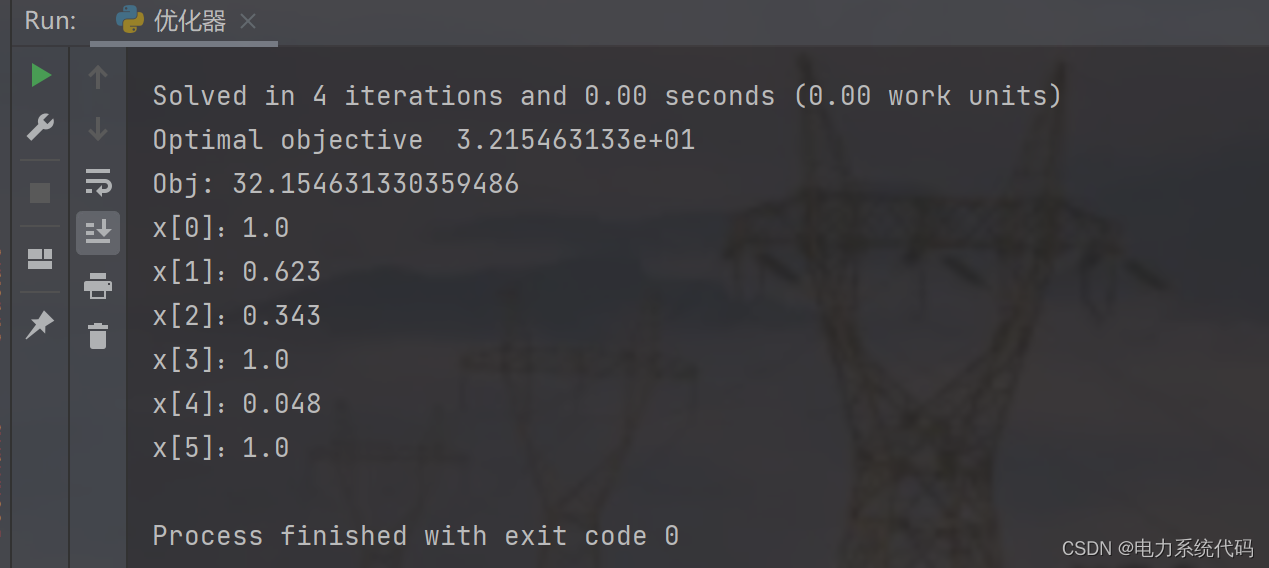
print("Obj:", MODEL.objVal)
for v in MODEL.getVars():
	print(f"{v.varName}：{round(v.x,3)}")  # 查看变量取值，格式模板

2.2.3 结果

2.3 算例3——非凸问题

估计您有点疲倦了，欣赏几个小图：

🚀🚀🚀🍉🍉🍉🌟🌟🌟✨✨✨🍒🍒🍒🏆🏆🏆😜😜😜🌈🌈🌈💕💕💕💓💓

2.3.1 算例

$\begin{array}{ll} \min & 1 \\ s . t . & m_{1}+m_{2}+m_{3}=4 \\ & x_{1}=m_{1}\left(x_{2}+x_{3}\right) \\ & x_{2}=m_{2}\left(x_{1}+x_{3}\right) \\ & x_{3}=m_{2}\left(x_{1}+x_{2}\right) \\ & m_{i} \geqslant 0, \quad \forall i=1,2,3 \\ & x_{i} \geqslant 1, \quad \forall i=1,2,3 \\ & x_{i} \in \mathbb{Z}, \quad \forall i \in 1,2,3 \end{array}$

2.3.2 python代码实现

#===导入相关库==========
from gurobipy import *

#===创建模型============
m = Model("feitu")
m.setParam('NonConvex', 2) #非凸模型求解参数

#====创建变量=============
x1  = m.addVar(lb=0, vtype=GRB.INTEGER, name="x1")
x2  = m.addVar(lb=0, vtype=GRB.INTEGER, name="x2")
x3  = m.addVar(lb=0, vtype=GRB.INTEGER, name="x3")
m1 = m.addVar(lb=0, vtype=GRB.CONTINUOUS, name="m1")
m2 = m.addVar(lb=0, vtype=GRB.CONTINUOUS, name="m2")
m3 = m.addVar(lb=0, vtype=GRB.CONTINUOUS, name="m3")

#==========约束条件============
m.addConstr(x1 >= 1, "c1")  #x1,x2,c为正整数
m.addConstr(x2 >= 1, "c1")
m.addConstr(x3 >= 1, "c1")
m.addConstr(x1 == m1 * (x2 + x3))
m.addConstr(x2 == m2 * (x1 + x3))
m.addConstr(x3 == m3 * (x1 + x2))
m.addConstr(m1 + m2 + m3 - 4 == 0)

#=========目标函数===========
m.setObjective(1, GRB.MINIMIZE)
m.optimize()

#======结果输出===========
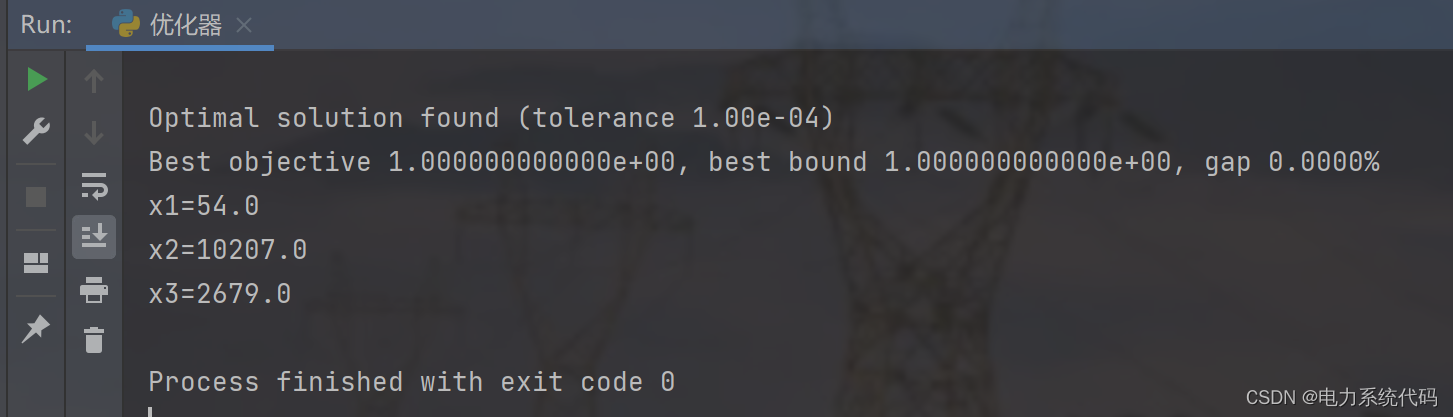
print('x1={} '.format(x1.x))
print('x2={} '.format(x2.x))
print('x3={} '.format(x3.x))

2.3.3 结果

3 算例升级【Matlab】

3.1 模型

我们的 Gurobi MATLAB 界面使您能够表达以下形式的问题：

模型存储为结构变量，每个变量由多个字段组成。这些字段捕获上面列出的不同模型组件。其中许多模型组件是可选的。例如，可以省略完整性约束。

优化模型可以从文件加载（使用gurobi_read函数），也可以通过填充模型变量的相应字段（使用标准 MATLAB 构造）来构建。我们将在模型参数部分中讨论如何表示模型的详细信息。

我们经常提到优化模型的类。具有线性目标函数、线性约束和连续变量的模型是线性程序（LP）。如果目标是二次型，则模型是二次程序（QP）。如果任何约束是二次的，则模型是二次约束程序（QCP）。我们有时会提到QCP的一些特殊情况：具有凸约束的QCP，具有非凸约束的QCP，双线性程序和二阶锥程序（SOCP）。如果模型包含任何整数变量、半连续变量、半整数变量、特殊有序集（SOS）约束或常规约束，则该模型是混合整数程序（MIP）。我们有时还会讨论MIP的特殊情况，包括混合整数线性程序（MILP），混合整数二次程序（MIQP），混合整数二次约束程序（MIQCP）和混合整数二阶锥程序（MISOCP）。Gurobi Optimizer 处理所有这些模型类。

求解模型

构建模型后，可以调用 gurobi 来计算解决方案。默认情况下，gurobi 将使用并发优化器求解 LP 模型，使用势垒算法求解 QP 模型和具有凸约束的 QCP 模型，并使用分支和切割算法求解混合整数模型。解决方案作为结构变量返回。当我们讨论gurobi函数时，我们将讨论如何表示优化结果的细节。

以下是MATLAB API中可能命令序列的简单示例：
model = gurobi_read（'examples/data/stein9.mps'）;
result = gurobi（model）;

多种解决方案和多个目标

默认情况下，Gurobi 优化器假定您的目标是为具有单个目标函数的模型找到一个经过验证的最优解。Gurobi提供了允许您放宽这些假设的功能。有关如何请求多个解决方案的信息，请参阅解决方案池部分;有关如何指定多个目标函数并控制它们之间的权衡的信息，请参阅“多个目标”部分。