递归 

1.递归应该一种比较常见的实现一些特殊代码逻辑时需要做的，但常常也是最绕的一种方式，在解释递归 之前，我们用循环和递归来做个比较

         1.1.如果你打开一扇门后，同样发现前方也有一扇们，紧接着你又打开下一扇门...直到打开最后一扇门出去， 或者一直没有碰到尽头 （死循环）——'这就是循环'

        1.2.如果你打开一扇门，紧接着你又用钥匙打开了这扇门，然后你又看到一扇们...但是当你开到某扇门时， 发现前方是一堵墙无路可走了，你选择原路返回——'这就是递归'

2.通过上面的故事可以发现递归其实是两个过程

         2.1.'递'问题分解去的过程叫'递' -- 就像故事打开的门

         2.2.'归'遇到终止'递'的条件叫'归' -- 就像故事里的墙 

 满足递归的条件

1.递归是一种解决问题的方法，它从解决问题的各个小部分开始，直到解决最初的大问题。递
归通常涉及函数调用自身
2.还是上面开门的故事，你想知道你开启的第一个门，实际是距离墙的第几扇门，这个问题想要解决
根据第一条的概念进行拆分
    2.1.'分解成各个小部分'，也就是我要知道我下一扇门距离墙是第几扇门
    2.2.'这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样',我想知道开启第一扇门距离墙
    是第几扇门，和我想知道下一扇门距离墙的位置是第几扇门是一样的
    2.3.'存在递归终止条件',也就这些问题一层一层解析后，直到我知道扇的位置后终止，在一个个回来数

如何编写递归 

1.写出递推公式，找到终止条件
2.写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，
最后将递推公式和终止条件翻译成代码
3.编写递归代码的关键是，只要遇到递归，我们就把它抽象成一个递推公式，不用想一层层的调用关系，不要试图用人
脑去分解递归的每个步骤

递归到底是个什么

1.递归就是栈一种应用场景，也遵循着'先进后出的原则（后进先出）'

 递归阶乘

1.求5*4*3*2*1 的问题，用递归来解决三步走
    1.1.分解成各个小部分
         5 * fn(4)   参数n = 5-1
         5 * (4*fn(3))     参数n = 4-1
         5 * 4 * (3*fn(2))  参数n = 3-1
         5 * 4 * 3 * (2*fn(1)) 参数n =2-1
    1.2.推到成递归公式 fn(n) = n*fn(n-1) ,且fn(1) = 1
    1.3.终止条件 fn(1) = 1


// 代码
1.递归是栈的结构表现，所以它'递'的过程是在做压栈，'归'的过程在做出栈，其实本质，先算的是
终止条件，然后在依次向上传递
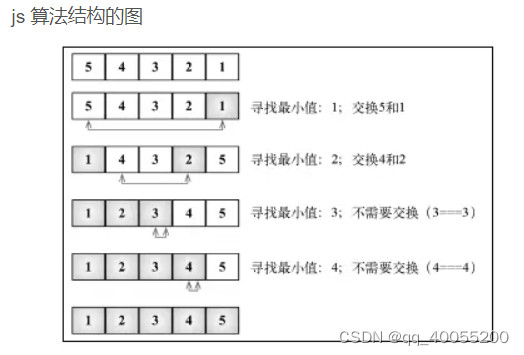
2.如图一，通过浏览器的控制台可以更形象的看出这个过程

function factorial(n){
    console.trace()
    if(n === 1 || n === 0){
        return 1
    }
    console.log(n)
    return n * factorial(n-1)
}
factorial(5)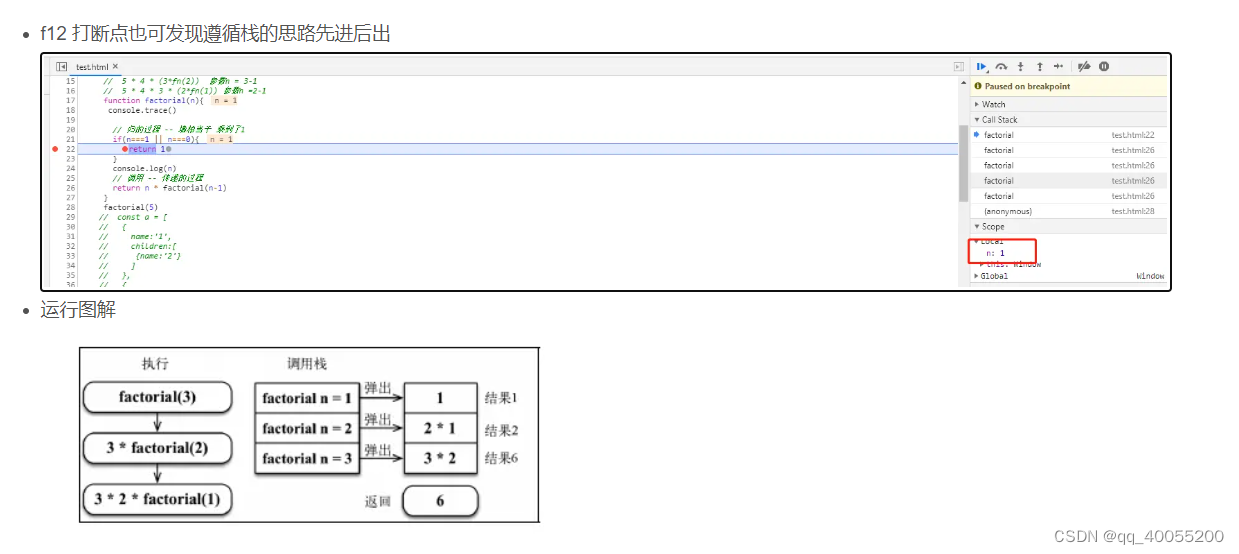

 斐波那契数列

0，1，1，2，3，5，8，13，21
// 斐波那契数列
function fibonacciIterative(n){
  if(n < 1) return 0  // 结束条件
  if(n <=2) return 1 // 结束条件
  return fibonacciIterative(n-2) + fibonacciIterative(n-1) // 递归公式 fn(n) = fn(n-1)+fn(n-2)
}


这段代码是一个使用递归方式求解斐波那契数列的函数。该函数接收一个整数参数 n，表示要求解的斐波那契数列的第 n 项（n 从 1 开始计数）。

首先判断 n 是否小于 1，如果是，则返回 0；如果 n 小于等于 2，返回 1，这两个条件是递归的结束条件。

如果 n 大于 2，则通过递归公式 fn(n) = fn(n-1)+fn(n-2) 计算第 n 项的值，即该项的前两项之和，继续调用 fibonacciIterative 函数求解第 n-1 和 n-2 项的值。

递归函数会不断地向下调用自身，直到满足结束条件才返回结果值。由于递归函数会反复调用自身，并且存在重复计算，因此在计算较大的斐波那契数列时，可能会出现性能问题。



// 优化的代码
1.向求解斐波那契数列时候，将求解过程图形化，可以看出，有些已经
求过的结点我们还会反复在求，如果把这些一求过的数存起来直接用，也会
提高效率

function fibonacciMemoization(n){
    const memo = [0,1]
    const fibonacci = (n) => {
        if(meno[0] != null) return memo[n]
        return memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo);
    }
     return fibonacci(n);
}

树 

二叉树搜索树 （快速查找）二叉树查找法

1.首先左侧节点存储（比父节点）小的值，右侧节点存储（比父节点）大的值，也就当我们每次去查的时候，
只要去比较查询节点和当前比较父节点大小，来决定他是走左面查询，还是右面查询，这样就不用去遍历
整个树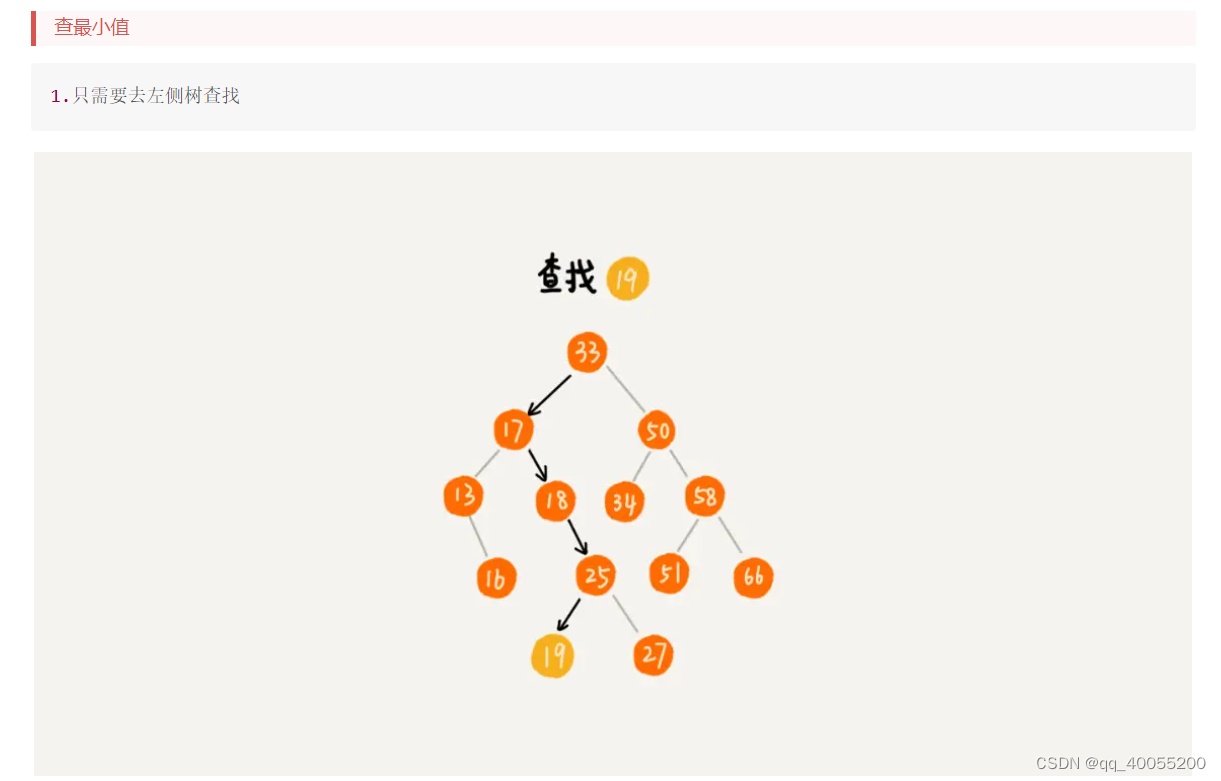

插入 

1.插入后的数据一定要符合左侧节点存储（比父节点）小的值，右侧节点存储（比父节点）大的值，因此插入的时候也是要先和根节点比较，直到找到末尾，来决定插入的值是作为叶节点左侧还是右侧

插入重复数据解决
1.二叉查找树中每一个节点不仅会存储一个数据，因此我们通过链表和支持动态扩容的数组等数据结构，把值相同的数据存储在同一个节点上
2.每个节点仍然只存储一个数据。在查找插入位置过程中，如果碰到一个节点的值，与要插入数据的值相同，就将这个要插入的数据放到这个节点的右子树，也就是说，把这个新插入的数据当作大于这个节点的值来处理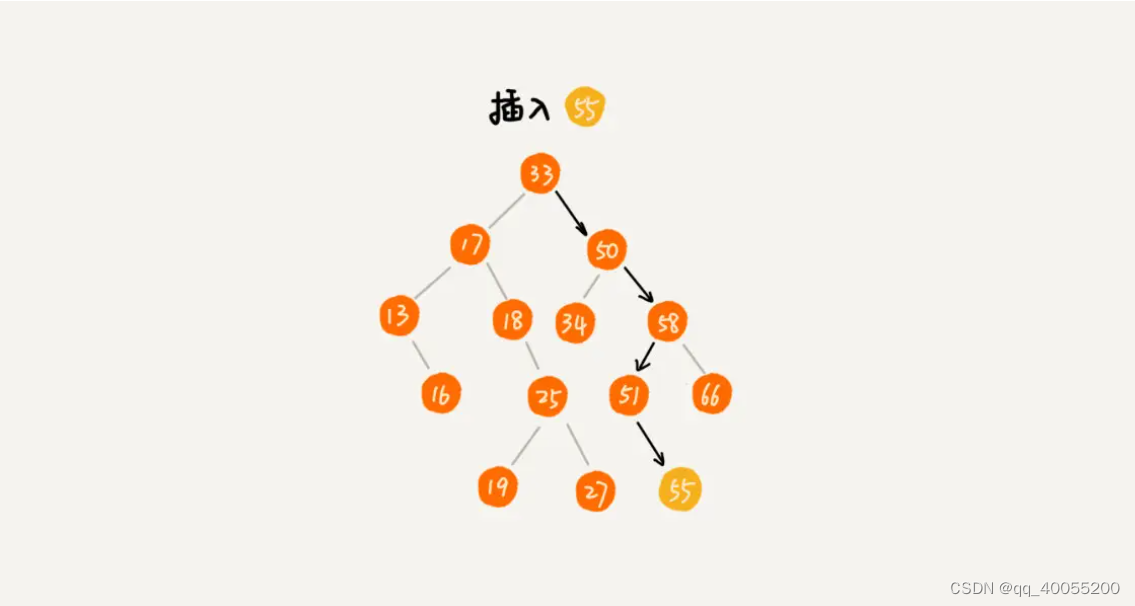

 排序

选择排序 

思路：

1.找到数据中最小值并将放到第一位，然后找到第二小的将其放到第二位

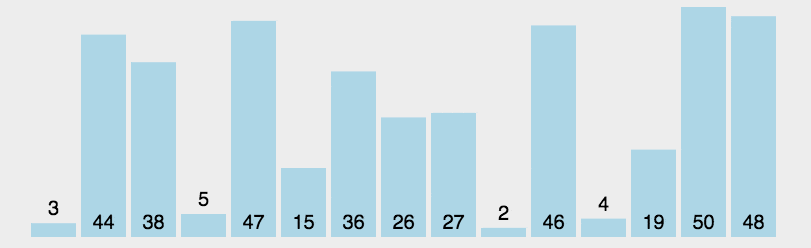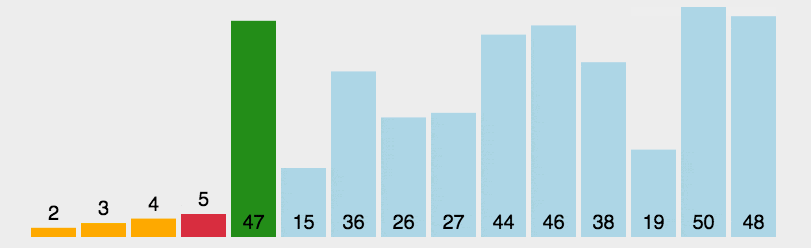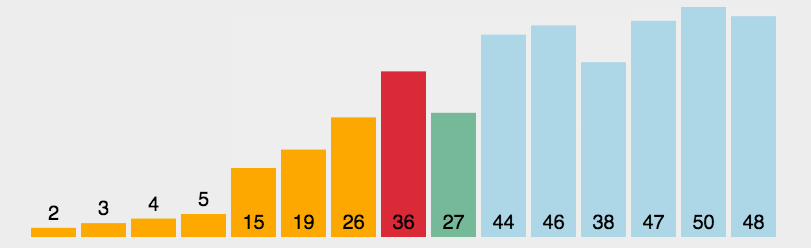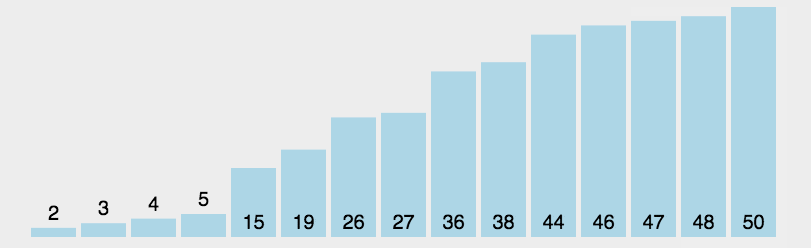
2.选择排序分成两个区间，分别是“排序区间”和“未排序区间”，选择排序每次会从“未排序区间”中找到最小元素，将其放到末尾

3.对引用图说明一下，引用第一个图中的第二个数据说明

        ‘1 5 6 3 2 4’,现在的1是排序区间，‘5 6 3 2 4’是为了排序区间，说明图虽然是5和2直接交换，但实际末尾的'4'也是比较过了的，只是图上没参与本次运算

1.这里有个思维转换，当我们求一个数组中最小值和最大值的时候，我们用等价替换的方法，只是 循环了一次，
问题来了当我们要把数组中所有的都进行排序那单单的一次循环肯定不够的，这时候就是双层for 循环
2.这里还要注意的是'选择排序'的概念，我们其实会将整个数组分成两个区域，'排序区间'和'未排序区间'，其中'排序区间'
是在数组前半部分，因此已经排序过的地方肯定是不需要在进行排序因此第二层的循环条件也变成了'let j = i; j < length; j++'

    
  // 选择排序
  function selectionSort(array, compareFn = defaultCompare) {
    const {
      length
    } = array
    let indexMin
    for (let i = 0; i < length-1; i++) {
      // 等价替换
      indexMin = i
      for (let j = i; j < length; j++) {
        if (compareFn(array[indexMin], array[j]) === Compare.BIGGER_THAN) {
          indexMin = j
        }
      }
      if (i !== indexMin) {
        swap(array, i, indexMin)
      }
    }
    return array
  }

  console.log(selectionSort(array))

插入排序

1.插入排序每次排一个数组项，以此方式构建最后的排序数组。假定第一项已经排序了，接着，它和第二项进行比较第二项是应该待在原位还是插入到第一项之前呢？这样，头两项就正确排序，接着和第三项比较，以此类推
2.通俗的理解'插入排序'和'选择排序' 在整体思路方面差不多，首先'插入排序'也是将整个排序分成两个区间，分别是'排序区间'和'未排序区间',每次会从'未排序区间'中取值去以排序区间中比较，比较后将这个值插入到'以排序区间'
3.'插入排序'和'选择排序'  做个比较理解，'插入'是从'未排序区间'取值在'以排序区间去比较'，'选择'是从'未排序区间'
依次找到最小值放到'以排序区间'
4.如图红色区域就是'已排序区间'，黄色就是'未排序'区间，依次从黄色区域取值去红色区域比较，并且将值插入到合适的红色区域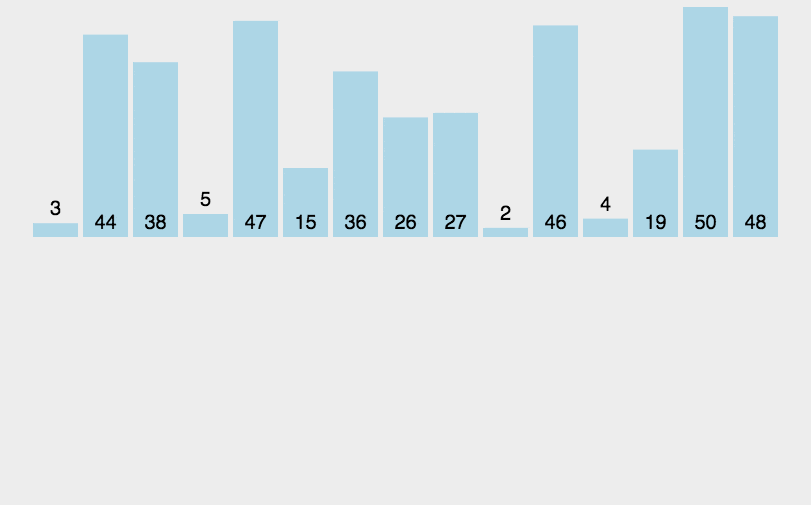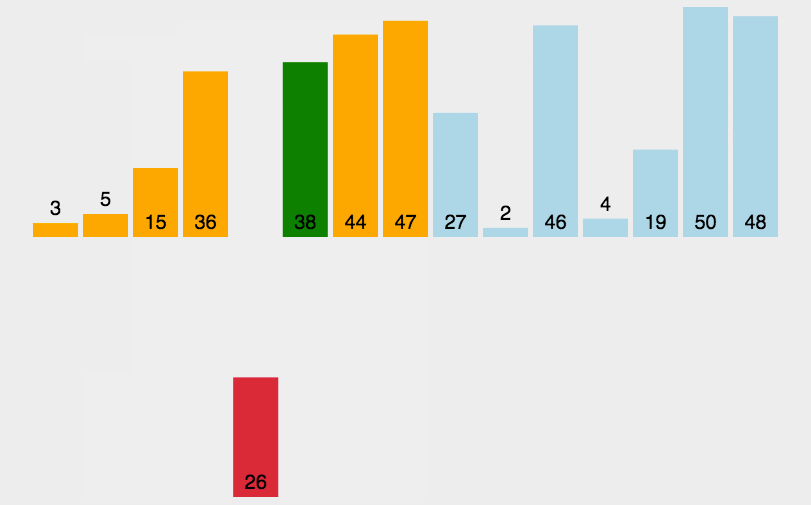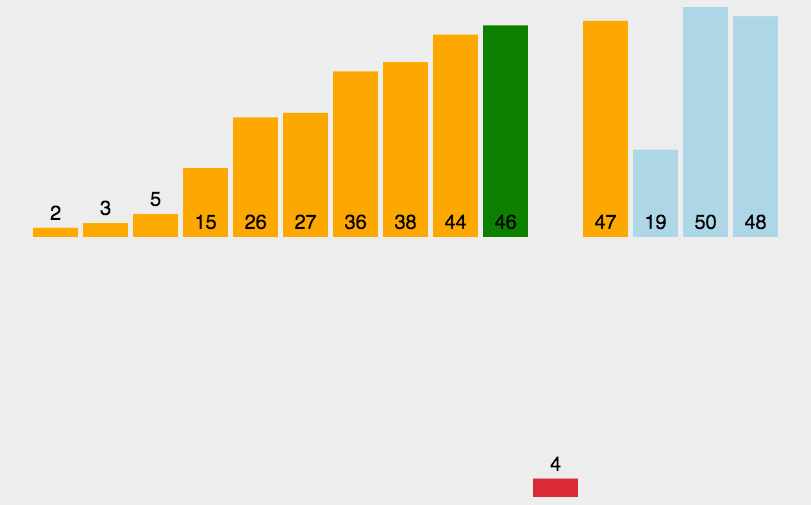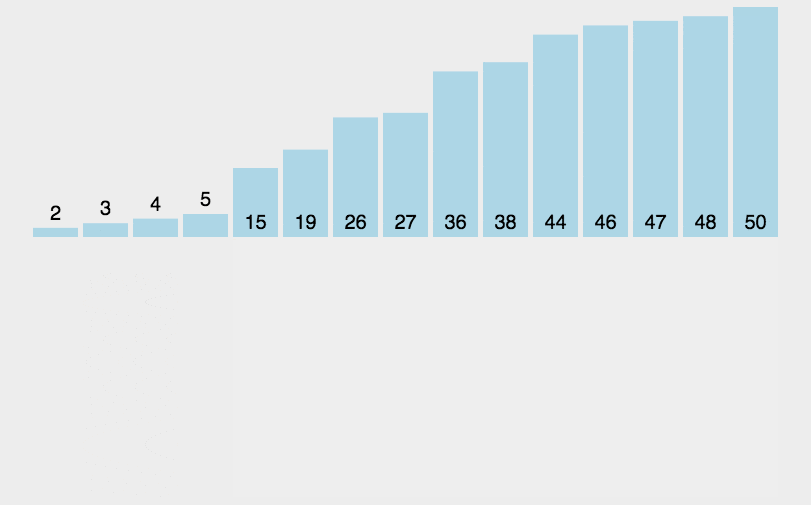

 

1.这里默认将第一个元素作为'已排序'区间中的内容，这样方便后续逻辑
2.通过过动态图来理解下面插入算法中的while逻辑，首先是吧整个数组分成两个区域
'已排序区域' 一个是 '为排序区域'，第一层for是从为排序区域取出一个，'已排序区域'就是
从当前这个值往后都是以排序区域，因此while 的判断循环j 是从取点位置开始的，注意
动图插入的那个动作，如果你比我小我就把你往后移动，如果你比我大我就到大了位置，
整个while 就结束了，这个值就到了j的位置

// 插入排序
  function insertionSort(array, compareFn = defaultCompare) {
    const {
      length
    } = array;
    let temp;
    for (let i = 1; i < length; i++) {
      let j = i;
      temp = array[i];
      while (j > 0 && compareFn(array[j - 1], temp) ===
        Compare.BIGGER_THAN) {
        array[j] = array[j - 1];
        j--;
      }
      array[j] = temp;
    }
    return array;
  };
  insertionSort(array)
  console.log(array)

结构 -- 数组 · js数据结构与算法 · 看云