数学实验第三版（主编：李继成 赵小艳）课后练习答案（十四）（1）

news2025/11/4 9:10:53

实验十四：水塔水流量估计模型

练习一

1.海水温度随着深度的变化而变化,海面温度较高,随着深度的增加,海水温度越来越低.通过验观测得一组海水温度t与深度h的数据如下:

h/m

0

1.5

2.5

4.6

8.2

12.5

16.5

26.5

t/℃

23.5

22.9

20.1

19.1

15.4

11.5

9.5

8.2

要求:

(1)分别用多种数据插值方法找出温度t与深度h之间的近似函数关系;

(2)找出温度变化最快的深度位置,通过查询相关资料,了解这个特殊位置的实际应用价值.

(1)

clc;clear;
format long
h=[0,1.5,2.5,4.6,8.2,12.5,16.5,26.5];
t=[23.5,22.9,20.1,19.1,15.4,11.5,9.5,8.2];
x=0:0.1:26.5;
%拉格朗日插值
y=lglrcz(h,t,x);
figure(1)
plot(h,t,'.',x,y);
x0=ones(length(h),1);xx=[x0];
for i=1:length(t)-1
    x0=x0.*h';
    xx=[xx,x0];
end
p=inv(xx)*t'%多项式系数（从低到高排列）
%三次样条插值
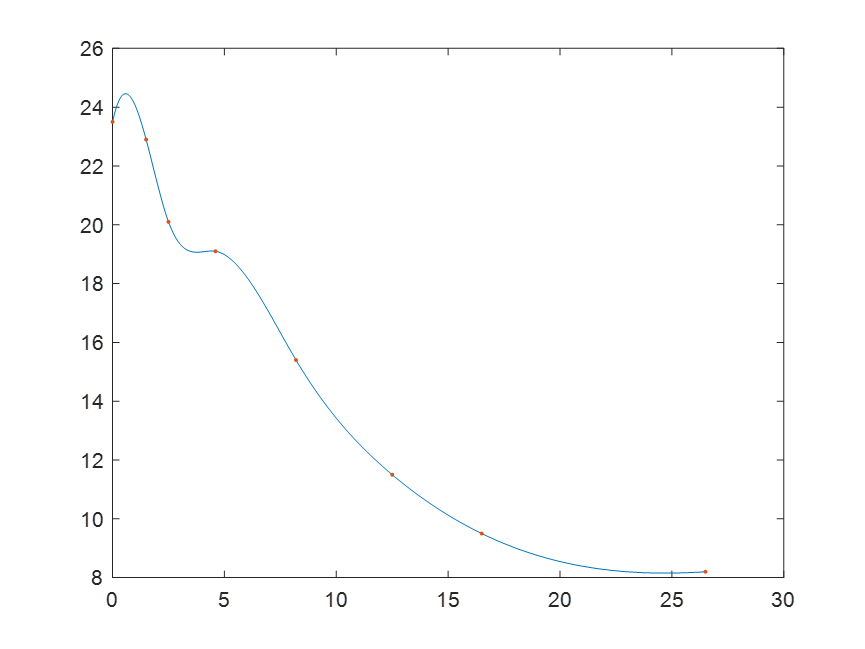
yy=interp1(h,t,x,'spline');
figure(2)
plot(x,yy,h,t,'.');
pp=spline(h,t)
function y=lglrcz(x0,y0,x)
n=length(x0);
m=length(x);
for i=1:m
    z=x(i);
    s=0.0;
    for k=1:n
        p=1.0;
        for j=1:n
            if j~=k
                p=p*(z-x0(j))/(x0(k)-x0(j));
            end
        end
        s=p*y0(k)+s;
    end
    y(i)=s;
end
end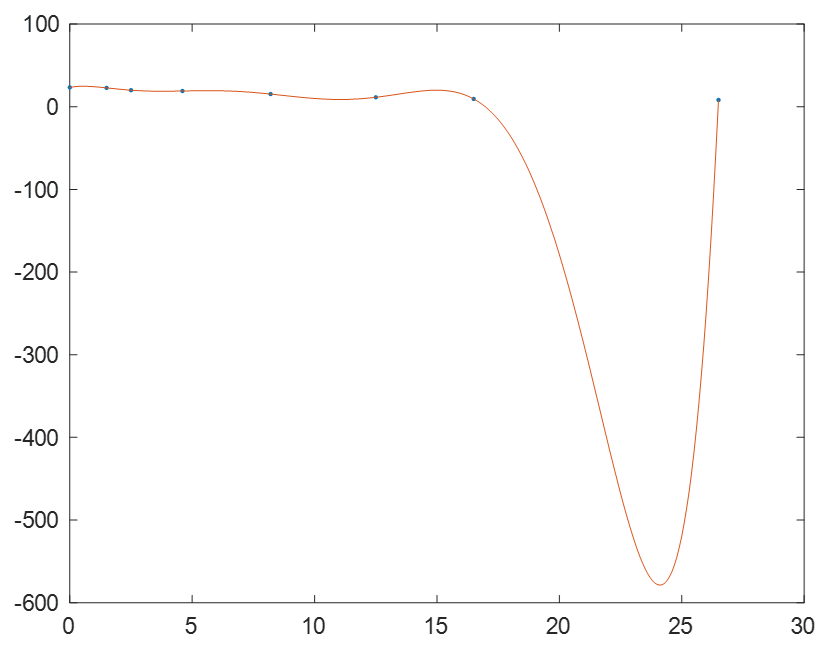

p =

  23.500000000000000

   5.519770260409278

  -6.784280947302284

   2.409485615066580

  -0.388966596330604

   0.030972950891118

  -0.001174710590966

   0.000016740427015

pp =

  包含以下字段的 struct:

      form: 'pp'

    breaks: [0 1.500000000000000 … ]

     coefs: [7×4 double]

    pieces: 7

     order: 4

       dim: 1

>> pp.coefs%三次样条插值的各区间的系数如下

ans =

   0.666350830669392  -3.625403322677568   3.538815615010219  23.500000000000000

   0.666350830669392  -0.626824584665302  -2.839526246004088  22.899999999999999

  -0.286563754712924   1.372227907342874  -2.094122923326514  20.100000000000001

   0.050422214507364  -0.433123747348549  -0.122004187338434  19.100000000000001

  -0.005736766041512   0.111436169330978  -1.280079468201690  15.400000000000000

  -0.000611295331494   0.037431887395469  -0.639946824277967  11.500000000000000

  -0.000611295331494   0.030096343417537  -0.369833901025942   9.500000000000000

（2）通过观察图像得知，变化最快的点应该在[0,8.2]内。

由于拉格朗日插值的龙格现象，我们不妨把x缩小范围，在小范围内求解。

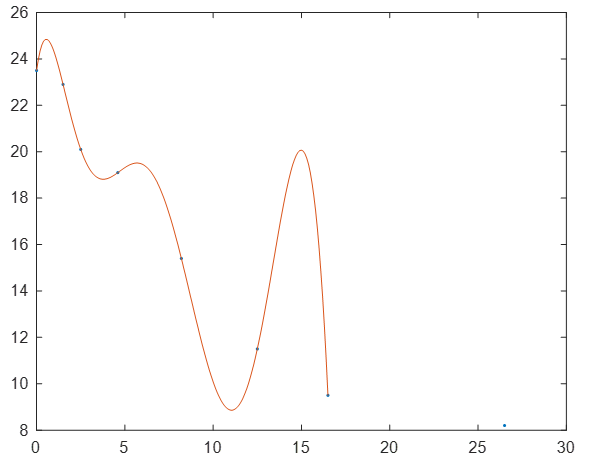
x1=0:0.1:16.5;%由于龙格现象，我们把x缩小范围进行求解
%拉格朗日插值
y=lglrcz(h,t,x1);
figure(1)
plot(h,t,'.',x1,y);
x0=ones(length(h),1);xx=[x0];
for i=1:length(t)-1
    x0=x0.*h';
    xx=[xx,x0];
end
p=inv(xx)*t'%多项式系数（从低到高排列）
function y=lglrcz(x0,y0,x)
n=length(x0);
m=length(x);
for i=1:m
    z=x(i);
    s=0.0;
    for k=1:n
        p=1.0;
        for j=1:n
            if j~=k
                p=p*(z-x0(j))/(x0(k)-x0(j));
            end
        end
        s=p*y0(k)+s;
    end
    y(i)=s;
end
end


pd=polyder(p);
xl=abs(polyval(p,x1));
x1(find(xl==max(xl)))

ans =

   16.5000

感觉龙格现象的影响，拉格朗日插值不太适合此题。

对于三次样条插值，我们在前四个区间内求解。

syms t
f1=0.6664*(t)^3-3.6254*(t)^2 +3.5388*(t) + 23.5;
f2=0.6664*(t-1.5)^3 -0.6268*(t-1.5)^2  -2.8395*(t-1.5) + 22.9;
f3=-0.2866*(t-2.5)^3+1.3722*(t-2.5)^2 -2.0941*(t-2.5)+ 20.1;
f4=0.0504*(t-4.6)^3 -0.4331*(t-4.6)^2  -0.1220*(t-4.6)+ 19.1;
f11=matlabFunction(diff(f1));
f22=matlabFunction(diff(f2));
f33=matlabFunction(diff(f3));
f44=matlabFunction(diff(f4));
t1=0:0.1:1.5;t2=1.5:0.1:2.5;t3=2.5:0.1:4.6;t4=4.6:0.1:8.2;
f111=f11(t0)
f222=f22(t0);
f333=f33(t0);
f444=f44(t0);
max(abs(f111))
max(abs(f222))
max(abs(f333))
max(abs(f444))
%显然最大值在第一个区间内
t1(find(f111==3.5388))

ans =

    3.5388

 ans =

    3.0357

ans =

    2.0941

ans =

    1.3624

ans =

     0

这两种方法得到的结果差别很大，估计是由于选择的插值方法不是很合适，个人疑问：这个数据所给的为何会插值得到奇怪的曲线，刚开始为何深度变大而温度升高呢？

个人建议还是改成拟合较好。

温度变化快的地方可以用来海水温差发电，且发电效率更高。

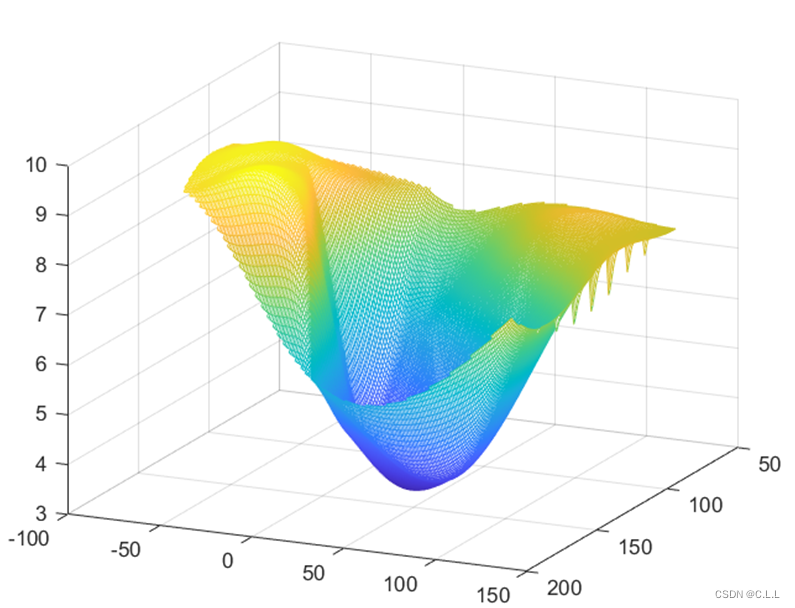
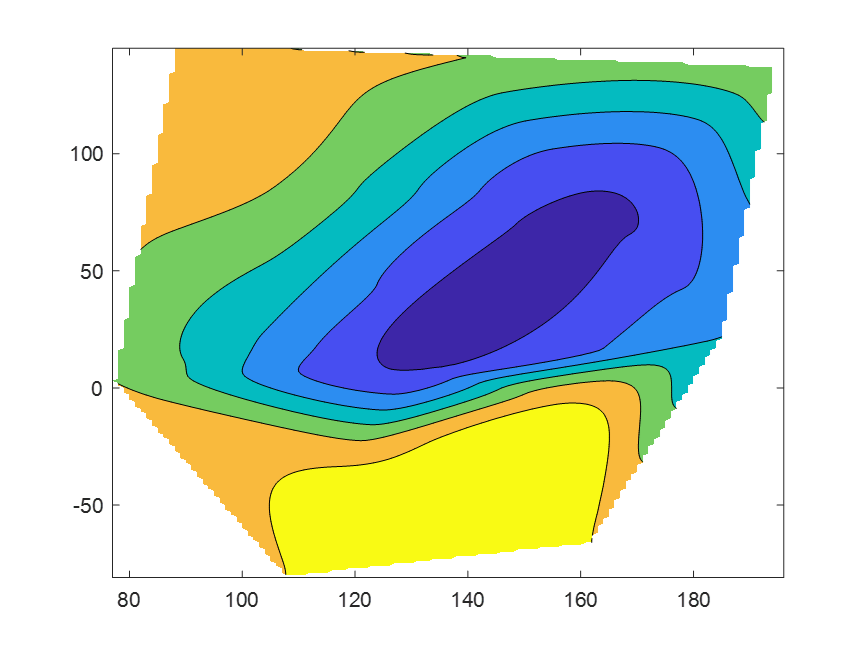
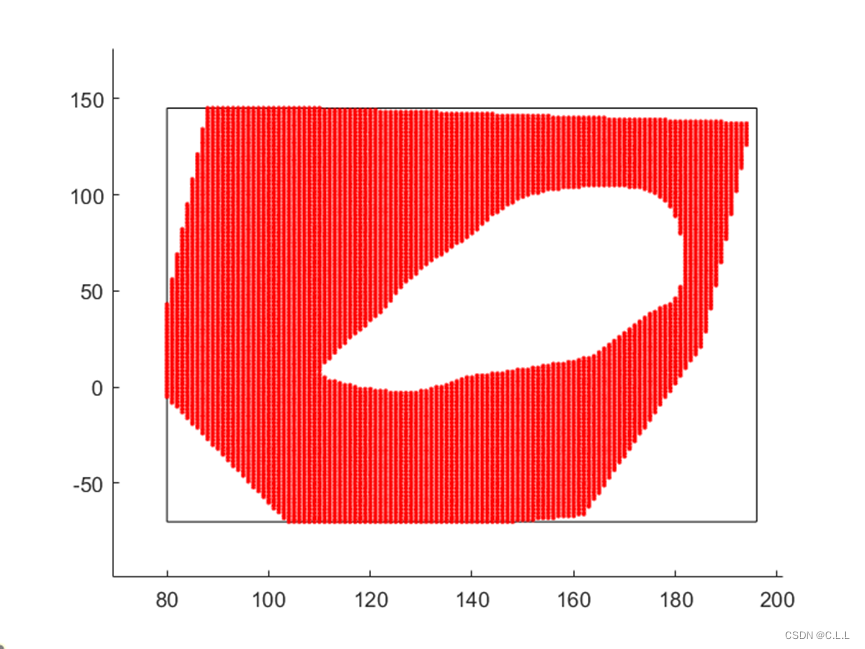
2.表14.8给出了在低潮时某一平面区域内若干点(x,y)处的水深z值(单位:ft).已知船的吃水深度为5ft.试画出海底的地貌图,并在平面矩形区域(80,196)x(-70,145)内标注哪些地方船要避免进人·

表14.8 水域坐标数据

x

129.0

140.5

103.5

88.0

185.5

195.0

105.5

157.5

107.5

77.0

81.0

162.0

162.0

117.5

y

7.5

141.5

23.0

147.0

22.5

137.5

85.5

-6.5

-81.0

3.0

56.5

-66.5

84.0

-33.5

z

4

8

6

8

6

8

8

9

9

8

8

9

4

9

clc;clear;
x=[129.0,140.5,103.5,88.0,185.5,195.0,105.5,157.5,107.5,77.0,81.0,162.0,162.0,117.5];
y=[7.5,141.5,23.0,147.0,22.5,137.5,85.5,-6.5,-81.0,3.0,56.5,-66.5,84.0,-33.5];
z=[4,8,6,8,6,8,8,9,9,8,8,9,4,9];
xx=77:196;
yy=-81:145;
[xxx,yyy]=meshgrid(xx,yy);
zzz=griddata(x,y,z,xxx,yyy,'cubic');
figure(1)
mesh(xxx,yyy,zzz);
figure(2)
contourf(xxx,yyy,zzz);%等高线
figure(3)
rectangle('Position',[80,-70,116,215]);%画矩形，[左下横，左下纵，长，宽]
for xi=80:196
    for yi=-70:145
        if zzz(find(yy==yi),find(xx==xi))>5
            hold on
            plot(xi,yi,'r.');
        end
    end
end

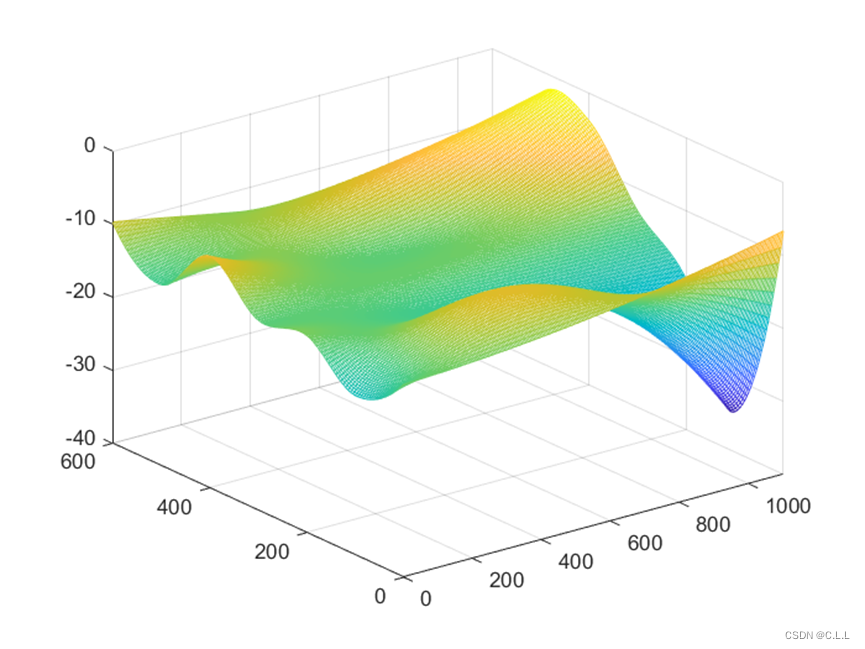
3.估计煤矿的储量.表14.9给出了某露天煤矿在平面矩形区域(1100mx700m)内,纵横均匀的网格交点处测得的煤层厚度(单位:m).由于客观原因,有些点无法测量煤层厚度,用‘—’标出,其中每一网格均为100mx100m的小矩形,试根据这些数据,用不同的方法估算该矩形区域煤矿的储藏量(体积)。

表14.9 煤层厚度

A

B

C

D

E

F

G

H

I

J

K

1

—

—

12.5

13.5

17.2

—

8.8

14.7

8.0

13.0

—

2

—

—

—

15.6

18.2

13

6.4

8.9

9.2

11.7

—

3

—

12

13.5

13.5

17.8

16.9

13.2

—

—

—

—

4

7.5

12.6

14.9

18.7

17.7

17.5

14.7

13

—

—

6.5

5

8.9

7.8

12.4

13.5

15.7

17.6

11.7

9.6

9.2

9.5

8.6

6

—

—

—

13.7

13.6

16.5

12.5

8.7

9.7

—

—

7

—

—

8.6

11.8

12.5

11.3

13.4

—

—

—

—

首先，我对该题有一个疑问：图中只给出了7*11个数据（姑且将‘—’也称为数据），每个数据是网格交点处的煤层厚度，而题中又说该平面区域为1100mx700m，可是表中的数据怎么画出1100mx700m的区域呢（十一个点只有十个线段啊），那该怎么办呢？

姑且每行都拟合让其拥有7*12个数据，把平面区域改为1100mx600m，这样才能有效地估计煤矿的仓储量。

clc;clear;
format long
x=0:100:1100;
y=0:100:600;
z=xlsread("C:\Users\dell\Desktop\煤层厚度.xlsx");
zz=[];
for i=1:7
    l=length(find(isnan(z(i,:))==0));
    ll=find(isnan(z(i,:))==0);
    lll=z(i,:);
  p=polyfit(1:l,lll(ll),2);
  m=polyval(p,1:12);
  if length(find(m<0))>0
      p=polyfit(1:l,lll(ll),1);
      m=polyval(p,1:12);
  end      
  zz=[zz;m];
end
[x,y]=meshgrid(x,y);
x0=0:5:1100;
y0=0:5:600;
[xx0,yy0]=meshgrid(x0,y0);
zz0=interp2(x,y,zz,xx0,yy0,'cubic');
mesh(xx0,yy0,-zz0);
v=0;
for k=1:length(x0)-1
    for i=1:length(y0)-1
        h=(zz0(i,k)+zz0(i+1,k)+zz0(i,k+1)+zz0(i+1,k+1))/4;
        v=v+25*h;
    end
end
v

v =

     8.597807745430814e+06

本文由作者自创，由于时间原因，难免出现些许错误，还请大家多多指正。创作不易，请大家多多支持。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1455711.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

阿里云服务器配置怎么选？CPU内存带宽配置多大？

阿里云服务器配置怎么选？CPU内存带宽配置多大？

阿里云服务器配置怎么选择&#xff1f;根据实际使用场景选择&#xff0c;个人搭建网站可选2核2G配置&#xff0c;访问量大的话可以选择2核4G配置&#xff0c;企业部署Java、Python等开发环境可以选择2核8G配置&#xff0c;企业数据库、Web应用或APP可以选择4核8G配置或4核16G配…
阅读更多...
IDEA2023.3.4开启SpringBoot项目的热部署【简单明了4步操作】

IDEA2023.3.4开启SpringBoot项目的热部署【简单明了4步操作】

添加devtools依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-devtools</artifactId><scope>runtime</scope><optional>true</optional> </dependency>IDEA开启自动编译 …
阅读更多...
Windows11(非WSL)安装Installing llama-cpp-python with GPU Support

Windows11(非WSL)安装Installing llama-cpp-python with GPU Support

直接安装&#xff0c;只支持CPU。想支持GPU&#xff0c;麻烦一些。 1. 安装CUDA Toolkit (NVIDIA CUDA Toolkit (available at https://developer.nvidia.com/cuda-downloads) 2. 安装如下物件&#xff1a; gitpythoncmakeVisual Studio Community (make sure you install t…
阅读更多...
对尾递归的理解（有哪些应用场景）

对尾递归的理解（有哪些应用场景）

文章目录 一、递归二、尾递归三、应用场景参考文献 一、递归 递归&#xff08;英语&#xff1a;Recursion&#xff09; 在数学与计算机科学中&#xff0c;是指在函数的定义中使用函数自身的方法 在函数内部&#xff0c;可以调用其他函数。如果一个函数在内部调用自身本身&am…
阅读更多...
如何将OSGB格式的倾斜模型转换成3DTiles？

如何将OSGB格式的倾斜模型转换成3DTiles？

通过以下方法可以将OSGB转换成3DTiles。 方法/步骤 1、下载三维地图浏览器 http://www.geosaas.com/download/map3dbrowser.exe&#xff0c;安装完成后桌面上出现”三维地图浏览器“图标。 2、双击桌面图标打开”三维地图浏览器“ 3、点击“倾斜模型”下拉菜单&#xff0c;…
阅读更多...
C++职工管理系统

C++职工管理系统

->需求分析以及案例展示、创建项目、创建职工管理类、菜单功能实现、退出系统功能实现、职工抽象类和普通员工类实现、经理类和老板类实现、添加职工功能实现、文件交互(->写文件、读文件1-文件未创建、读文件2-文件为空、读文件3-统计人数、读文件4-初始化完毕&#xff…
阅读更多...
代码提交commit规范工具

代码提交commit规范工具

一、idea工具 1.1安装 下载插件&#xff0c;以下是插件名 git commit message helper 安装后重启idea。 1.2使用 第一步&#xff1a; 根据代码提交的不同情况&#xff0c;选择不同的类型 feat表示&#xff1a;新增特性 fix表示&#xff1a;修复bug 等等。。。。 1.3效果…
阅读更多...
扶贫助农|基于springboot的扶贫助农系统设计与实现(源码+数据库+文档)

扶贫助农|基于springboot的扶贫助农系统设计与实现(源码+数据库+文档)

扶贫助农系统目录 目录 基于springboot的扶贫助农系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、用户信息管理 2、扶贫任务管理 3、论坛信息管理 4、扶贫公告管理 四、数据库设计 1、实体ER图 五、核心代码 六、论文参考 七、最新计算机毕设选题推荐…
阅读更多...
2.18总结

2.18总结

这两天在加强对最短路径的学习&#xff0c;除了Floyed比较简单之外&#xff0c;dijkstra、bell-mandford和SPFA学起来感觉有些难&#xff0c;洛谷上的模板题卡了半天都没写出来&#xff0c;最后只能通过看题解来帮助自己完成。 SPFA 算法实现&#xff1a; 最短路径算法对比比较…
阅读更多...
java的泛型【详解】

java的泛型【详解】

定义类、接口、方法时&#xff0c;同时声明了一个或者多个类型变量&#xff08;如&#xff1a;<E>&#xff09; &#xff0c;称为泛型类、泛型接口&#xff0c;泛型方法、它们统称为泛型。 作用&#xff1a;泛型提供了在编译阶段约束所能操作的数据类型&#xff0c;并自…
阅读更多...
【MySQL】变量、流程控制

【MySQL】变量、流程控制

一、变量 在MySQL的存储过程与函数中&#xff0c;可以使用变量来存储查询或计算的中间结果数据&#xff0c;或者输出最终的结果数据。它可以分为用户自定义变量与系统变量 1、系统变量 1&#xff09;系统变量分为全局变量&#xff08;需要使用关键字global&#xff09;和会话…
阅读更多...
上位机图像处理和嵌入式模块部署（boost库的使用）

上位机图像处理和嵌入式模块部署（boost库的使用）

【 声明&#xff1a;版权所有&#xff0c;欢迎转载&#xff0c;请勿用于商业用途。 联系信箱&#xff1a;feixiaoxing 163.com】 作为c程序员来说&#xff0c;除了qt之外&#xff0c;另外值得学的开发库就是boost。boost本身包含的内容非常多&#xff0c;基本我们常用的功能都已…
阅读更多...
linux下ffmpeg调用GPU硬件解码（VDPAU/VAAPI）保存文件

linux下ffmpeg调用GPU硬件解码（VDPAU/VAAPI）保存文件

本文讲解在linux下面&#xff0c;如何通过ffmpeg调用GPU硬件解码&#xff0c;并保存解码完的yuv文件。 其实&#xff0c;ffmpeg自带的例子hw_decode.c这个文件&#xff0c;就已经能满足要求了&#xff0c;因此&#xff0c;本文就尝试讲解以下hw_decode这个例子。hw_decode.c可以…
阅读更多...
使用vscode传入参数的方式进行debug

使用vscode传入参数的方式进行debug

使用vscode传入参数的方式进行debug {// 使用 IntelliSense 了解相关属性。 // 悬停以查看现有属性的描述。// 欲了解更多信息&#xff0c;请访问: https://go.microsoft.com/fwlink/?linkid830387"version": "0.2.0","configurations": [{&quo…
阅读更多...
【AGI视频】Sora的奇幻之旅：未来影视创作的无限可能

【AGI视频】Sora的奇幻之旅：未来影视创作的无限可能

在五年后的未来&#xff0c;科技的发展为影视创作带来了翻天覆地的变化。其中&#xff0c;Sora视频生成软件成为了行业的翘楚&#xff0c;引领着全新的创作潮流。Sora基于先进的Transformer架构&#xff0c;将AI与人类的创造力完美结合&#xff0c;为观众带来了前所未有的视听盛…
阅读更多...
【分享】windows11 vmware centos7 搭建k8s完整实验

【分享】windows11 vmware centos7 搭建k8s完整实验

概述 开年第一天&#xff0c;补充下自己的技术栈。 参考文章: k8s安装 - 知乎 【Kubernetes部署篇】K8s图形化管理工具Dasboard部署及使用_k8s可视化管理工具-CSDN博客 centos7环境下安装k8s 1.18.0版本带dashboard界面全记录&#xff08;纯命令版&#xff09;_sysconfig1.…
阅读更多...
通俗易懂地解释OpenAI Sora视频生成的特点有哪些？与Runway Gen2、Pika有什么区别？缺点是什么？

通俗易懂地解释OpenAI Sora视频生成的特点有哪些？与Runway Gen2、Pika有什么区别？缺点是什么？

OpenAI的Sora模型是最近两天最火热的模型。它生成的视频无论是清晰度、连贯性和时间上都有非常好的结果。在Sora之前&#xff0c;业界已经有了很多视频生成工具和平台。但为什么Sora可以引起如此大的关注&#xff1f;Sora生成的视频与此前其它平台生成的视频到底有哪些区别&…
阅读更多...
MATLAB知识点：meshgrid函数（★★★★☆）返回二维网格坐标（在MATLAB中经常用于生成绘制三维图的数据）

MATLAB知识点：meshgrid函数（★★★★☆）返回二维网格坐标（在MATLAB中经常用于生成绘制三维图的数据）

讲解视频&#xff1a;可以在bilibili搜索《MATLAB教程新手入门篇——数学建模清风主讲》。​ MATLAB教程新手入门篇&#xff08;数学建模清风主讲&#xff0c;适合零基础同学观看&#xff09;_哔哩哔哩_bilibili 节选自第3章&#xff1a;课后习题讲解中拓展的函数 在讲解第三…
阅读更多...
入门级10寸加固行业平板—EM-I10J

入门级10寸加固行业平板—EM-I10J

亿道信息以其坚固耐用的智能终端设备而闻名&#xff0c;近日发布了一款理想入门级 10 英寸加固平板电脑—I10J。 EM-I10J​​ 这是一款 10 英寸的平板电脑&#xff0c;主要运行 Windows 10操作系统&#xff0c;带有硬化塑料外壳&#xff0c;具有 IP65 防水防尘功能和 MIL-STD 8…
阅读更多...
踩坑实录（Fourth Day）

踩坑实录（Fourth Day）

今天开工了&#xff0c;其实还沉浸在过年放假的喜悦中……今天在自己写 Vue3 的项目&#xff0c;虽说是跟着 B 站在敲&#xff0c;但是依旧是踩了一些个坑&#xff0c;就离谱……照着敲都能踩到坑&#xff0c;我也是醉了…… 此为第四篇&#xff08;2024 年 02 月 18 日&#x…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023