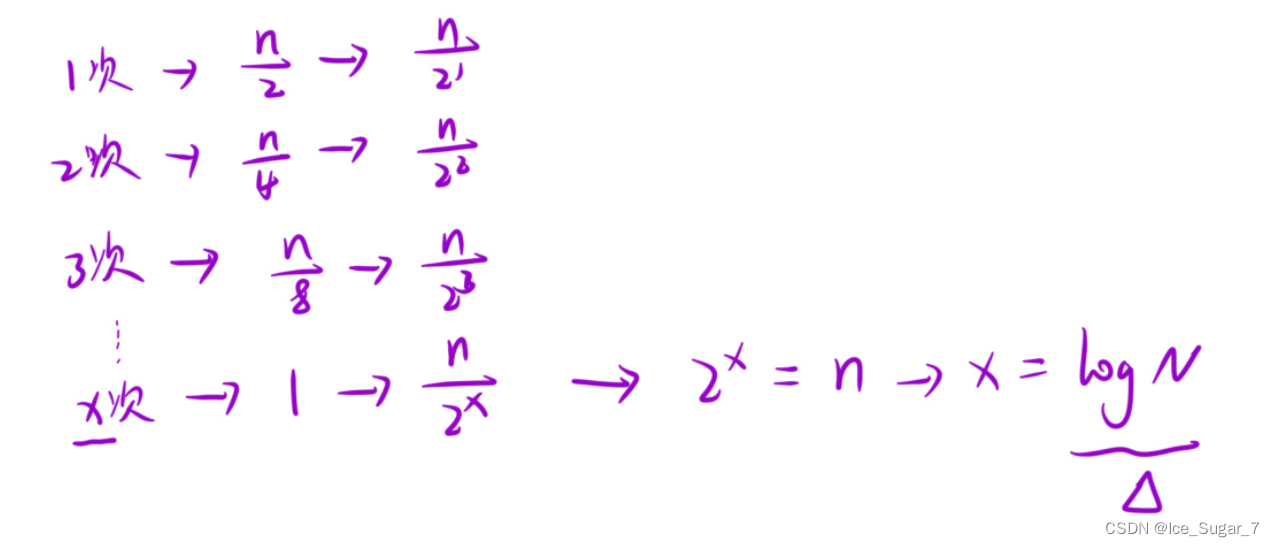概率基础——二项分布

news2025/8/17 13:09:00

概率基础——二项分布

介绍

在统计学中，二项分布是一种离散型概率分布，它描述了在一系列独立同分布的伯努利试验中成功的次数。这里我们以抛硬币为例，将一个硬币抛掷 $n$ 次，每次抛掷结果为正面向上的概率为 $p$ ，每次抛掷彼此之间都是相互独立的，随机变量 $X$ 对应的是 $n$ 次抛掷中正面向上的总次数。这种情况下，随机变量 $X$ 服从二项分布，参数为 $n$ 和 $p$ 。

理论及公式

二项分布的概率质量函数（PMF）为：

$\binom{n}{k} p^k (1-p)^{n-k}$

其中， $n$ 是试验次数， $p$ 是每次试验成功的概率， $k$ 是成功的次数。

示例与绘图

我们通过三组参数来绘制二项式分布的概率质量函数图：

1. $(n, p) = (10, 0.24)$
2. $(n, p) = (10, 0.5)$
3. $(n, p) = (10, 0.85)$

接下来，我们使用Python来实现绘制这些概率质量函数图。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom

# 参数设置
params = [(10, 0.24), (10, 0.5), (10, 0.85)]
colors = ['r', 'g', 'b']
labels = ['(10, 0.24)', '(10, 0.5)', '(10, 0.85)']

# 绘制概率质量函数图
plt.figure(figsize=(10, 6))
for i, (n, p) in enumerate(params):
    x = np.arange(0, n+1)
    pmf = binom.pmf(x, n, p)
    plt.plot(x, pmf, 'o-', color=colors[i], label=labels[i])

plt.title('Binomial Distribution PMF')
plt.xlabel('Number of Successes')
plt.ylabel('Probability')
plt.legend()
plt.grid(True)
plt.show()

PMF

运行以上代码，将会得到一个包含三个二项式分布概率质量函数图的图表。从图中可以看出，当成功概率 (p) 不同时，二项式分布的形态也会发生变化。当 (p) 接近 0.5 时，分布呈对称形态，而当 (p) 偏离 0.5 时，分布则呈现出偏斜的形态。

上述模拟采样实验可以得到每种试验结果所对应的次数，然后通过归一化，可以计算出随机变量每一种取值所对应的频数，并将其作为概率的近似进行绘图观测。
下面展示一些 内联代码片。

from scipy.stats import binom
import matplotlib.pyplot as plt

fig,ax = plt.subplots(3, 1)
params = [(10, 0.24), (10, 0.5), (10, 0.85)]
x = range(0, 11)
for i in range(len(params)):
    binom_rv = binom(params[i][0], params[i][1])
    rvs = binom_rv.rvs(size=10000)
    ax[i].hist(rvs, bins =10, density=True, alpha=0.75, edgecolor='black')
    ax[i].set_title('n = %i, p = %.2f' % (params[i][0], params[i][1]))
    ax[i].set_xlim(0, 10)
    ax[i].set_ylim(0, 0.6)
    ax[i].grid(ls="--")
    print(f'rvs {i}:%{rvs}')
plt.show()

采样示意图
程序打印的结果是3个数组，就是不同参数下分别做10万次采样试验的结果数组。
服从二项分布的随机变量的期望和方差公式如下：
$期望： E [X] = n p$
$方差： V [X] = n p (1 - p)$

import numpy as np
from scipy.stats import binom

binom_rv = binom(10, 0.24)
mean, var, skew, kurt = binom_rv.stats(moments='mvsk')
binom_rv = binom_rv.rvs(size=100000)
E_sim = np.mean(binom_rv)
S_sim = np.std(binom_rv, ddof=1)
V_sim = S_sim * S_sim

print('\nBinomial distribution simulation results')
print('  n = %i, p = %.2f' % (10, 0.24))
print(f'mean={mean},var={var}')
print(f'E_sim={E_sim},V_sim={V_sim}')
print(f'E=np={10 * 0.24}, V=np(1-p)={10 * 0.24 * 0.76}')