一、本周周赛总结

• 赛后半小时才做出T4 ，比赛时就没交
• T1 模拟。
• T3 贪心。
• T2/T4 Z函数/KMP。

100230. 修改矩阵

100230. 修改矩阵

1. 题目描述

2. 思路分析

• 转置要多想一会，可能还不如直接暴力写。

3. 代码实现

class Solution:
    def modifiedMatrix(self, g: List[List[int]]) -> List[List[int]]:              
        g = list(zip(*g))
        ans = [list(v) for v in g]
        for row,p in zip(g,ans):
            mx = max(row)
            for i,v in enumerate(row):
                if v == -1:
                    p[i] = mx         
                    
        return list(zip(*ans))

100219. 回文字符串的最大数量

100219. 回文字符串的最大数量

1. 题目描述

2. 思路分析

• 题目给出的任意次操作，也就是说可以把所有字符重排。那么回文题就可以先统计所有字符计数。
• 用奇数多出来那个字符优先放中间；偶数的放剩余位置。
• 实现时，只需记录奇偶的数量即可。
• 另外需要按字符串从短到长，优先排短的。
• 为了避免复杂的分类讨论，每个串计算需要几个奇数几个偶数（即使是偶数串）；如果奇数串不够，用偶数串补。

3. 代码实现

class Solution:
    def maxPalindromesAfterOperations(self, words: List[str]) -> int:
        cnt = Counter()
        ds = []
        for w in words:
            ds.append(len(w))
            for c in w:
                cnt[c] += 1
        one = two = 0
        for v in cnt.values():
            one += v % 2 
            two += v // 2
        ans = 0 
        for d in sorted(ds):
            need_one = d&1  # 需要补一个奇数
            d //= 2
            if need_one and not one and two:  # 没奇数用偶数补                 
                two -= 1
                one += 2
            if one >= need_one and two >= d:  # 奇偶都够
                one -= need_one
                two -= d
                ans += 1                   
          
        return ans 

100198. 匹配模式数组的子数组数目 II

100198. 匹配模式数组的子数组数目 II

1. 题目描述

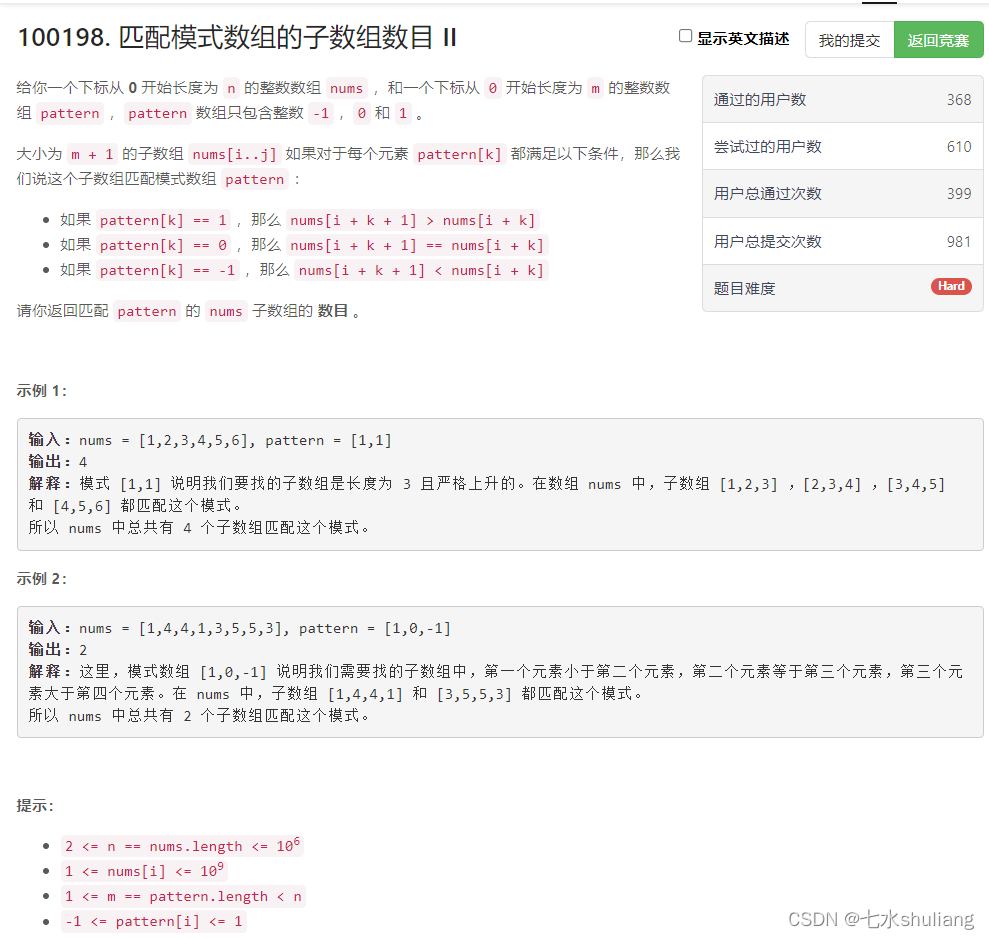
2. 思路分析

连续两周出Z函数可还行。

• 模式数组指向了nums的’间隔位置’，那么可以把nums直接转化成’间隔数组’，套z函数或者kmp即可。

---

• 注意，不要用-1，这是俩字符

3. 代码实现

class ZFunction:

    def __init__(self, s):
        n = len(s)
        self.z = z = [0] * n
        l, r = 0, 0
        for i in range(1, n):
            if i <= r and z[i - l] < r - i + 1:
                z[i] = z[i - l]
            else:
                z[i] = max(0, r - i + 1)
                while i + z[i] < n and s[z[i]] == s[i + z[i]]:
                    z[i] += 1
            if i + z[i] - 1 > r:
                l = i
                r = i + z[i] - 1
    @staticmethod
    def find_all_match_pos(s, t):
        """从s中找到所有t的位置"""
        s = t + '#' + s
        n = len(t)
        z = ZFunction(s).z
        ans = []
        for i in range(n + 1, len(s)):
            if z[i] == n:
                ans.append(i - n - 1)
        return ans

class Solution:
    def countMatchingSubarrays(self, nums: List[int], pattern: List[int]) -> int:
        s = ''.join(['a' if x < y else ('b' if x == y else 'c') for x,y in pairwise(nums)]     )
        t = ''.join(['a' if v == 1 else ('b' if v == 0 else 'c') for v in pattern]     )  
        return len(ZFunction.find_all_match_pos(s, t))        

参考链接