6.3 图的遍历
一、概念
-
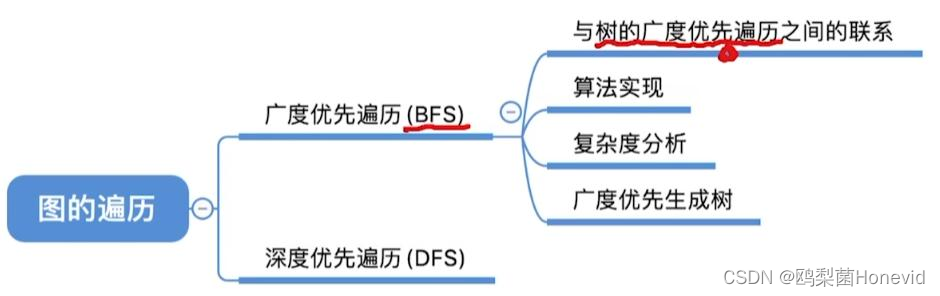
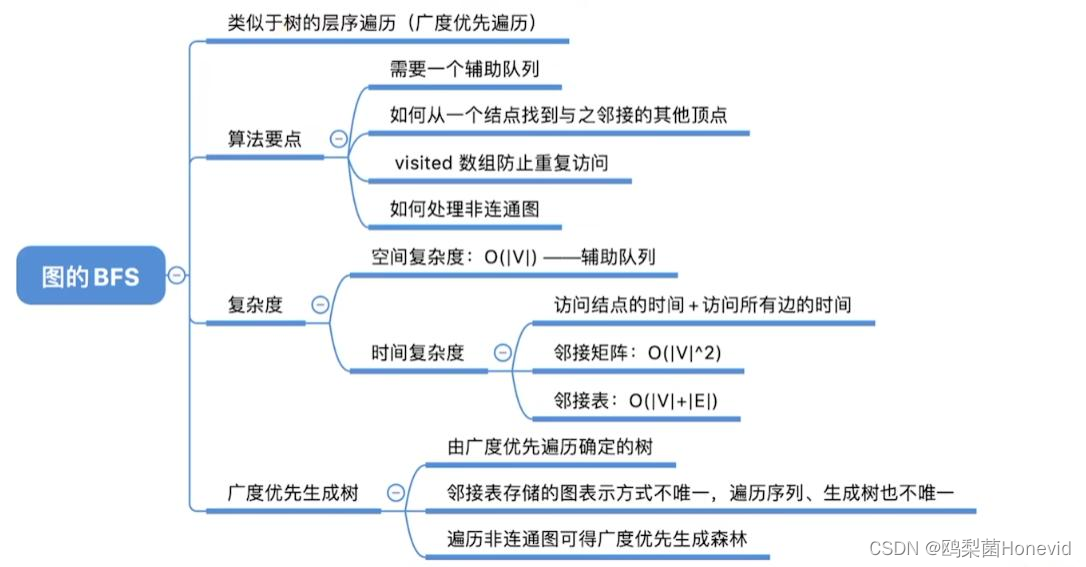
图的广度优先遍历
-
-
树的广度优先遍历(层序遍历):不存在“回路”,搜索相邻的结点时,不可能搜到已经访问过的结点:
-
若树非空,则根节点入队
-
若队列非空,队头元素出队并访问,同时将该元素的孩子依次入队
-
重复②直到队列为空
-
-
图的广度优先遍历(Breadth-First-Search,BFS):搜索相邻的顶点时,有可能搜到已经访问过的顶点
-
找到与一个顶点相邻的所有顶点
-
标记哪些顶点被访问过
-
需要一个辅助队列
-
-
上述图的广度优先遍历的缺陷:只能遍历连通图,非连通图无法遍历
-
改进的BFS算法:
-
遍历visited数组,如果该顶点未被访问,则调用BFS
-
BFS执行完成,回到①,直到所有顶点都被访问过
-
结论:对于无向图,调用BFS函数的次数=连通分量数
-
空间复杂度:最坏情况,辅助队列大小为 o(V)
-
-
广度优先遍历时间复杂度来源:找点、找边
-
邻接矩阵存储的图:
-
访问 V个顶点需要O(V)的时间
-
查找每个顶点的邻接点都需要O(V)的时间,而总共有V个顶点
-
时间复杂度=O(V²)
-
-
邻接表存储的图:
-
访问V个顶点需要O(V)的时间
-
查找各个顶点的邻接点共需要O(E)的时间
-
时间复杂度= O(V+E)
-
-
广度优先生成树
- 广度优先生成树由广度优先遍历过程确定。由于邻接表的表示方式不唯一,因此基于邻接表的广度优先生成树也不唯一。
-
广度优先生成森林
- 对非连通图的广度优先遍历,可得到广度优先生成森林
-
-
-
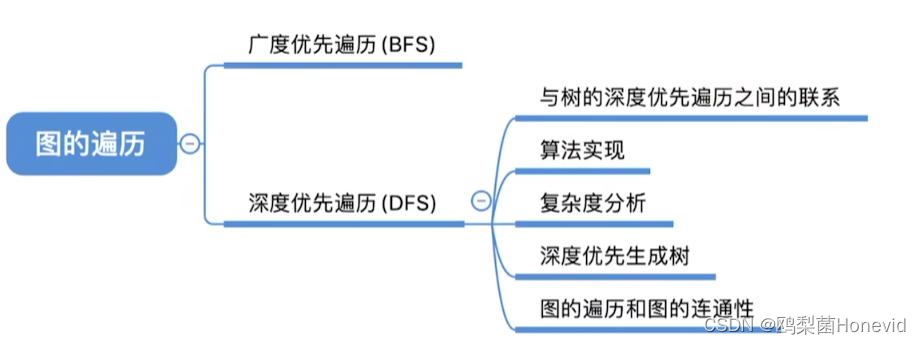
图的深度优先遍历DFS
-
-
树的深度优先遍历——其一:树的先根遍历:不存在重复访问问题
-
图的深度优先遍历:存在重复访问问题——设置标记数组:栈
-

-
上述DFS存在的问题:无法遍历非连通图
-
改进:与BFS改进相似
-
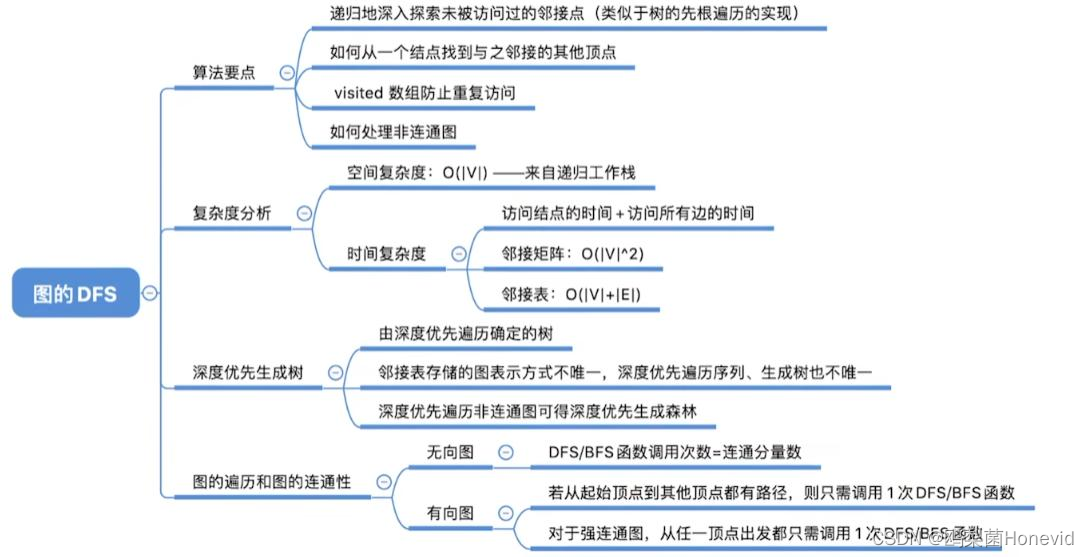
复杂度分析
-
空间复杂度:来自函数调用栈,最坏情况,递归深度为O(V)
-
时间复杂度=访问各结点所需时间+探索各条边所需时间
-
-
邻接矩阵存:时间复杂度:O(V²)
-
邻接表存:时间复杂度O(V+E)
-
-
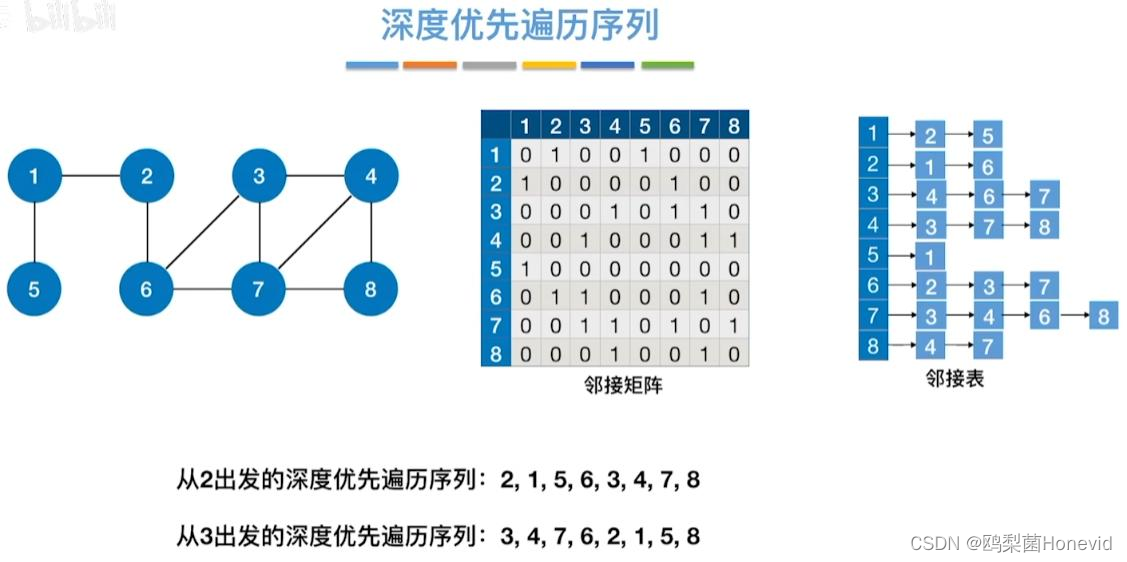
深度优先遍历序列唯一性与生成树个数
-
同一个图的邻接矩阵表示方式唯一,因此深度优先遍历序列唯一,深度优先生成树也唯一
-
同一个图邻接表表示方式不唯一,因此深度优先遍历序列不唯一,深度优先生成树也不唯一
-
-
-
图的遍历与图的连通性
-
对无向图进行BFS/DFS遍历
-
调用BFS/DFS函数的次数=连通分量数
-
对于连通图,只需调用1次 BFS/DFS
-
-
对有向图进行BFS/DFS遍历
-
调用BFS/DFS函数的次数要具体问题具体分析
-
若起始顶点到其他各顶点都有路径,则只需调用1次BFS/DFS 函数
-
对于强连通图,从任一结点出发都只需调用1次 BFS/DFS
-
-
-
二、理解
-
当各边的权值相等时,广度优先算法可以解决单源最短路径问题
-
图的广度优先遍历相当于树的层次遍历
-
广度优先遍历需要用到队列
-
深度优先遍历需要用到栈
-
图的深度优先遍历相当于树的先根遍历,广度优先相当于树的层次遍历
-
深度优先遍历可以判断图中是否存在环
-
使用DFS递归遍历无环有向图,在退出时递归输出相应的顶点,得到逆拓扑有序顶点序列
三、技巧
-
n个顶点,e条边的图采用邻接表存储,
-
BFS遍历时
-
时间复杂度:O(n+e):顶点表每个点和边表每个边都要遍历一次
-
空间复杂度:O(n):每个点都入一次队
-
-
DFS遍历时
-
时间复杂度:O(n+e):顶点表每个点和边表每个边都要遍历一次
-
空间复杂度:O(n):每个点都入一次队
-
-
-
画图的深度优先生成树、广度优先生成树:
-
先根据题目信息把图画出来
-
根据深度优先路径或广度优先路径,把不在路径上的边删去,即为生成树
-