1.题目

一共有 $n$ 个数，编号是 $1\sim n$，最开始每个数各自在一个集合中。

现在要进行 $m$ 个操作，操作共有两种：

1. M a b，将编号为 $a$ 和 $b$ 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
2. Q a b，询问编号为 $a$ 和 $b$ 的两个数是否在同一个集合中；

输入格式
第一行输入整数 n 和 m。

接下来 m行，每行包含一个操作指令，指令为 M a b 或 Q a b 中的一种。

输出格式
对于每个询问指令 Q a b，都要输出一个结果，如果 $a$ 和 $b$ 在同一集合内，则输出 Yes，否则输出 No。

每个结果占一行。

数据范围
$1\le n,m\le 10^5$

输入样例：

4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4

输出样例：

Yes
No
Yes

2.基本思想

1. 初始化

for(int i = 0; i < 8; i ++) p[i] = i;

上面的代码实现的结果如下图所示

很容易理解，就是将当前数据的父节点指向自己

2. 查找 + 路径压缩

int find(int x){ //返回x的祖先节点 + 路径压缩
    //祖先节点的父节点是自己本身
    if(p[x] != x){
        //将x的父亲置为x父亲的祖先节点,实现路径的压缩
        p[x] = find(p[x]);    
    }
    return p[x]; 
}

find的功能是用于查找祖先节点，那么路径压缩又是怎么完成的

注意图，当我们在查找1的父节点的过程中,路径压缩的实现

针对 x = 1

find(1) p[1] = 2  p[1] = find(2)
find(2) p[2] = 3  p[2] = find(3)
find(3) p[3] = 4  p[3] = find(4)
find(4) p[4] = 4  将p[4]返回

退到上一层
find(3) p[3] = 4  p[3] = 4 将p[3]返回
退到上一层
find(2) p[2] = 3  p[2] = 4 将p[2]返回
退到上一层
find(1) p[1] = 2  p[1] = 4 将p[1]返回

至此，我们发现所有的1，2，3的父节点全部置为了4，实现路径压缩；同时也实现了1的父节点的返回

合并操作
if(op[0] == ‘M’) p[find(a)] = find(b); //将a的祖先点的父节点置为b的祖先节点
假设有两个集合

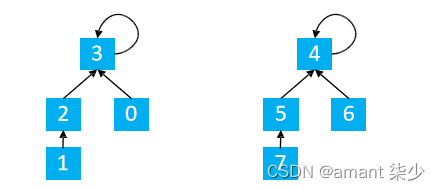
合并1， 5
find(1) = 3 find(5) = 4
p[find(1)] = find(5) –> p[3] = 4
如下图所示

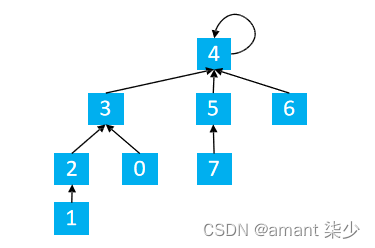
查找
find(a) == find(b)

总结
并查集

1. 将两个集合合并
2. 询问两个元素是否在一个集合中

基本原理：每个集合用一棵树来表示。树的编号就是整个集合的编号。每个节点存储它的父节点，p[x]表示x的父节点

1. 判断树根 if(p[x] = x)
2. 求x的集合编号 while(p[x] != x) x = p[x]
3. 合并两个集合，这两将x的根节点嫁接到y的根节点, px为x的根节点， py为y的根节点，嫁接p[px] = py

3.代码实现

import java.io.*;

public class _836合并集合 {
    static int N = 100010;
    static int[] p = new int[N];

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] s = br.readLine().split(" ");
        int n = Integer.parseInt(s[0]);
        for (int i = 0; i < n; i++) p[i] = i;//最开始 初始化
        int m = Integer.parseInt(s[1]);
        while (m-- > 0) {//m 次操作
            String[] s1 = br.readLine().split(" ");
            String opt = s1[0];
            int a = Integer.parseInt(s1[1]), b = Integer.parseInt(s1[2]);
            if (opt.equals("M")) p[find(a)] = find(b);
            else System.out.println(find(a) == find(b) ? "Yes" : "No");
        }
    }

    private static int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
}