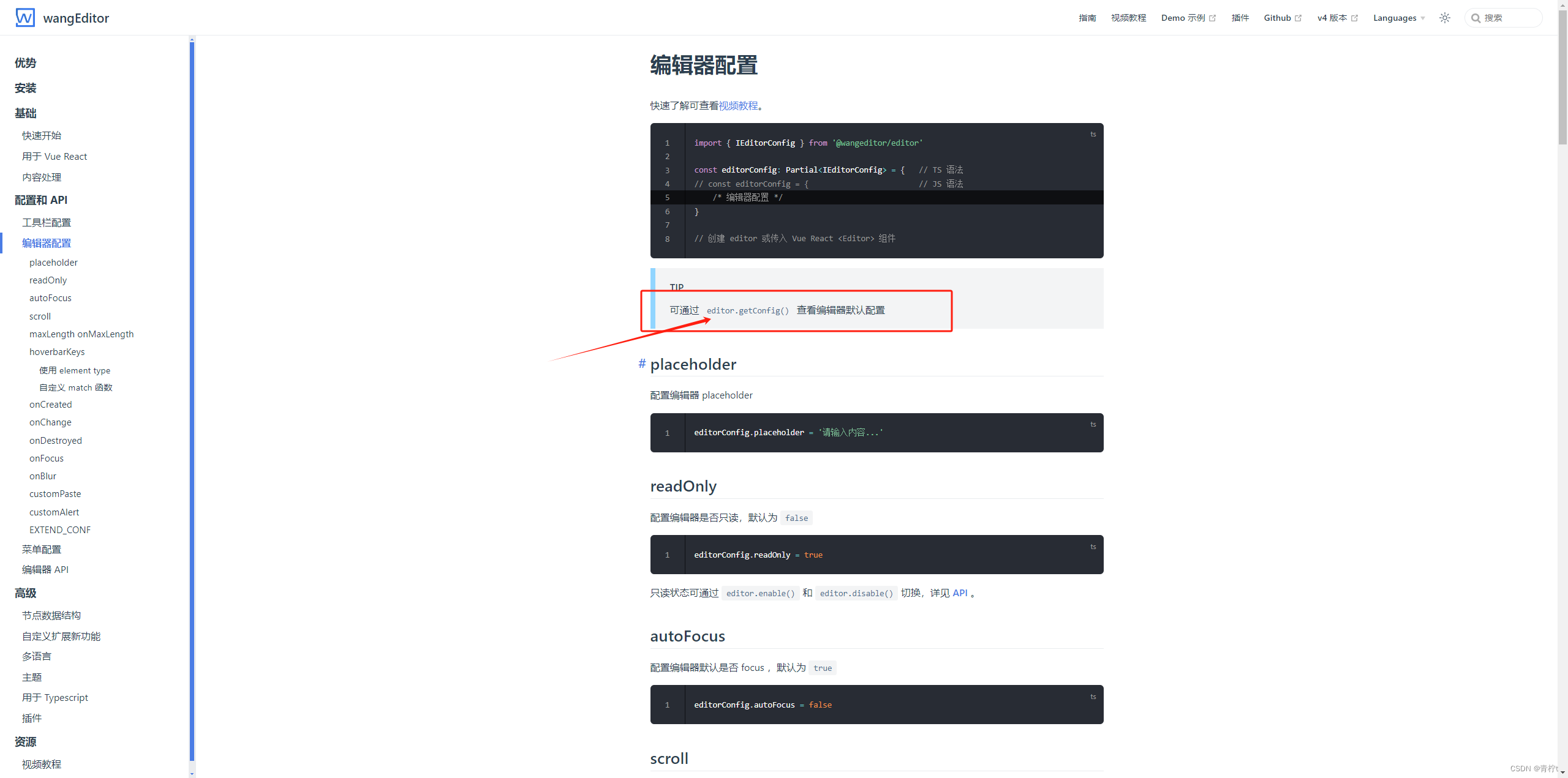
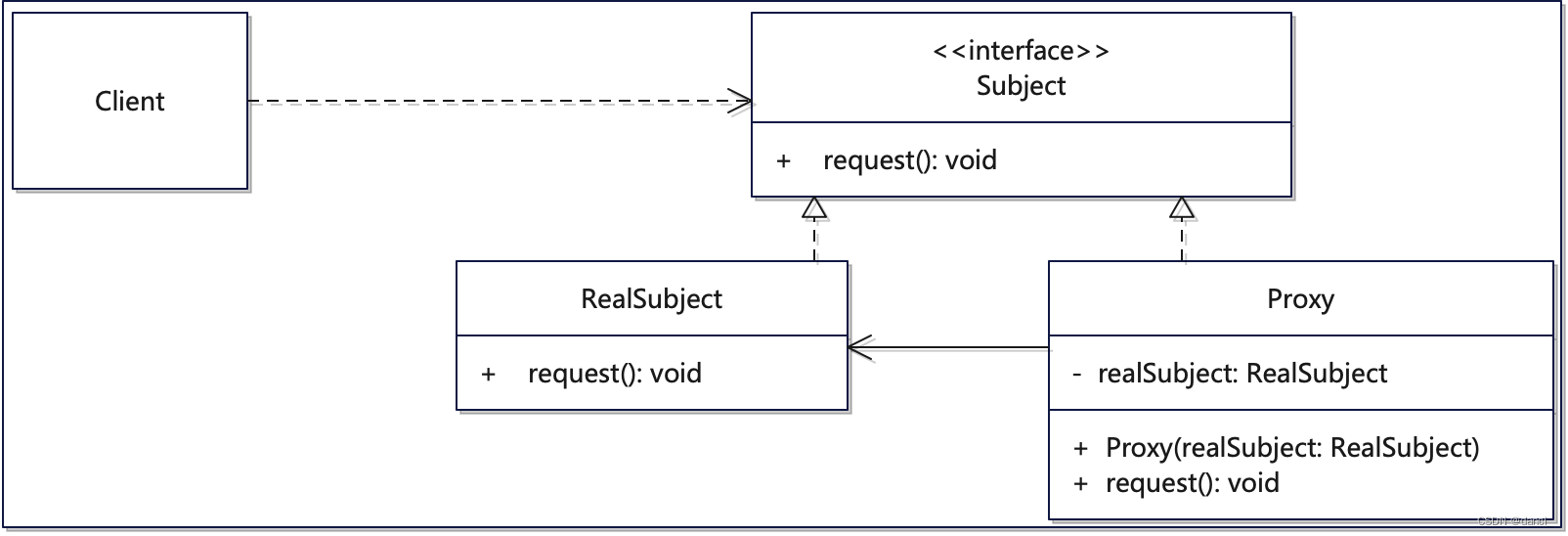
一阶导数
导数最大的作用是判断复杂函数的单调性,则可用一阶导判断原函数的单调性。
一阶导数>0:函数单调递增;
一阶导数<0:函数单调递减;
一阶导数=0:函数是常函数。
也可以通过一阶导数=0的根来判断出函数的单调区间,进而知道函数的趋势图像。而当一阶导数
无法判断函数的单调性时,需要二阶求导。
二阶导数
二阶导数可判断原函数的凹凸性。
二阶导数>0:一阶导数是单调增函数,即原函数在各店的切线斜率随x的增大而增大的,原函数是凹图像。
二阶导数<0:一阶导数是单调减函数,即原函数在各店的切线斜率随x的增大而减小的,原函数是凸图像。









![[Angular 基础] - 指令(directives)](https://img-blog.csdnimg.cn/direct/1801a18ad0fe4e7e9722b308055506e3.png)