回顾

图的Node数据结构

图的数据结构，以下两种都可以，dfs和bfs的板子是不变的。

class Node {
    public int val;
    public List<Node> neighbors;
    public Node() {
        val = 0;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val) {
        val = _val;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val, ArrayList<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}

```java
public class Node{
    public int value;//点的编号，不一定是Integer类型的，要看具体的题，有的题点编号为字母。
    public int in;//入度
    public int out;//出度
    public ArrayList<Node>nexts;//出去的边直接相连的邻居。
    public ArrayList<Edge>edges//出去的边

    public Node(int value){
        this.value=value;
        in = 0;
        out = 0;
        nexts = new ArrayList<>();
        edges = new ArrayList<>();
    }

}

bfs和dfs的板子

图和二叉树的宽搜最大的不同的就是，图是可能有环的。二叉树是没环的，所以图可能死循环卡住，所以需要额外记录是否有访问过，一般是哈希表或者数组。
深搜是点入栈之前就需要处理了，广搜是点入队列之后开始处理。

public static void bfs(Node node){
    if(node==null) return;
    Queue<Node> queue = new LinkedList<>();
    HashSet<Node> set = new HashSet<>();
    queue.add(node);
    set.add(node);
    while(!queue.isEmpty()){
        Node cur = queue.poll();
        /*  具体的处理逻辑
            （宽搜一般是结点入队列后再处理）
        */
        for(Node next: cur.nexts){
            if(!set.contains(next)){//如果set中没有，那么说明这个next结点没有被访问过
            queue.add(next);//扔到队列里
            set.add(next);//并且标记访问
            }
        }
    }
}

public static void dfs(Node node){
    if(node==null) return;
    Stack<Node> stack = new Stack<>();
    HashSet<Node> set = new HashSet<>();
    stack.add(node);
    set.add(node);
    /*具体的处理逻辑（深搜一般是结点入栈前就进行处理）*/
    while(!stack.isEmpty()){
        Node cur = stack.pop();
        for(Node next:cur.nexts){
            if(!set.contains(next)){
                stack.push(cur);//在这里需要把cur和next两个结点同时入栈是因为
                stack.push(next);//想在栈里保持深度搜索的路径。这次搜索相比于上一次搜索，在栈中就多了一个next结点。
                set.add(cur);
                set.add(next);
                /*具体的处理逻辑 */
                break;//之所以立马break是因为深搜每次只走一步，不像宽搜每次走一层。
            }
        }
    }
}

题目

给你无向 连通 图中一个节点的引用，请你返回该图的 深拷贝（克隆）。

图中的每个节点都包含它的值 val（int） 和其邻居的列表（list[Node]）。

class Node {
public int val;
public List neighbors;
}

测试用例格式：

简单起见，每个节点的值都和它的索引相同。例如，第一个节点值为 1（val = 1），第二个节点值为 2（val = 2），以此类推。该图在测试用例中使用邻接列表表示。

邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。

给定节点将始终是图中的第一个节点（值为 1）。你必须将 给定节点的拷贝 作为对克隆图的引用返回。

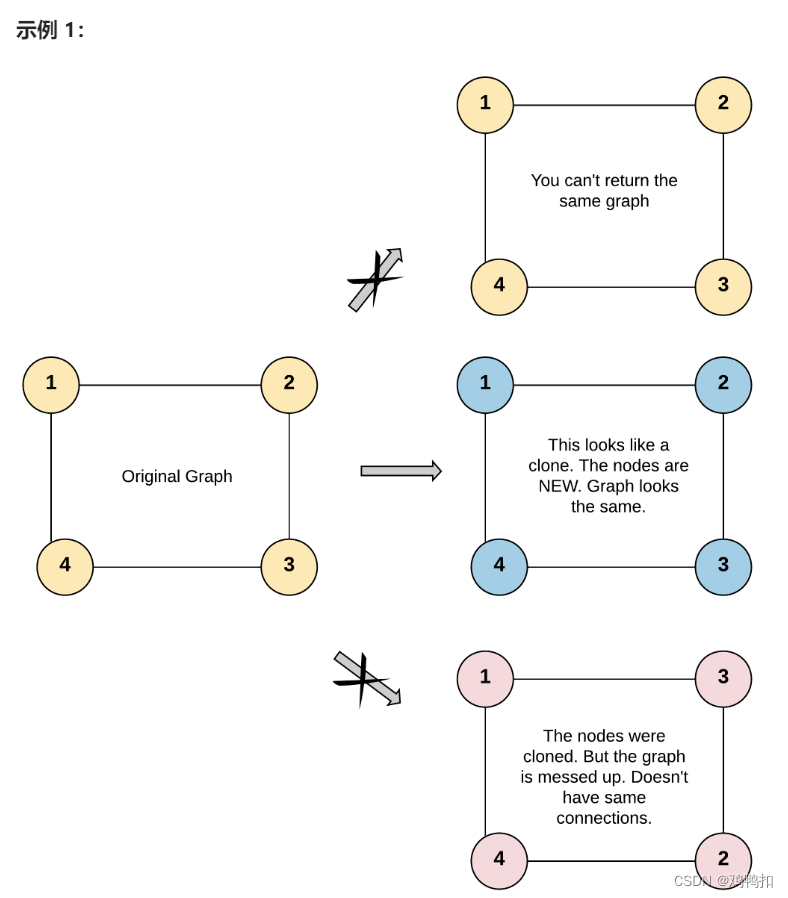
输入：adjList = [[2,4],[1,3],[2,4],[1,3]]
输出：[[2,4],[1,3],[2,4],[1,3]]
解释：
图中有 4 个节点。
节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

示例 2：
输入：adjList = [[]]
输出：[[]]
解释：输入包含一个空列表。该图仅仅只有一个值为 1 的节点，它没有任何邻居。
示例 3：

输入：adjList = []
输出：[]
解释：这个图是空的，它不含任何节点。

提示：

节点数不超过 100 。
每个节点值 Node.val 都是唯一的，1 <= Node.val <= 100。
无向图是一个简单图，这意味着图中没有重复的边，也没有自环。
由于图是无向的，如果节点 p 是节点 q 的邻居，那么节点 q 也必须是节点 p 的邻居。
图是连通图，你可以从给定节点访问到所有节点。

思路

图的深拷贝可以由dfs或者bfs实现。但是需要注意：在这里的set不再是HashSet，因为它不是存储这个节点是否访问过。而是直接存储原节点和克隆节点的地址的键值对。因为图是无向图，或者说，双向图，所以访问过的节点也可能要再次处理的。譬如节点1的邻居是节点2，那么我们遍历节点1时，会增加“节点1->节点2”。但是如果只是看是否访问过时，遍历到节点2时就会因为访问过节点1而丧失掉“节点2->节点1”的这条边。

这道题用bfs会好一点。因为它是个存在环的无向图，bfs不存在回溯的情况，可以保证每个节点只被遍历一次，譬如遍历到节点1
时，直接构建节点1和其原有邻居列表的邻居关系，那么节点1为出发点的所有单边情况都构建好了。之后分别遍历到节点2和节点4时，也会将节点1为接受点的所有单边情况都构建好。所以刚好双边都能不多不少不重不漏地构建完。

但是dfs不同，因为dfs的每个节点不止会被只遍历一次，因为它要回溯。所以可能出现邻居节点重复添加的情况，所以构建邻居关系时比bfs需要多一步判重。
譬如开始时节点1先克隆并入栈。它原来的邻居节点有节点2和节点4，因为节点2没有被克隆过，所以开始遍历节点2。

节点2遍历时，它原来的邻居节点有节点1和节点3，因为节点1被克隆过，所以会构建“节点2->节点1”的邻居关系。但是因为节点3没有被克隆过，所以开始遍历节点3。

==节点3遍历时，原有邻居有节点2和节点4，因为节点2被克隆过，所以会构建“节点3->节点2”==的邻居关系，但是因为节点4没有被克隆过，所以开始遍历节点4.。

节点4遍历时，原有邻居有节点3和节点1，因为节点1被克隆过，所以会构建“节点4->节点1”的邻居关系。同时节点3也被克隆过所以会构建“节点4->节点3”的邻居关系。然后开始遍历节点3。
节点3遍历时，原有邻居有节点2和节点4，因为节点2被克隆过，所以如果不判重，会多构建一个“节点3->节点2”的邻居关系。

bfs代码

class Solution {
    public Node cloneGraph(Node node) {
        if(node==null) return node;//直接返回node就好了，因为是空指针。
        HashMap<Node, Node> set = new HashMap<>();
        Queue<Node> queue = new LinkedList<>();
        set.put(node, cloneNode(node));
        queue.add(node);
        while(!queue.isEmpty()){
            Node cur = queue.poll();
            for(Node next: cur.neighbors){
                if(!set.containsKey(next)){//如果这个节点没有被克隆过
                    queue.add(next);//说明没有被遍历过，直接加入队列
                    set.put(next, cloneNode(next));//并加入set
                }
            set.get(cur).neighbors.add(set.get(next));//不管有没有被克隆过，因为每个节点只会被遍历一次，那么它的邻居节点都需要一次性加入该节点的邻居列表中。同时注意不是直接set.get(cur).neighbors.add(next)，而是set中next的克隆地址。
            }
        }
    return set.get(node);
    }
//这个函数，单纯地实现克隆功能，不连接邻居关系。
    private Node cloneNode(Node node){
        return new Node(node.val, new ArrayList<>());
    }
}

26ms,击败25.12%使用 Java 的用户

说实话，待优化……

dfs代码

class Solution {
    public Node cloneGraph(Node node) {
        if(node==null) return node;
        HashMap<Node, Node> set = new HashMap<>();
        Stack<Node> stack = new Stack<>();
        set.put(node,cloneNode(node));
        stack.add(node);
        while(!stack.isEmpty()){
            Node cur = stack.pop();
            for(Node next: cur.neighbors){
                if(!set.containsKey(next)){//如果这个next节点没有被克隆过
                    stack.add(cur);//说明也没有被遍历过，为了不会回退到上次遍历过的节点，cur和next依次加入栈。
                    stack.add(next);
                    set.put(next,cloneNode(next)); //克隆next节点，放入set
                    break;
                }
                List<Node> list = set.get(cur).neighbors;//如果这个next节点已经有克隆过了，那么看是否需要构建当前节点和next节点的邻居关系
                if(!list.contains(set.get(next))) set.get(cur).neighbors.add(set.get(next));//如果之前已经有过当前节点和next节点的邻居关系，说明我们不是第一次遍历到当前节点，而是回溯过程中遇到的当前节点，所以不再需要构建邻居关系。
            }
        }
        return set.get(node);
    }

    public Node cloneNode(Node node){
        return new Node(node.val, new ArrayList<>());
    }
}

27ms,击败15.19%使用 Java 的用户

依旧待优化……