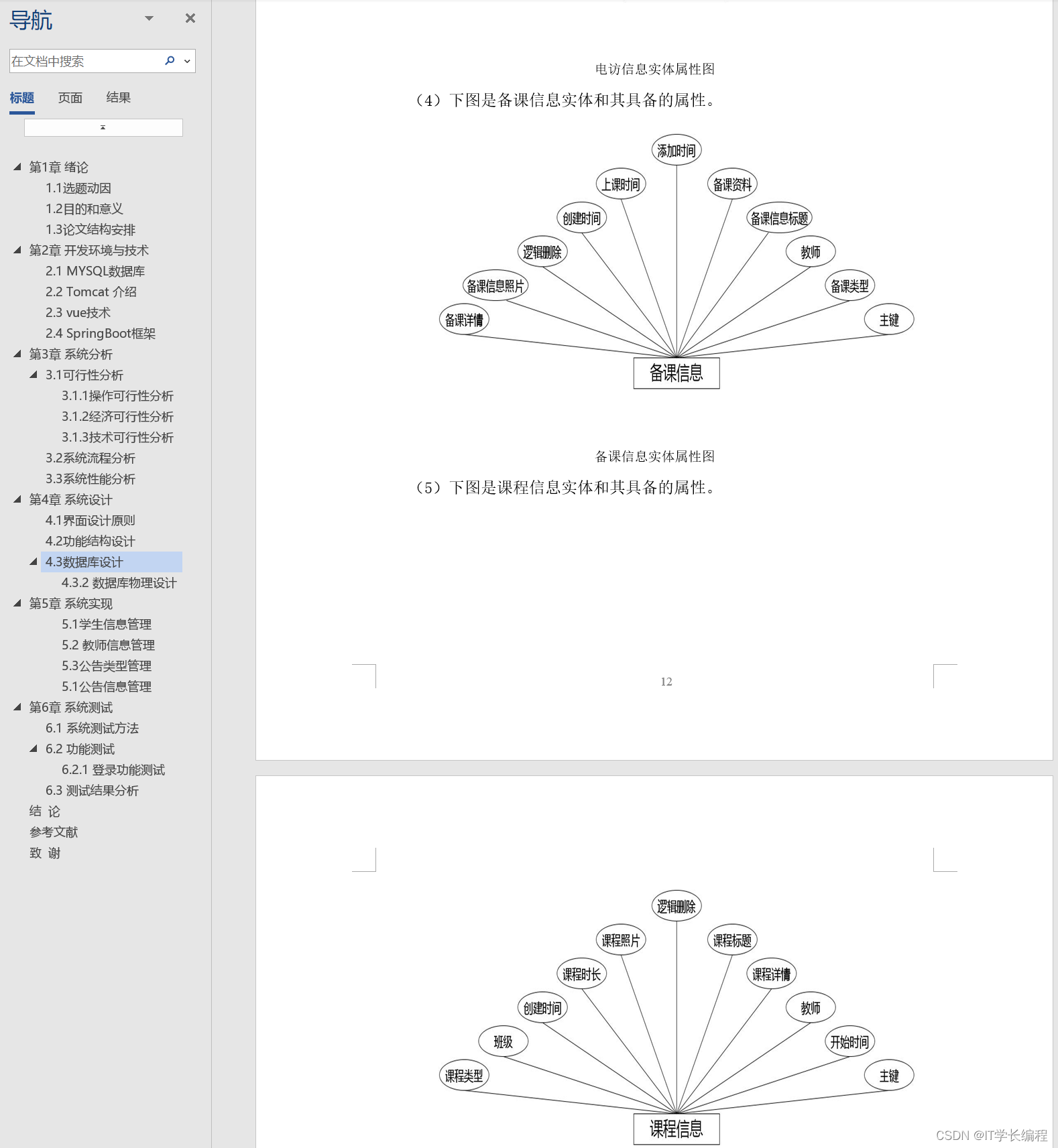
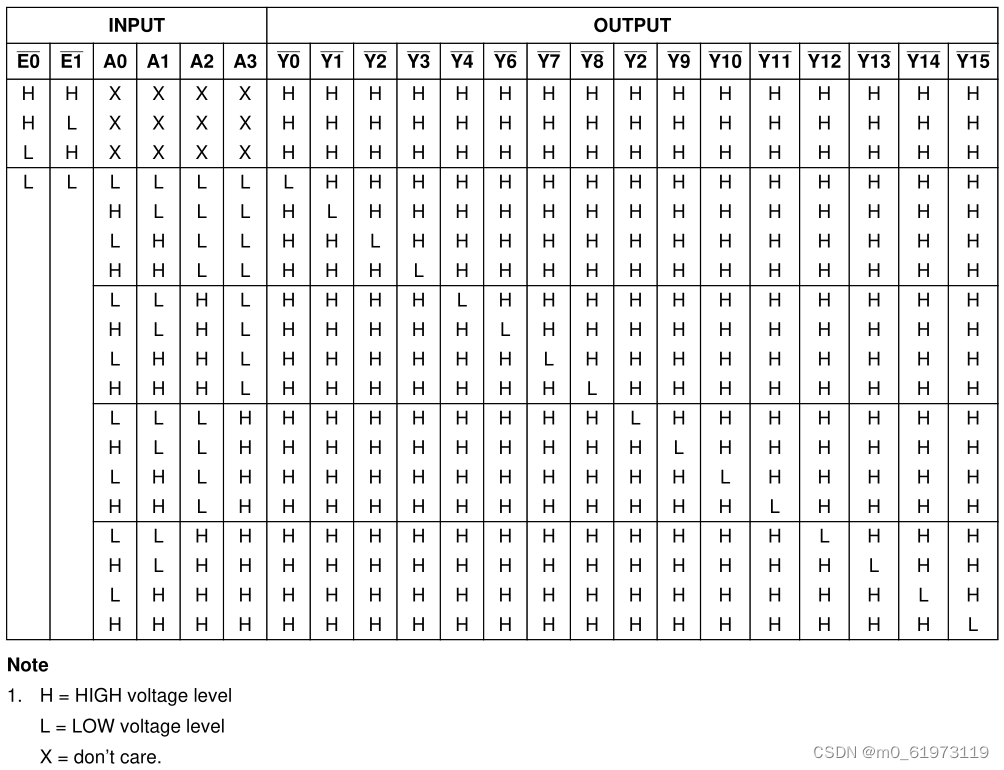
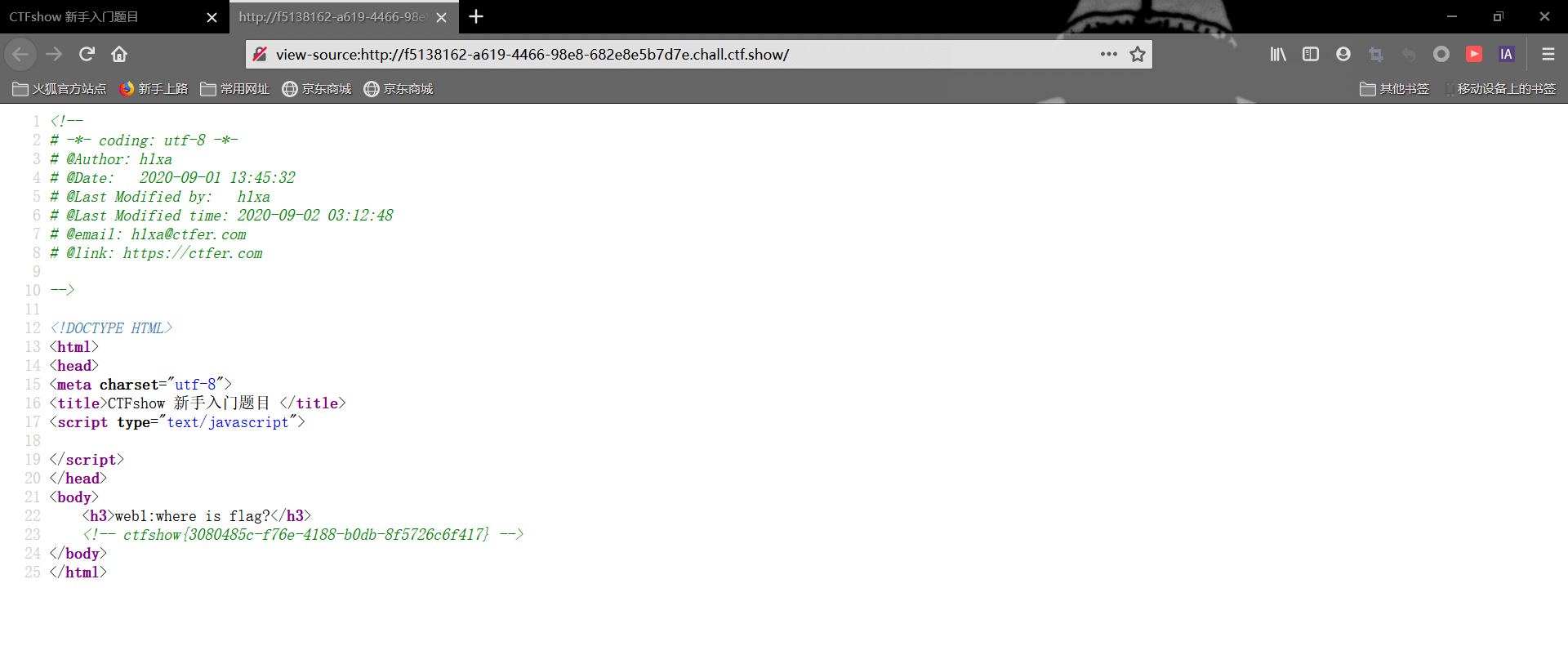
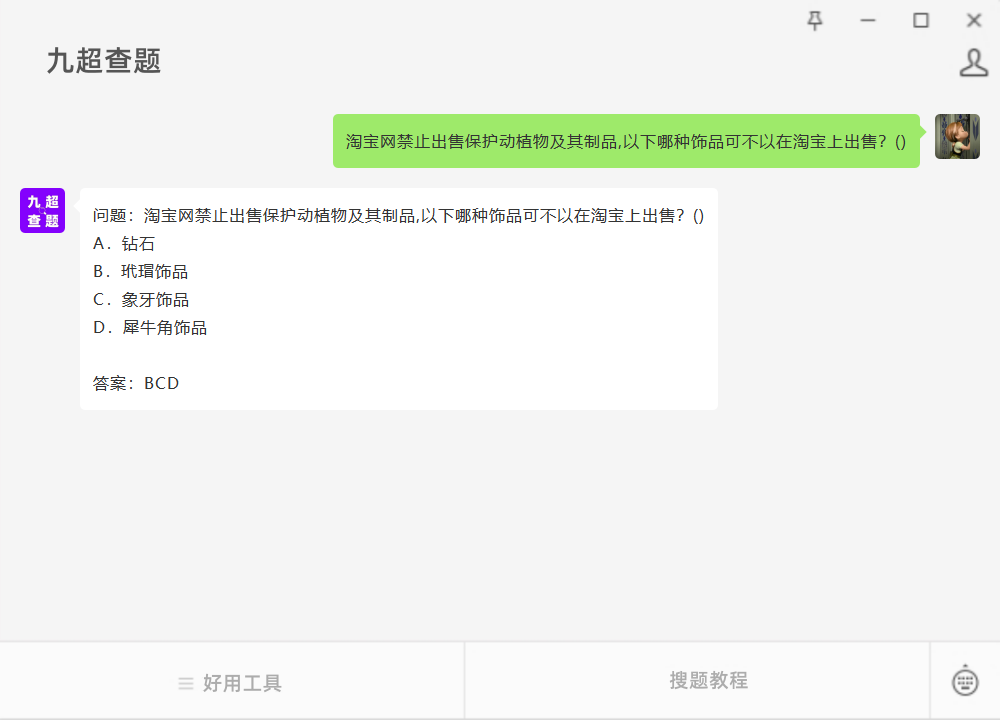
损失函数,用来衡量预测值和真实值之间的区别。是机器学习里面一个非常重要的概念。
三个常用的损失函数 L2 loss、L1 loss、Huber’s Robust loss
均方损失 L2 Loss
l
(
y
,
y
′
)
=
1
2
(
y
−
y
′
)
2
l(y,y^{\prime})=\frac{1}{2}(y-y^{\prime})^{2}
l(y,y′)=21(y−y′)2
(除以
2
2
2的时候,
2
2
2和
1
2
\frac{1}{2}
21相互抵消。)
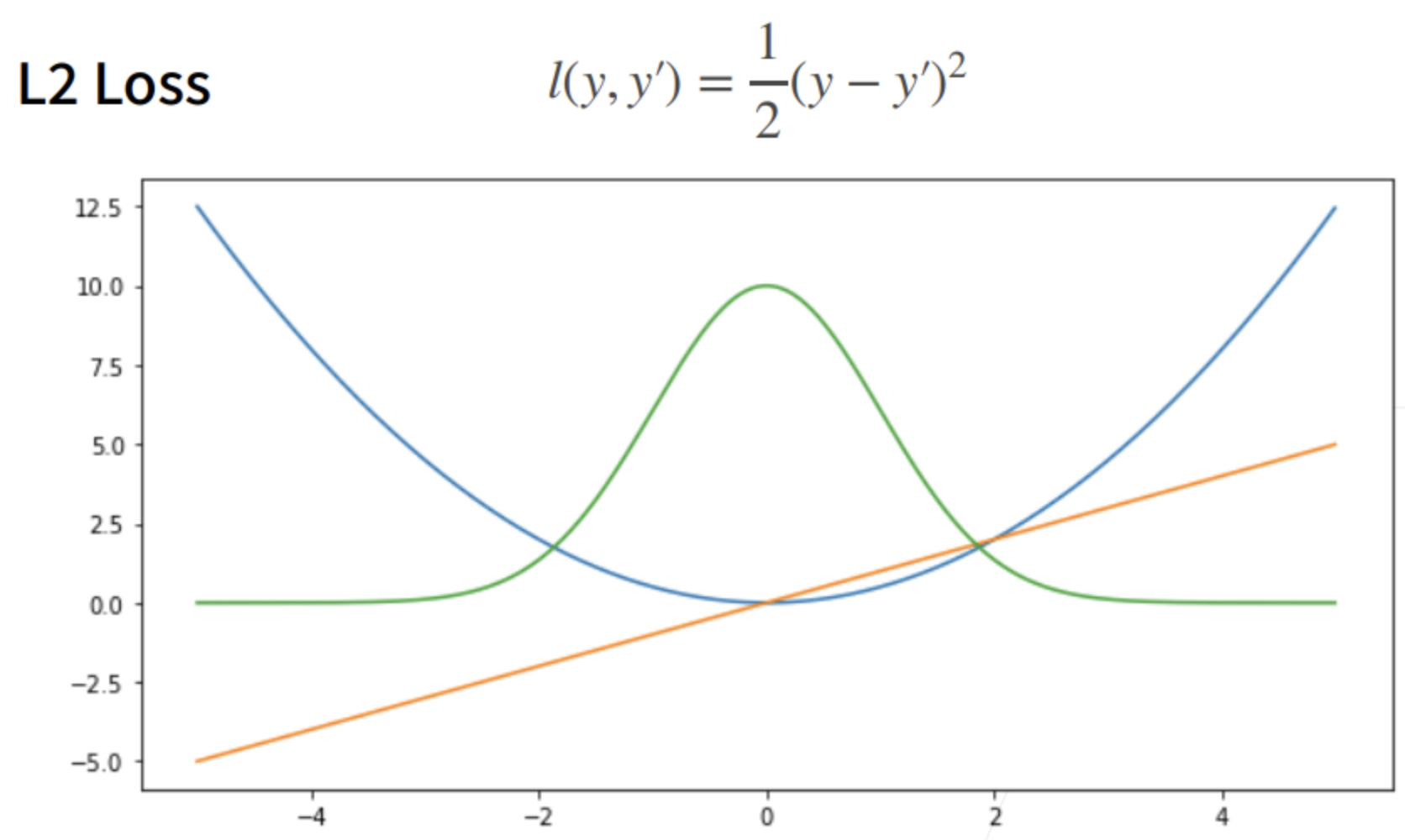

这里说的梯度,其实是经过了一次取绝对值。
绝对值损失函数 L1 Loss
l ( y , y ′ ) = | y − y ′ | l(y,y^{\prime})=|y-y^{\prime}| l(y,y′)=|y−y′|
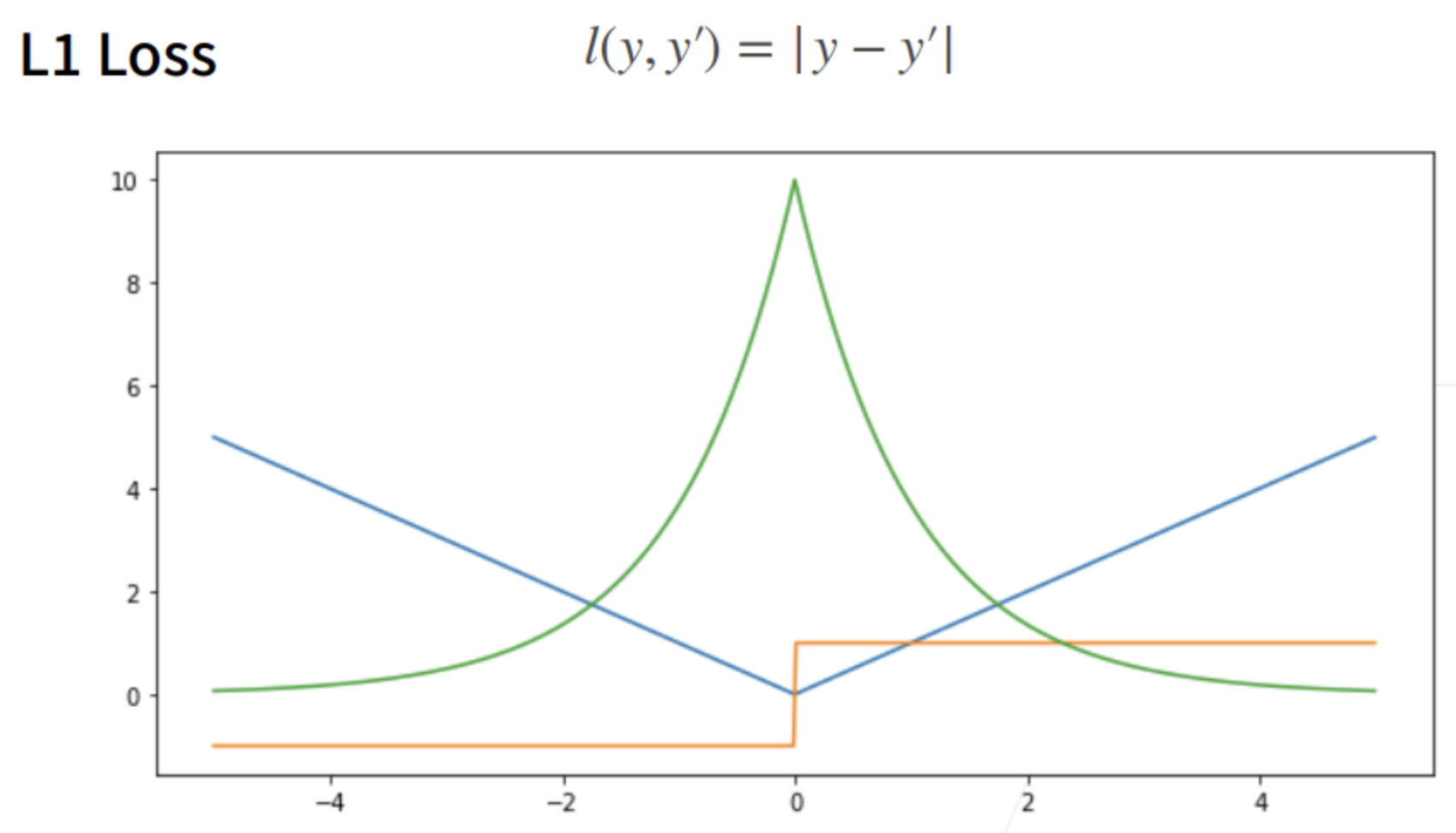
① 相对L2 loss,L1 loss的梯度就是远离原点时,梯度也不是特别大,权重的更新也不是特别大。会带来很多稳定性的好处。不管离原点多远(预测值和真实值相差多大),梯度它总是以同样的粒度后撤。
② 它的缺点是在零点处不可导,并在零点处左右有±1的变化,这个不平滑性导致预测值与真实值靠的比较近的时候,优化到末期的时候,可能会不那么稳定。
Huber’s Robust loss
l
(
y
,
y
′
)
=
{
∣
y
−
y
′
∣
−
1
2
,
i
f
∣
y
−
y
′
∣
>
1
1
2
(
y
−
y
′
)
2
,
o
t
h
e
r
w
i
s
e
l(y,y^{\prime})= \begin{cases} |y-y^{\prime}|-\frac{1} {2 } ,\quad if \ |y-y^{\prime}|>1\\ \frac{1}{2}(y-y^{\prime})^{2}, \quad \ \ otherwise \end{cases}
l(y,y′)={∣y−y′∣−21,if ∣y−y′∣>121(y−y′)2, otherwise当真实值和预测值的差大于
1
1
1的时候,损失函数是一个绝对值误差;当真实值和预测值的差小于
1
1
1的时候,损失函数是一个均方误差。(绝对值误差减去二分之一,是为了把曲线连起来)

在
+
1
+1
+1和
−
1
-1
−1之间是一个二次函数,在之外是两条直线。
好处:
- 当预测值和真实值差的比较远的时候,不管怎样,它都会以一个比较均匀的梯度往回撤。
- 在预测值和真实值差的比较小的时候,可以保证梯度下降优化是比较平滑的。