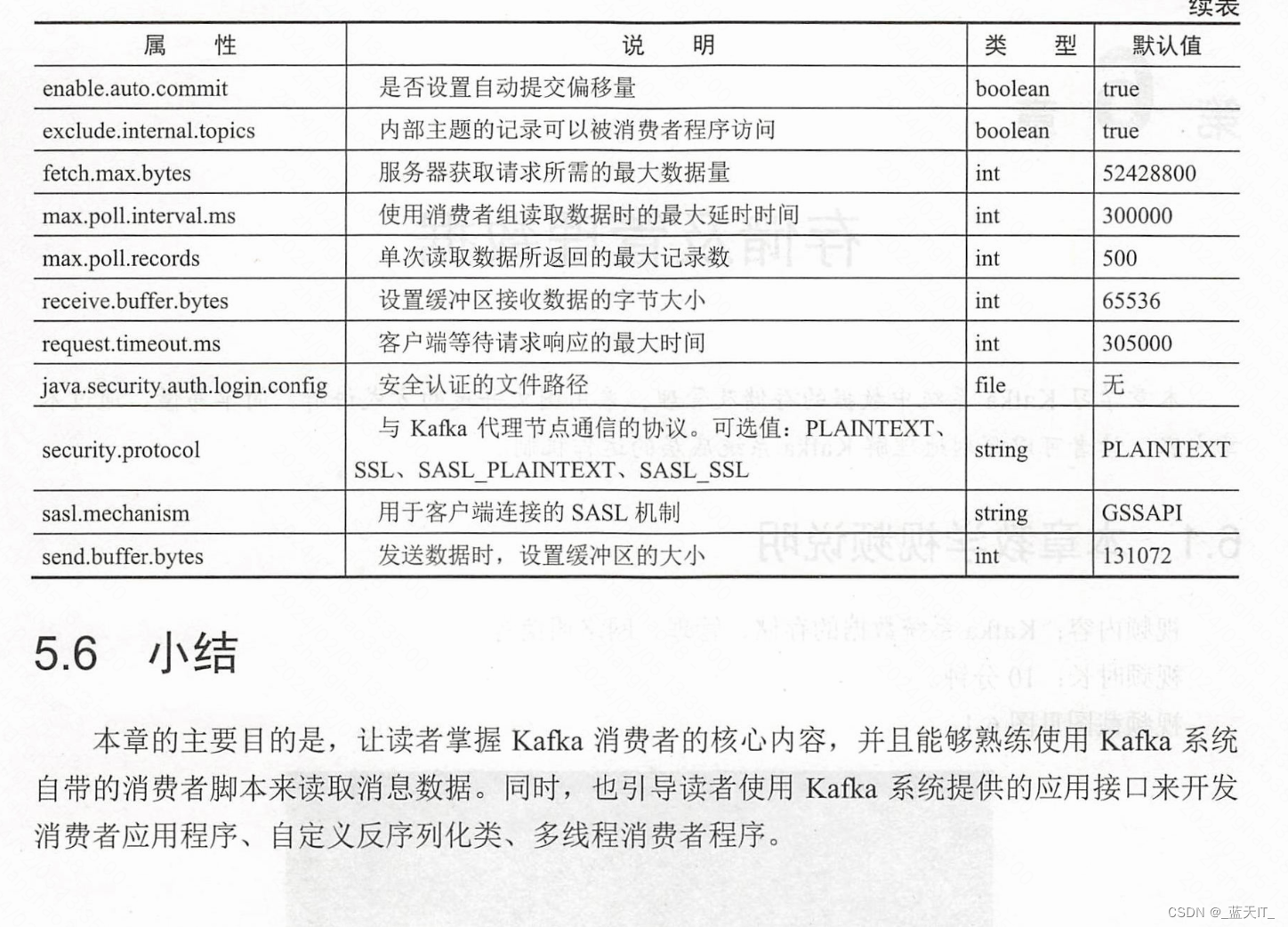
题目描述：

这里有个小trick
当时也看到数据范围的问题了
$n是1e6{\sum }_{i=1}^{n}a[i]<=5e7$
我们考虑不同的数$12...k-1k$
$sum=(1+k)\ast k/2$
不同的数最多有$n^2$个
$O(k^2)$统计贡献

#include <bits/stdc++.h> 
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back

using namespace std;

void solve()
{
	int n;cin>>n;
	map<int,int>p;
	
	//map去重
	rep(i,1,n){
		int x;cin>>x;
		p[x]++;
	}
	
	//统计贡献
	int ans=0;
	const int mod=998244353;
	for(auto [i,cnt1]:p){
		for(auto [j,cnt2]:p){
			ans=(ans+__gcd(i,j)*(__builtin_popcount(i)+__builtin_popcount(j))%mod*cnt1%mod*cnt2%mod)%mod;
		}
	}
	cout<<ans<<endl;
}
signed main()
{
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//   	freopen("1.in", "r", stdin);
  	int _;
//	cin>>_;
//	while(_--)
	solve();
	return 0;
}