最常见的算法——梯度下降
当一个模型没有显示解的时候,该怎么办呢?
- 首先挑选一个参数的随机初始值,可以随便在什么地方都没关系,然后记为 w 0 \pmb{w_{0}} w0
- 在接下来的时刻里面,我们不断的去更新 w 0 \pmb{w_{0}} w0,使得它接近我们的最优解
具体来说:
- 挑选一个初始值 w 0 \pmb{w_{0}} w0
- 重复迭代参数
t
=
1
,
2
,
3
t = 1,2,3
t=1,2,3
w
t
=
w
t
−
1
−
η
∂
ℓ
∂
w
t
−
1
\pmb{w}_{t}=\pmb{w}_{t-1}-\eta \frac{\partial \ell}{\partial \pmb{w}_{t-1}}
wt=wt−1−η∂wt−1∂ℓ
η
\eta
η是一个标量(学习率,步长的超参数),
∂
ℓ
∂
w
t
−
1
\frac{\partial \ell}{\partial \pmb{w}_{t-1}}
∂wt−1∂ℓ是损失函数关于
w
t
−
1
\pmb{w_{t-1}}
wt−1处的梯度。
梯度是使得函数的值增加最快的方向,那么负梯度就是使得这个函数的值减少最快的方向。
学习率是指每次我沿着这个负梯度的方向走多远
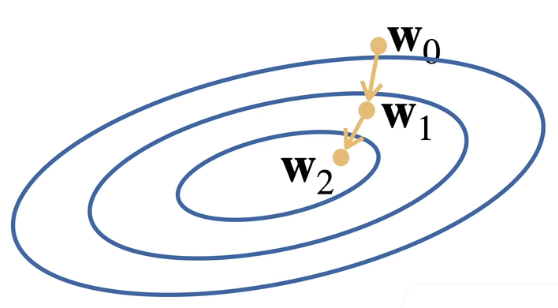
直观的从图上来看,这个类似一个地理中的等高线,在同一条等高线上的函数值是相同的。 − η ∂ ℓ ∂ w t − 1 -\eta \frac{\partial \ell}{\partial \pmb{w}_{t-1}} −η∂wt−1∂ℓ表示的是由 w 0 \pmb{w_{0}} w0到 w 1 \pmb{w_{1}} w1的这条向量(或者是由 w 1 \pmb{w_{1}} w1到 w 2 \pmb{w_{2}} w2的这条向量)。把 w 0 \pmb{w_{0}} w0和这个向量一加,就会到 w 1 \pmb{w_{1}} w1的位置。
学习率是指的步长,是我们人为选定的超参数。不能选的太小,也不能选的太大。
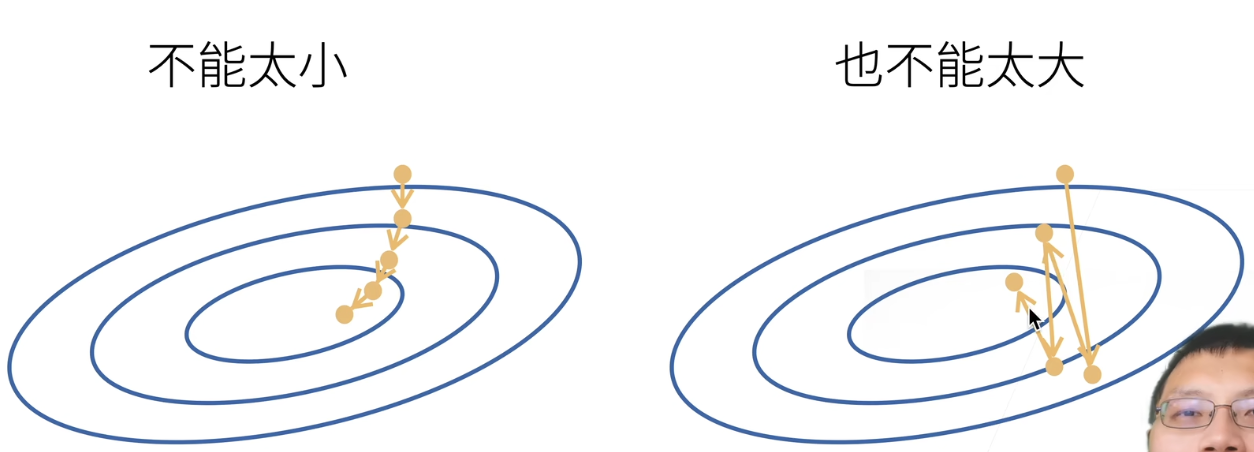
- 选的太小:每一次走的步长很有限,我们到达一个点需要走很多步,这不是一个很好的事情。计算梯度是一件很贵的事情,是整个模型训练中最贵的部分,所以我们要尽可能的少去计算梯度。
- 选的太大:一下子步子迈得太大,会使得我们一直在震荡,并没有在严格下降。
更常见的算法——小批量随机梯度下降
-
在整个训练集上算梯度太贵了
一个深度神经网络模型可能需要数分钟至数小时 -
我们可以随机采样 b b b个样本 i 1 , i 2 , . . . , i b i_{1},i_{2},...,i_{b} i1,i2,...,ib来近似损失(用 b b b个样本的平均损失来近似所有 n n n个样本的平均损失)
1 b ∑ i ∈ I b ℓ ( x i , y i , w ) \frac{1}{b}\sum_{i\in I_{b}}\ell(\pmb{x}_{i},y_{i},\pmb{w}) b1i∈Ib∑ℓ(xi,yi,w)
b b b是批量大小,另一个重要的超参数。
当 b b b很大的时候,近似很精确,当 b b b很小的时候,近似不那么精确,但是计算它的梯度很容易,梯度计算的复杂度与样本的个数线性相关。 -
批量不能太小:每次计算量太小,不适合并行来最大化利用计算资源(深度学习模型会用GPU来计算,但批量太小不能有效利用GPU并行计算)
-
批量不能太大:内存消耗增加,浪费计算,例如如果所有的样本都是相同的
总结
- 梯度下降通过不断沿着反梯度方向更新参数求解
- 小批量随机梯度下降是深度学习默认的求解算法
- 两个重要的超参数是批量大小和学习率