1 洛布数(Lobb Number)
在组合数学中,洛布数(Lobb Number)L(m,n)计算n+m开括号的排列方式,以形成一个有效的平衡括号序列的开始。
Lobb数由两个非负整数m和n参数化,其中n>=m>=0。
可通过以下方式获得:
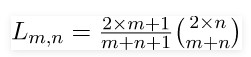
洛布数(Lobb Number)还用于计算将值+1的n+m个副本和值-1的n–m个副本排列成一个序列的方式的数量,以便序列的所有部分和都是非负的。
读取来特别拗口,看代码吧。
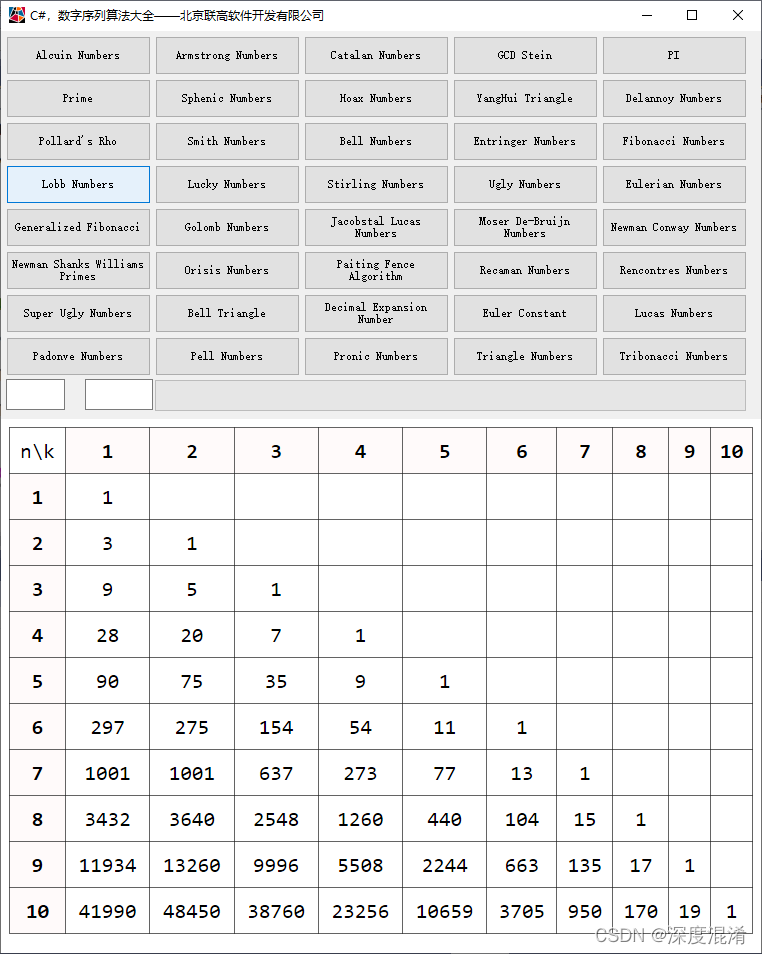
源程序:
2 源代码
using System;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Number_Sequence
{
private static int Binomial_Coeff(int n, int k)
{
int[,] Coeff = new int[n + 1, k + 1];
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= Math.Min(i, k); j++)
{
if (j == 0 || j == i)
{
Coeff[i, j] = 1;
}
else
{
Coeff[i, j] = Coeff[i - 1, j - 1] + Coeff[i - 1, j];
}
}
}
return Coeff[n, k];
}
public static int Lobb_Number(int n, int m)
{
return ((2 * m + 1) * Binomial_Coeff(2 * n, m + n)) / (m + n + 1);
}
}
}
——————————————————
POWER BY TRUFFER.CN
3 代码格式
using System;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Number_Sequence
{
private static int Binomial_Coeff(int n, int k)
{
int[,] Coeff = new int[n + 1, k + 1];
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= Math.Min(i, k); j++)
{
if (j == 0 || j == i)
{
Coeff[i, j] = 1;
}
else
{
Coeff[i, j] = Coeff[i - 1, j - 1] + Coeff[i - 1, j];
}
}
}
return Coeff[n, k];
}
public static int Lobb_Number(int n, int m)
{
return ((2 * m + 1) * Binomial_Coeff(2 * n, m + n)) / (m + n + 1);
}
}
}