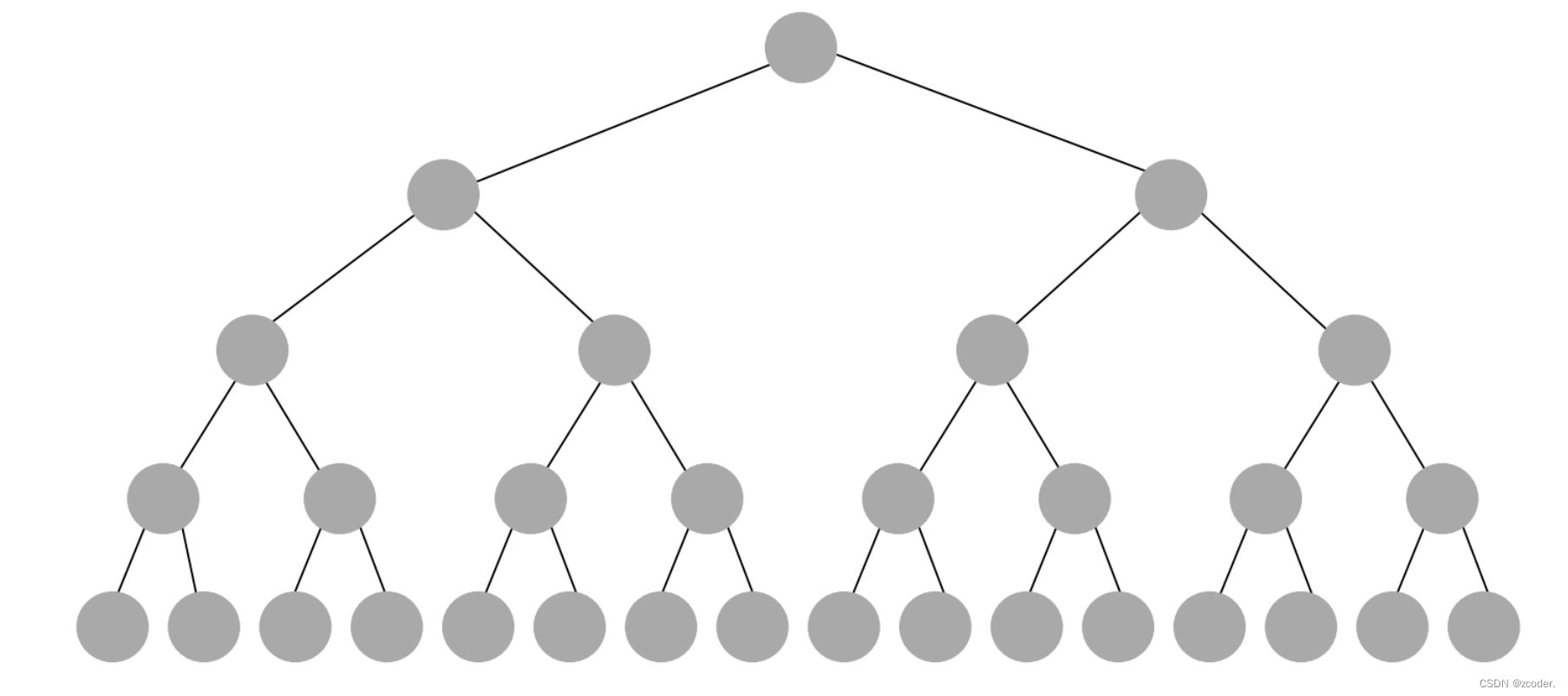
树

struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x): val(x), left(nullptr), right(nullptr) {}
}
二叉树的遍历
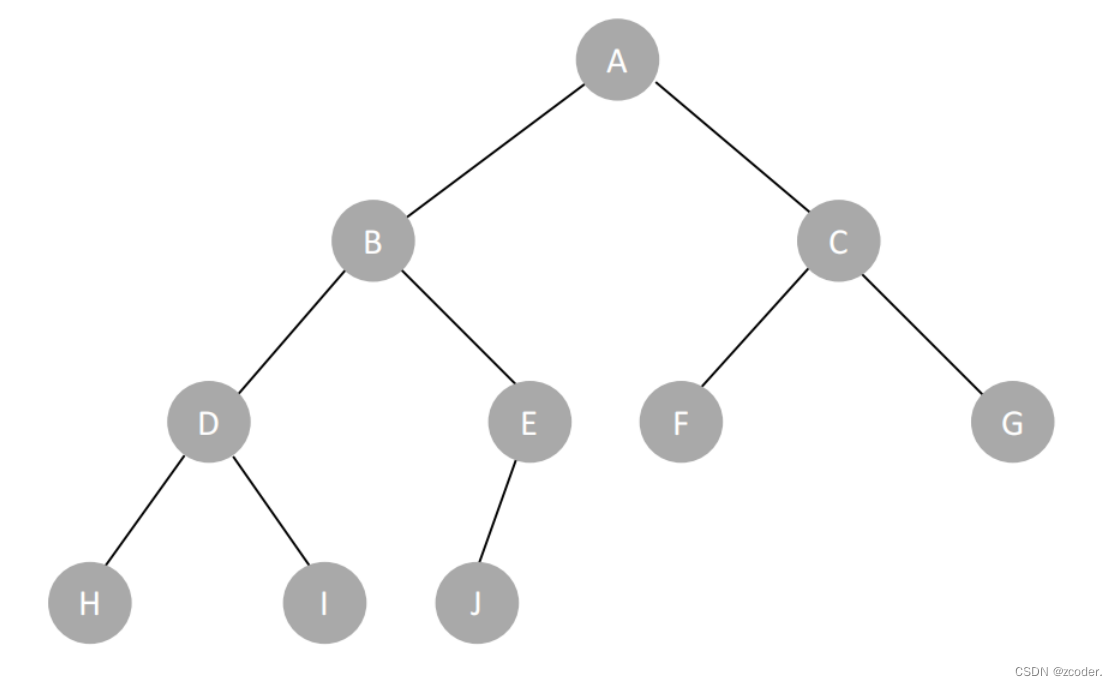
- 前序 Pre-Order:根 - 左子树 - 右子树:A BDHIEJ
CFG - 中序 In-Order:左子树 - 根 - 右子树:HDIBJE A
FCG - 后序 Post-Order:左子树 - 右子树 - 根:HIDJEB
FGCA - 层次序:A
BCDEFG HIJ
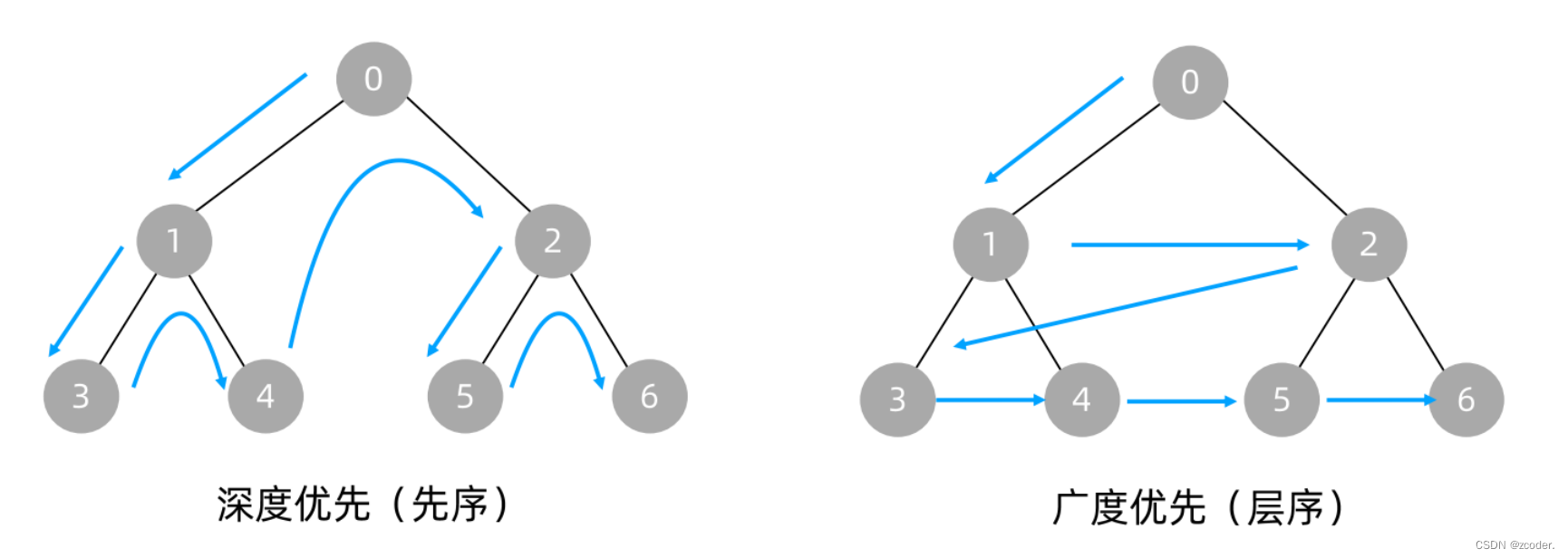
- 树的前序遍历又称树的
深度优先遍历 - 树的层序遍历又称树的
广度优先遍历
LeetCode 练习题
- 226. 翻转二叉树
- 98. 验证二叉搜索树
- 104. 二叉树的最大深度
- 111. 二叉树的最小深度
- 94. 二叉树的中序遍历
- 144. 二叉树的前序遍历
- 145. 二叉树的后序遍历
- 102. 二叉树的层序遍历
- 589. N 叉树的前序遍历
- 590. N 叉树的后序遍历
- 429. N 叉树的层序遍历
- 559. N 叉树的最大深度
- 297. 二叉树的序列化与反序列化
- 543. 二叉树的直径
- 236. 二叉树的最近公共祖先
基环树
- 向一棵树添加一条边,就形成了一个环
- 此时整个结构被称为基环树(pseudotree / unicycli graph)
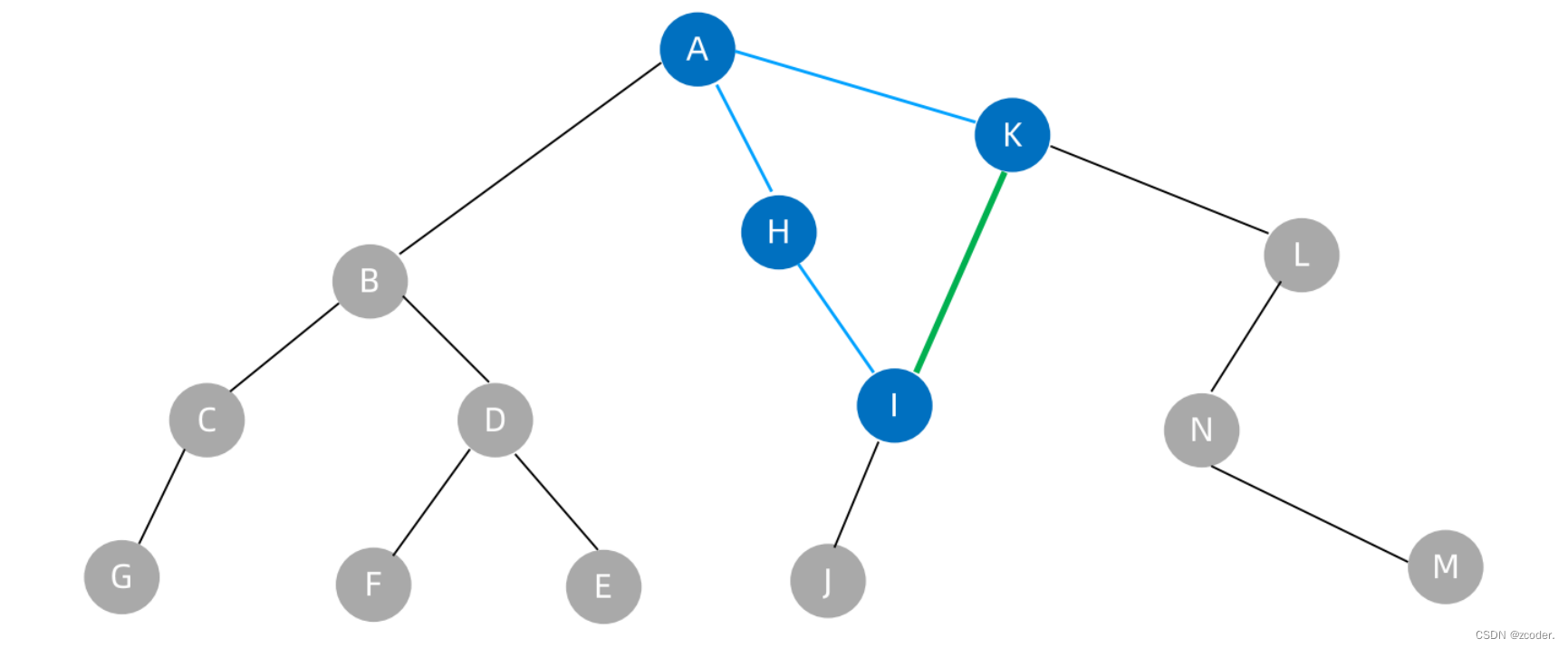
图
- 链表是特殊化的树
- 树是特殊化的图
- N 个点 N - 1 条边的连通无向图 - 树
- N 个点 N 条边的连通无向图 - 基环树
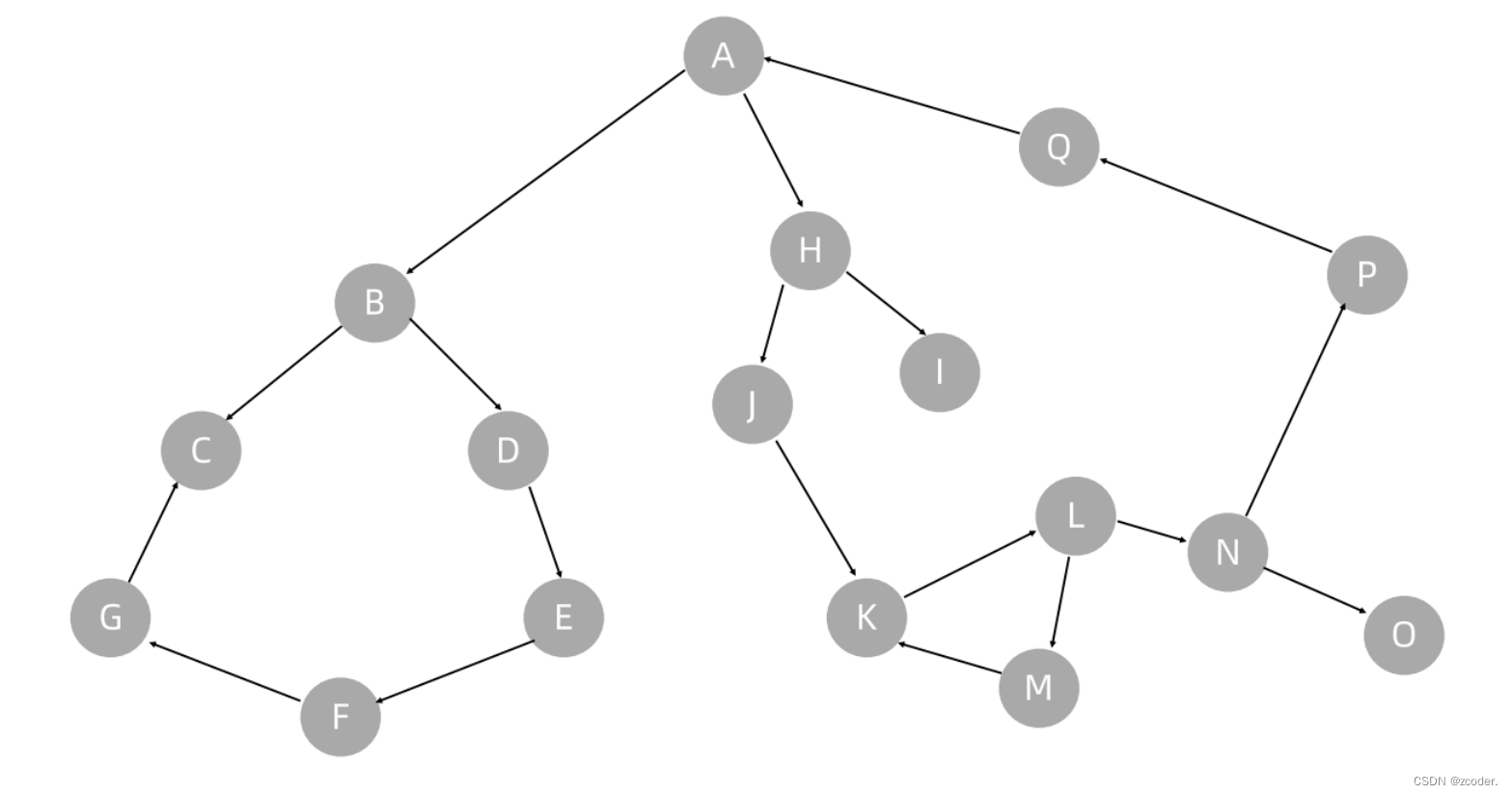
图的存储
- 定义
- 邻接矩阵
O
(
n
2
)
O(n^2)
O(n2):
int graph[MAX_N][MAX_N]; - 出边数组
O
(
n
+
m
)
O(n + m)
O(n+m):
vector<int> graph[MAX_N]; vector<vector<int>> graph; - 邻接表
O
(
n
+
m
)
O(n + m)
O(n+m):
struct Node { int to; Node* next; }; Node* head[MAX_N];
- 邻接矩阵
O
(
n
2
)
O(n^2)
O(n2):
- 新增边
(
x
,
y
)
(x, y)
(x,y)
- 邻接矩阵:
graph[x][y] = 1; - 出边数组:
graph[x].push_back(y); - 邻接表:
Node * node = new Node(); node->to = y; node->next = head[x]; head[x] = node;
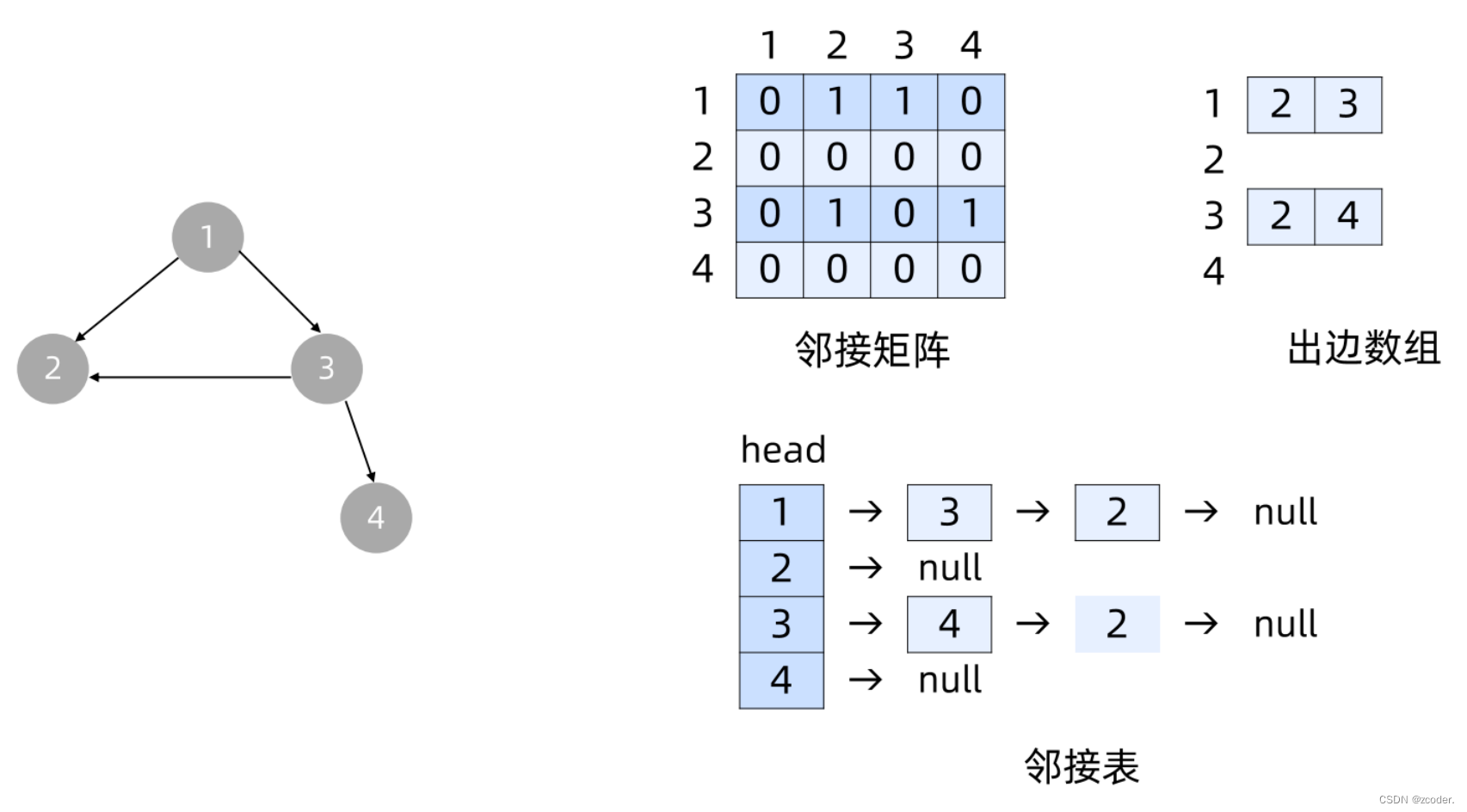
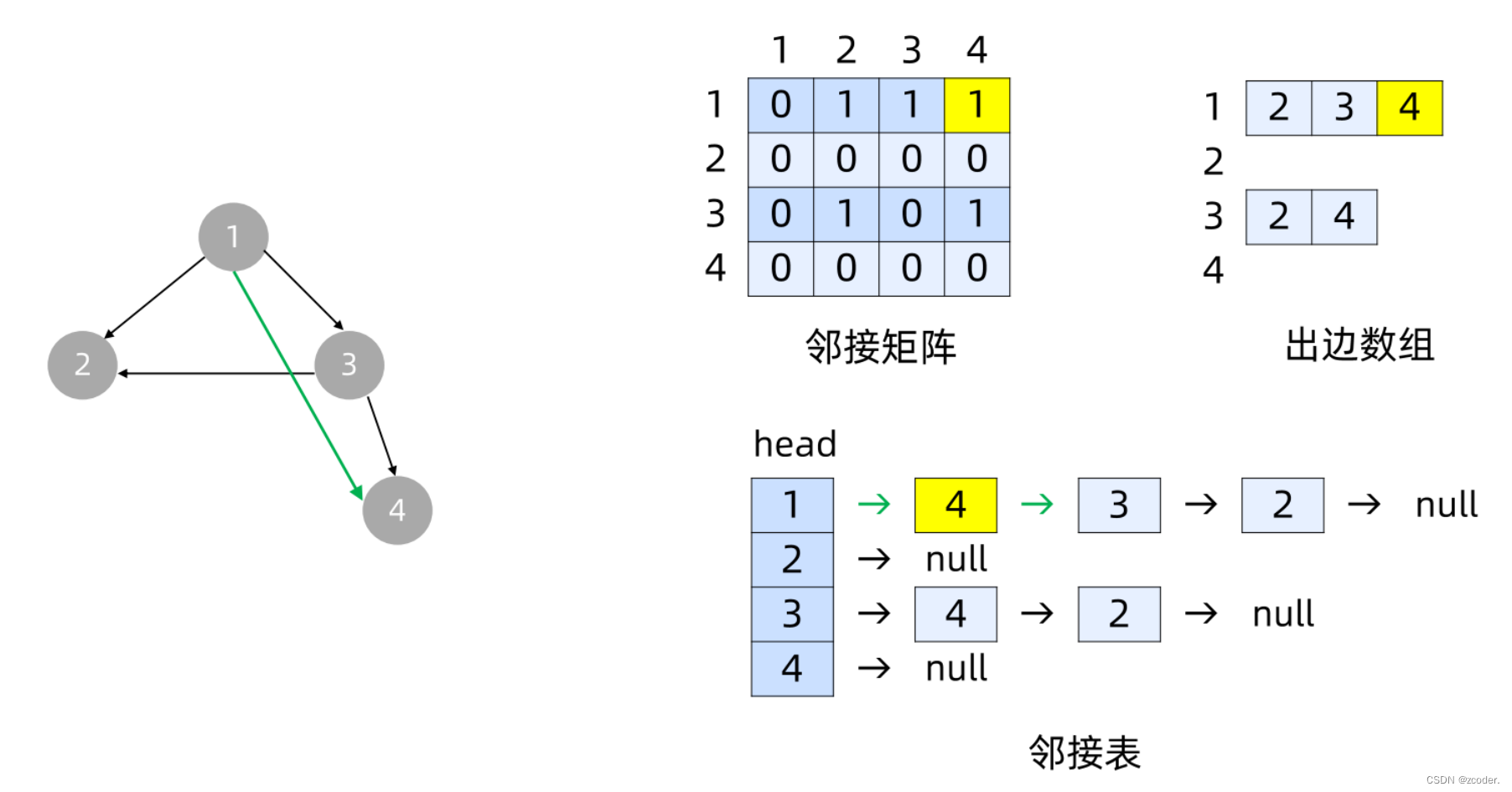
- 邻接矩阵:
图的遍历
-
深度优先遍历
- 划分连通块
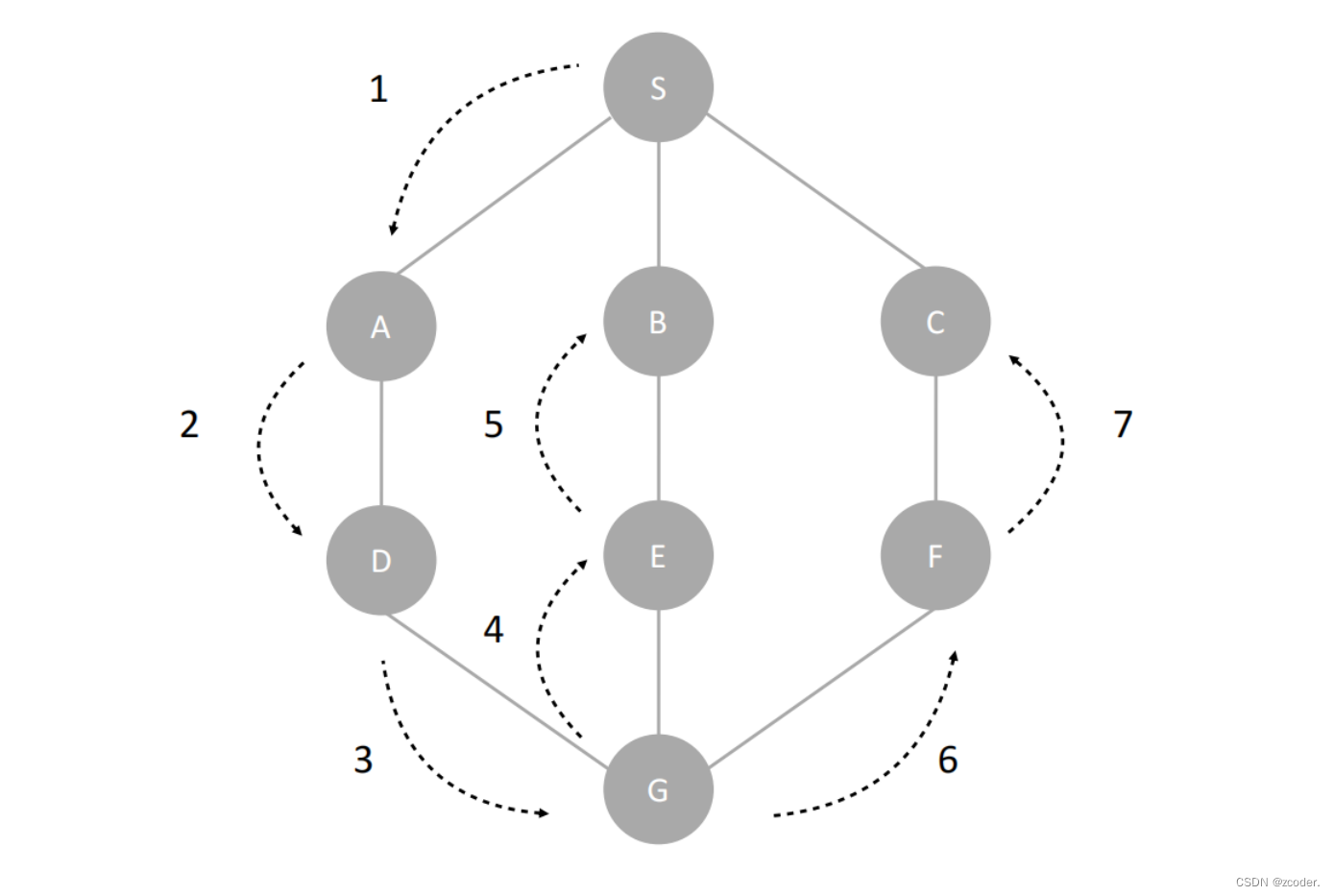
- 划分连通块
-
广度优先遍历
- 拓扑排序
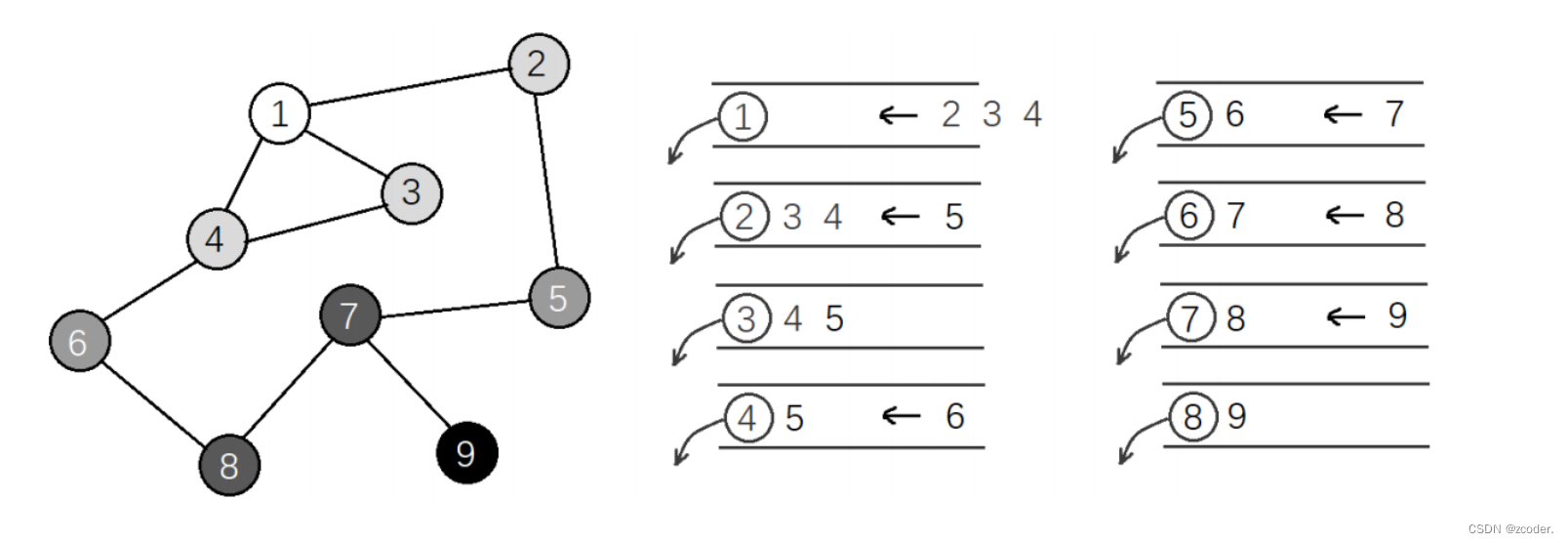
- 拓扑排序
LeetCode 练习题
- 684. 冗余连接
- 207. 课程表
- 210. 课程表 II
![[Vue3] useRoute、useRouter](https://img-blog.csdnimg.cn/direct/7df1ed7e6b9c4818a27d60e5f09e4a97.png)