问题引入

给定一个单向链表，怎么判断这个链表是否成环？如果这个链表是环形的，找到这个环形的起点。

@Getter
@Setter
public class ListNode {

    public Integer val;

    public ListNode next;

    public ListNode(Integer val) {

        this.val = val;
    }

    public ListNode(Integer val, ListNode next) {
        this.val = val;
        this.next = next;
    }

    public ListNode() {
    }
}

判断是否成环 

比如，下面这个就是一个典型的单向环形链表

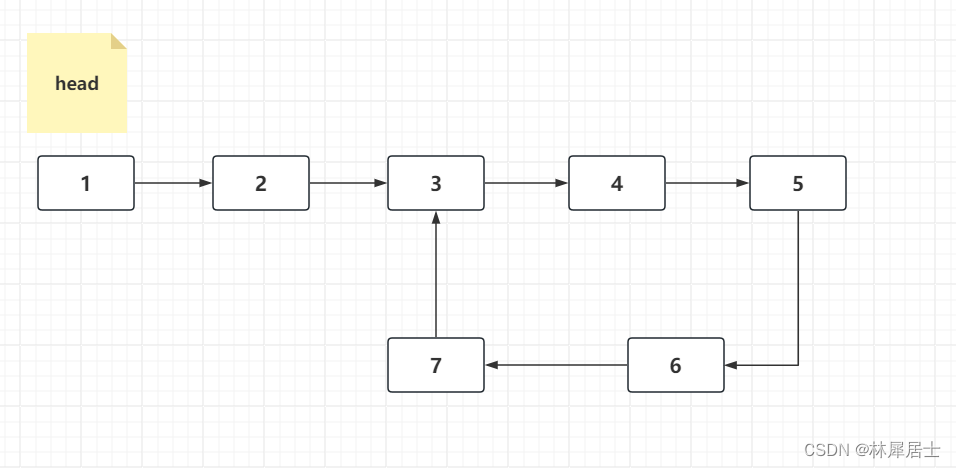
可以想象一下，大学里面的长跑比赛，赛道是环形的，那些跑的快的同学往往会领先跑的最慢的同学，随着时间的推移，他会在某个位置，领先一圈追上最慢的同学，如果长跑距离足够长，最快的同学还会第二次、第三次超越最慢的同学。

受此启发，我们是不是可以模拟两个遍历速度不同的指针来解决此问题，答案是可行的。比较官方的说法是快慢指针。

原理也很简单，快指针一次走两步，慢指针一次走一步，如果快指针最终和慢指针相遇了，说明这个链表是成环的，相反，快指针直接遍历到了终点【下一个节点为null】还没有相遇，说明此链表不是环形的。

直接看代码吧

public static boolean hasCycle(ListNode head) {
        ListNode fast = head, slow = head;
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
            //快指针追上了慢指针
            if (fast == slow) {
                return true;
            }
        }

        return false;

    }

找到环的起点

对于这个问题，我们需要先推演一下

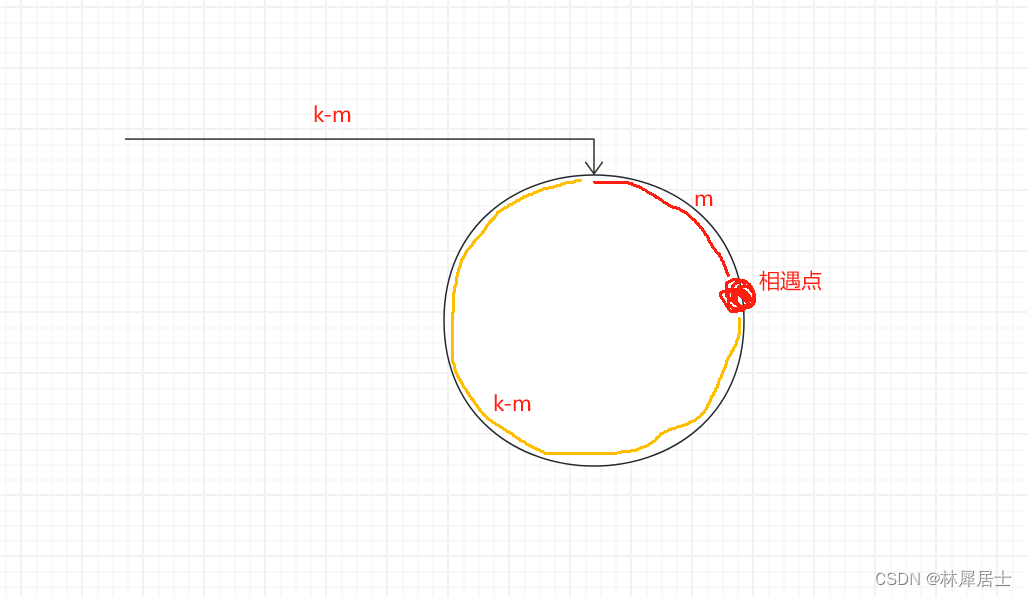
假设快慢指针在如图中的红色点处第一次相遇，那么 是不是可以认为快指针比慢指针多走了一圈。假设从环的起点到红色点处的链表长度是m，假设慢指针一共走了k步，那么快指针一共则走了2k步，根据上面的推演可以看出

相遇点距离环的起点是k-m步，和链表的起点到环的起点处的距离是一样的，假如在快慢指针第一次相遇的时候，慢指针返回至链表的起点，同时快指针的速度降为和慢指针一样，那么他们下一次相遇点一定是在环的起点。

对应的程序代码如下

    public static ListNode detectCycle(ListNode head) {
        ListNode fast, slow;
        fast = slow = head;
        while (fast != null && fast.next != null) {
            //快指针走两步
            fast = fast.next.next;
            //满指针走一步
            slow = slow.next;
            if (fast == slow) {
                break;
            }
        }

        if (fast == null || fast.next == null) {
            //没有成环
            return null;
        }

        //慢指针回到链表的头部
        slow = head;
        while (slow != fast) {
            //快慢指针步调一致
            slow = slow.next;
            fast = fast.next;
        }

        return slow;
    }

有没有觉得很神奇，解决问题的思路就来源于生活，道存天地间！