数据结构——用Java实现二分搜索树

news2024/12/23 8:44:56

目录

一、树

二、二分搜索树

1.二叉树

2.二分搜索树

三、代码实现

1.树的构建

2.获取树中结点的个数

3.添加元素

4.查找元素

（1）查找元素是否存在

（2）查找最小元素

（3）查找最大元素

5.二分搜索树的遍历

（1）前序遍历：

（2）中序遍历：

（3）后序遍历：

（4）层序遍历：

6.删除操作

（1）删除最小元素

（2）删除最大元素

（3）删除任意元素

（4）删除根节点

一、树

        树结构本身是一种天然的组织结构

        是一个高效的查询内容的结构

二、二分搜索树

1.二叉树

特点：1.只有唯一的一个根节点

           2.每个结点最多有两个孩子

           3.每个结点最多有一个父亲

           4.二叉树具有天然的递归结构（左右子树也是二叉树）

           5.叶子结点出现在二叉树的最底层，除叶子结点之外的其它结点都有两个孩子结点。

2.二分搜索树

是特殊的二叉树

每个节点都大于左子树的所有结点，都小于右子树的所有结点

注意：存储的元素必须具有可比性

因为二分搜索树也是二叉树，也具有天然的递归结构，所以许多方法都可以使用递归的思想去实现

三、代码实现

1.树的构建

需要的元素有：根节点，结点，频率（如果添加的元素有重复元素），结点的值，索引，结点个数

//树的结点
    private static class Node<T> {
        private final T ele;//结点的值
        private int frequence;//频率
        private Node<T> left, right;//分别指向左右孩子的索引

        public Node(T ele) {
            this.ele = ele;
            this.left = this.right = null;
        }

    }

    //树对应的属性
    private Node<T> root;//树的根节点
    private int size;//结点的个数

    //构建树
    public BinearySeachTree() {
        this.root = null;
        this.size = 0;
    }

在给元素添加泛型后，就不能直接比较，所以在开始就继承Comparable来实现元素的比较

public class BinearySeachTree<T extends Comparable<T>>{

}

2.获取树中结点的个数

//获取树中结点的个数
    public int getSize() {
        return this.size;
    }

3.添加元素

将元素添加到二分搜索树的过程中，要注意将大的元素放在结点的右边，小的元素放在左边

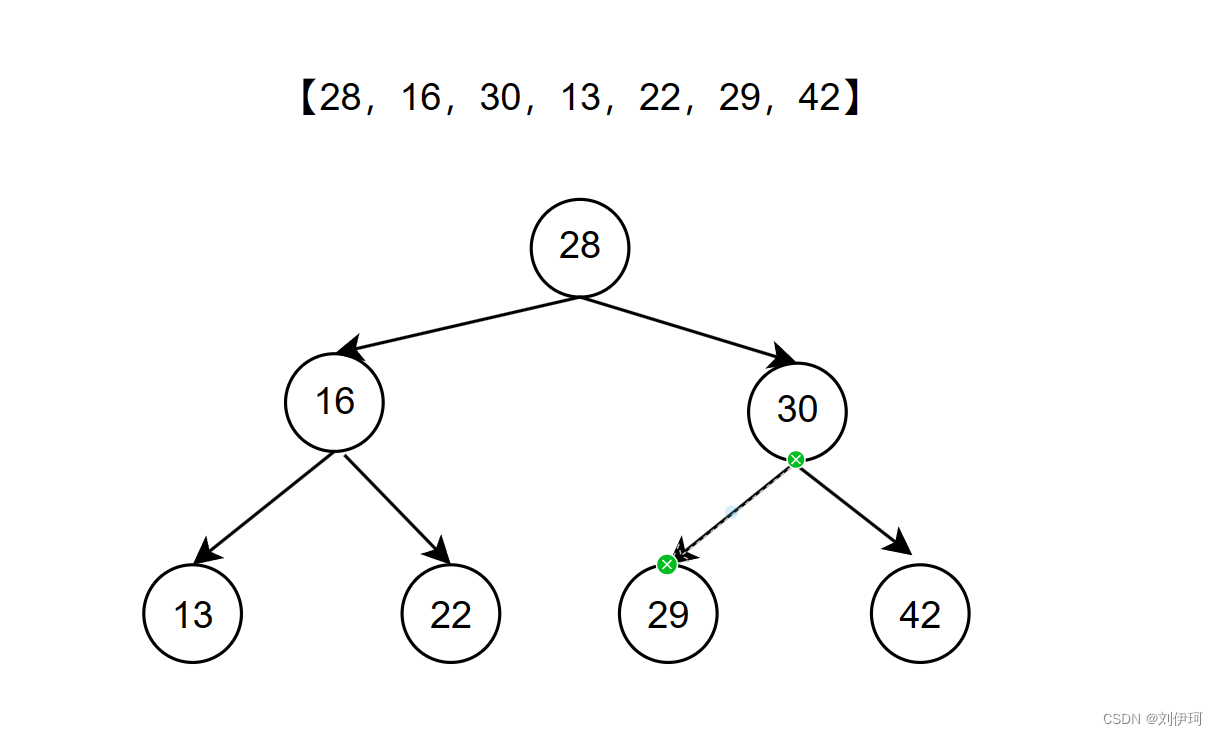
再添加元素时，需要找到对应的位置，则可以使用递归的思想。

如果添加的值小于结点的值，则查找结点左孩子，如果还是小于结点，则继续查找

//向树中添加结点
    public void add(T ele) {
        //更新根结点
        this.root = addDG(this.root, ele);
    }

    //语义：向以root为根的二分搜索树中添加元素ele
    private Node<T> addDG(Node<T> root, T ele) {
        //递归终止条件
        if (root == null) {
            this.size++;
            return new Node<T>(ele);
        }
        //递归操作
        if (root.ele.compareTo(ele) > 0) {
            root.left = addDG(root.left, ele);
        } else if (root.ele.compareTo(ele) < 0) {
            root.right = addDG(root.right, ele);
        } else {
            //更新频率
            root.frequence++;
        }
        return root;
    }

4.查找元素

（1）查找元素是否存在

        查找元素是否在二叉树中，查找每一个结点，如果查找元素比当前节点小，就在左子树里重新查找，如果查找元素比当前节点大，就在右子树里重新查找

 //查询的方法
    public boolean search(T ele) {
        return searchDG(this.root, ele);
    }

    //语义：从以root为根的二分搜索树中查找元素ele
    private boolean searchDG(Node<T> root, T ele) {
        //递归终止的条件
        if (root == null) {
            return false;
        }
        //递归操作
        if (root.ele.compareTo(ele) == 0) {
            return true;
        } else if (root.ele.compareTo(ele) > 0) {
            return searchDG(root.left, ele);
        } else {
            return searchDG(root.right, ele);
        }
    }

（2）查找最小元素

        二分搜索树中最左边的元素

 //找树中的最小元素
    public T getMinValue() {
        if (this.isEmpty()) {
            return null;
        }
        Optional<Node<T>> optional = getMinNode();
        return optional.get().ele;
    }

//直接查找
private Optional<Node<T>> getMinNode() {
        if (this.root == null) {
            return Optional.empty();
        }
        //一直向左查找
        Node<T> node = this.root;
        while (node.left != null) {
            node = node.left;
        }
        return Optional.of(node);
    }

//利用递归方法查找
    //语义：在以Node为根结点的树中查找最小结点
    private Optional<Node<T>> getMinNode(Node<T> node) {
        if (node.left == null) {
            return Optional.of(node);
        }
        return getMinNode(node.left);
    }

（3）查找最大元素

        二分搜索树中最右边的元素

//找树中的最大元素
    public T getMaxValue() {
        if (this.isEmpty()) {
            return null;
        }
        Optional<Node<T>> optional = getMaxNode(this.root);
        return optional.get().ele;

    }

 //语义：在以Node为根结点的树中查找最大结点
    private Optional<Node<T>> getMaxNode(Node<T> node) {
        if (node.right == null) {
            return Optional.of(node);
        }
        return getMaxNode(node.right);
    }

5.二分搜索树的遍历

树的遍历有四种：前序遍历；中序遍历；后序遍历；层序遍历

（1）前序遍历：

首先打印根节点，然后遍历左子树，最后是右子树

【28,16,13,22,30,29,42】

//前序遍历
    public void preTravel() {
        List<AbstractMap.SimpleEntry<T, Integer>> list = new ArrayList<>();
        preTravelDG(this.root, list);
        String str = list.stream().map(item -> "[" + item.getKey() + ":" + item.getValue() + "]").collect(Collectors.joining("-"));
        System.out.println(str);
    }

 //前序遍历以root为根的树，讲解稿保存在list中
    private void preTravelDG(Node<T> root, List<AbstractMap.SimpleEntry<T, Integer>> list) {
        //递归终止条件
        if (root == null) {
            return;
        }
        //递归操作
        list.add(new AbstractMap.SimpleEntry<>(root.ele, root.frequence));
        //遍历左子树
        preTravelDG(root.left, list);
        //遍历右子树
        preTravelDG(root.right, list);
    }

（2）中序遍历：

先遍历左子树，在打印中间结点，最后遍历右子树

【13,16,22,28,29,30,42】

//中序遍历
    public void midTravel() {
        List<AbstractMap.SimpleEntry<T, Integer>> list = new ArrayList<>();
        midTravelDG(this.root, list);
        String str = list.stream().map(item -> item.toString()).collect(Collectors.joining("-"));
        System.out.println(str);
    }

//中序遍历以root为根的树，讲解稿保存在list中
    private void midTravelDG(Node<T> root, List<AbstractMap.SimpleEntry<T, Integer>> list) {
        //递归终止条件
        if (root == null) {
            return;
        }
        //递归操作
        //遍历左子树
        preTravelDG(root.left, list);
        list.add(new AbstractMap.SimpleEntry<>(root.ele, root.frequence));
        //遍历右子树
        preTravelDG(root.right, list);
    }

（3）后序遍历：

先遍历左子树，在遍历右子树，最后在打印中间结点

【13,22,16,29,42,30,28】

 //后序遍历
    public void sufTravel() {
        List<AbstractMap.SimpleEntry<T, Integer>> list = new ArrayList<>();
        sufTravelDG(this.root, list);
        String str = list.stream().map(item -> item.toString()).collect(Collectors.joining("-"));
        System.out.println(str);
    }

 //后序遍历以root为根的树，讲解稿保存在list中
    private void sufTravelDG(Node<T> root, List<AbstractMap.SimpleEntry<T, Integer>> list) {
        //递归终止条件
        if (root == null) {
            return;
        }
        //递归操作
        //遍历左子树
        preTravelDG(root.left, list);
        //遍历右子树
        preTravelDG(root.right, list);
        list.add(new AbstractMap.SimpleEntry<>(root.ele, root.frequence));
    }

可以看到，先中后序遍历的代码区别只是在递归最后将元素添加到list的位置不同而已

（4）层序遍历：

一层一层的打印

【28,16,30,13,22,29,42】

//层序遍历
    public void levelTravel() {
        //判断树是否为空
        if (this.isEmpty()) {
            return;
        }
        Queue<AbstractMap.SimpleEntry<Node<T>, Integer>> queue = new LinkedList<>();
        //1.先将根结点入队
        queue.add(new AbstractMap.SimpleEntry<>(this.root, 1));
        //2.遍历队列
        while (!queue.isEmpty()) {
            //2-1.出队
            AbstractMap.SimpleEntry<Node<T>, Integer> pair = queue.poll();
            //结点
            Node<T> node = pair.getKey();
            //层
            int level = pair.getValue();
            ;
            System.out.println("[val:" + node.ele + ",level:" + level + "]");
            //2-2.判断左右子树是否为空
            if (node.left != null) {
                queue.add(new AbstractMap.SimpleEntry<>(node.left, level + 1));
            }
            if (node.right != null) {
                queue.add(new AbstractMap.SimpleEntry<>(node.right, level + 1));
            }
        }
    }

6.删除操作

删除的操作中，需要注意删除后二分搜索树也会因此改变，所以要分情况讨论

（1）删除最小元素

删除最小元素并不需要改变树，只需要失去关联关系即可

 //从树中删除最小的结点
    public T removeMinNode() {
        T result = getMinValue();
        if (result == null) {
            return null;
        }
        //更新根结点
        this.root = removeMinNode(this.root);
        return result;
    }

    //语义：从以Node为根的二分搜索树中删除元素最小的结点
    private Node<T> removeMinNode(Node<T> node) {
        //递归终止条件
        if (node.left == null) {
            //删除操作
            //1.记录右子树
            Node<T> rightTree = node.right;
            //失去关联关系
            node.right = null;
            //3.跟新size
            this.size--;
            return rightTree;
        }
        //递归操作
        node.left = removeMinNode(node.left);
        return node;
    }

（2）删除最大元素

跟删除最小元素一样，只需要失去关联关系即可

//从树中删除最大的结点
    public T removeMaxNode() {
        T result = getMaxValue();
        if (result == null) {
            return null;
        }
        //更新根结点
        this.root = removeMaxNode(this.root);
        return result;
    }

    //语义：从以Node为根的二分搜索树中删除元素最大的结点
    private Node<T> removeMaxNode(Node<T> node) {
        //递归终止条件
        if (node.right == null) {
            //删除操作
            //1.记录左子树
            Node<T> leftTree = node.left;
            //失去关联关系
            node.left = null;
            //3.跟新size
            this.size--;
            return leftTree;
        }
        //递归操作
        node.right = removeMaxNode(node.right);
        return node;
    }

（3）删除任意元素

在删除任意元素中，需要考虑删除结点有没有左右子树

//语义：从以Node为根的二分搜索树中删除值为ele的结点
    private Node<T> remove(Node<T> node, T ele) {
        //递归终止的条件
        //没有找到
        if (node == null) {
            return null;
        }
        //找到了
        if (node.ele.compareTo(ele) == 0) {
            this.size--;
            //Node就是要删除的结点
            if (node.left == null) {
                Node<T>rightNode=node.right;
                node.right=null;
                return rightNode;
            } else if (node.right == null) {
                Node<T>leftNode=node.left;
                node.left=null;
                return leftNode;
            } else {
                Node<T> suffixNode = getMinNode(node.right).get();
                suffixNode.right=removeMinNode(node.right);
                suffixNode.left=node.left;
                this.size++;
                //失去关联关系
                node.left=node.right=null;
                return suffixNode;
            }
        }
        //递归操作
        if (node.ele.compareTo(ele) > 0) {
            node.left = remove(node.left, ele);
        } else {
            node.right = remove(node.right, ele);
        }
        return node;
    }

（4）删除根节点

直接删除关联关系即可

 //删除根节点
    public void removeRoot(){
        if(this.root==null){
            return;
        }
        remove(this.root.ele);
    }

四、完整代码

package com.algo.lesson.lesson04;

import java.util.*;
import java.util.stream.Collectors;

//二分搜索树
/*
保存到结点中的元素值必须具有可比性
 */
public class BinearySeachTree<T extends Comparable<T>> {
    //树的结点
    private static class Node<T> {
        private final T ele;//结点的值
        private int frequence;//频率
        private Node<T> left, right;//分别指向左右孩子的索引

        public Node(T ele) {
            this.ele = ele;
            this.left = this.right = null;
        }

    }

    //树对应的属性
    private Node<T> root;//树的根节点
    private int size;//结点的个数

    //构建树
    public BinearySeachTree() {
        this.root = null;
        this.size = 0;
    }

    //获取树中结点的个数
    public int getSize() {
        return this.size;
    }

    //向树中添加结点
    public void add(T ele) {
        //更新根结点
        this.root = addDG(this.root, ele);
    }

    //语义：向以root为根的二分搜索树中添加元素ele
    private Node<T> addDG(Node<T> root, T ele) {
        //递归终止条件
        if (root == null) {
            this.size++;
            return new Node<T>(ele);
        }
        //递归操作
        if (root.ele.compareTo(ele) > 0) {
            root.left = addDG(root.left, ele);
        } else if (root.ele.compareTo(ele) < 0) {
            root.right = addDG(root.right, ele);
        } else {
            //更新频率
            root.frequence++;
        }
        return root;
    }

    //查询的方法
    public boolean search(T ele) {
        return searchDG(this.root, ele);
    }

    //语义：从以root为根的二分搜索树中查找元素ele
    private boolean searchDG(Node<T> root, T ele) {
        //递归终止的条件
        if (root == null) {
            return false;
        }
        //递归操作
        if (root.ele.compareTo(ele) == 0) {
            return true;
        } else if (root.ele.compareTo(ele) > 0) {
            return searchDG(root.left, ele);
        } else {
            return searchDG(root.right, ele);
        }
    }

    //二分搜索树的遍历

    //前序遍历
    public void preTravel() {
        List<AbstractMap.SimpleEntry<T, Integer>> list = new ArrayList<>();
        preTravelDG(this.root, list);
        String str = list.stream().map(item -> "[" + item.getKey() + ":" + item.getValue() + "]").collect(Collectors.joining("-"));
        System.out.println(str);
    }

    //中序遍历
    public void midTravel() {
        List<AbstractMap.SimpleEntry<T, Integer>> list = new ArrayList<>();
        midTravelDG(this.root, list);
        String str = list.stream().map(item -> item.toString()).collect(Collectors.joining("-"));
        System.out.println(str);
    }

    //后序遍历
    public void sufTravel() {
        List<AbstractMap.SimpleEntry<T, Integer>> list = new ArrayList<>();
        sufTravelDG(this.root, list);
        String str = list.stream().map(item -> item.toString()).collect(Collectors.joining("-"));
        System.out.println(str);
    }

    //前序遍历以root为根的树，讲解稿保存在list中
    private void preTravelDG(Node<T> root, List<AbstractMap.SimpleEntry<T, Integer>> list) {
        //递归终止条件
        if (root == null) {
            return;
        }
        //递归操作
        list.add(new AbstractMap.SimpleEntry<>(root.ele, root.frequence));
        //遍历左子树
        preTravelDG(root.left, list);
        //遍历右子树
        preTravelDG(root.right, list);
    }

    //中序遍历以root为根的树，讲解稿保存在list中
    private void midTravelDG(Node<T> root, List<AbstractMap.SimpleEntry<T, Integer>> list) {
        //递归终止条件
        if (root == null) {
            return;
        }
        //递归操作
        //遍历左子树
        preTravelDG(root.left, list);
        list.add(new AbstractMap.SimpleEntry<>(root.ele, root.frequence));
        //遍历右子树
        preTravelDG(root.right, list);
    }

    //后序遍历以root为根的树，讲解稿保存在list中
    private void sufTravelDG(Node<T> root, List<AbstractMap.SimpleEntry<T, Integer>> list) {
        //递归终止条件
        if (root == null) {
            return;
        }
        //递归操作
        //遍历左子树
        preTravelDG(root.left, list);
        //遍历右子树
        preTravelDG(root.right, list);
        list.add(new AbstractMap.SimpleEntry<>(root.ele, root.frequence));
    }

    //判断树是否为空
    public boolean isEmpty() {
        return this.size == 0;
    }

    //层序遍历
    public void levelTravel() {
        //判断树是否为空
        if (this.isEmpty()) {
            return;
        }
        Queue<AbstractMap.SimpleEntry<Node<T>, Integer>> queue = new LinkedList<>();
        //1.先将根结点入队
        queue.add(new AbstractMap.SimpleEntry<>(this.root, 1));
        //2.遍历队列
        while (!queue.isEmpty()) {
            //2-1.出队
            AbstractMap.SimpleEntry<Node<T>, Integer> pair = queue.poll();
            //结点
            Node<T> node = pair.getKey();
            //层
            int level = pair.getValue();
            ;
            System.out.println("[val:" + node.ele + ",level:" + level + "]");
            //2-2.判断左右子树是否为空
            if (node.left != null) {
                queue.add(new AbstractMap.SimpleEntry<>(node.left, level + 1));
            }
            if (node.right != null) {
                queue.add(new AbstractMap.SimpleEntry<>(node.right, level + 1));
            }
        }
    }

    //找树中的最小元素
    public T getMinValue() {
        if (this.isEmpty()) {
            return null;
        }
        Optional<Node<T>> optional = getMinNode();
        return optional.get().ele;
    }

    //找树中的最大元素
    public T getMaxValue() {
        if (this.isEmpty()) {
            return null;
        }
        Optional<Node<T>> optional = getMaxNode(this.root);
        return optional.get().ele;

    }

    private Optional<Node<T>> getMinNode() {
        if (this.root == null) {
            return Optional.empty();
        }
        //一直向左查找
        Node<T> node = this.root;
        while (node.left != null) {
            node = node.left;
        }
        return Optional.of(node);
    }

    //递归
    //语义：在以Node为根结点的树中查找最小结点
    private Optional<Node<T>> getMinNode(Node<T> node) {
        if (node.left == null) {
            return Optional.of(node);
        }
        return getMinNode(node.left);
    }

    //语义：在以Node为根结点的树中查找最大结点
    private Optional<Node<T>> getMaxNode(Node<T> node) {
        if (node.right == null) {
            return Optional.of(node);
        }
        return getMaxNode(node.right);
    }

    //删除操作
    //从树中删除最小的结点
    public T removeMinNode() {
        T result = getMinValue();
        if (result == null) {
            return null;
        }
        //更新根结点
        this.root = removeMinNode(this.root);
        return result;
    }

    //语义：从以Node为根的二分搜索树中删除元素最小的结点
    private Node<T> removeMinNode(Node<T> node) {
        //递归终止条件
        if (node.left == null) {
            //删除操作
            //1.记录右子树
            Node<T> rightTree = node.right;
            //失去关联关系
            node.right = null;
            //3.跟新size
            this.size--;
            return rightTree;
        }
        //递归操作
        node.left = removeMinNode(node.left);
        return node;
    }

    //删除操作
    //从树中删除最大的结点
    public T removeMaxNode() {
        T result = getMaxValue();
        if (result == null) {
            return null;
        }
        //更新根结点
        this.root = removeMaxNode(this.root);
        return result;
    }

    //语义：从以Node为根的二分搜索树中删除元素最大的结点
    private Node<T> removeMaxNode(Node<T> node) {
        //递归终止条件
        if (node.right == null) {
            //删除操作
            //1.记录左子树
            Node<T> leftTree = node.left;
            //失去关联关系
            node.left = null;
            //3.跟新size
            this.size--;
            return leftTree;
        }
        //递归操作
        node.right = removeMaxNode(node.right);
        return node;
    }

    //删除任意结点
    public void remove(T ele) {
        //根据值查找结点
        this.root = remove(this.root, ele);
    }

    //语义：从以Node为根的二分搜索树中删除值为ele的结点
    private Node<T> remove(Node<T> node, T ele) {
        //递归终止的条件
        //没有找到
        if (node == null) {
            return null;
        }
        //找到了
        if (node.ele.compareTo(ele) == 0) {
            this.size--;
            //Node就是要删除的结点
            if (node.left == null) {
                Node<T>rightNode=node.right;
                node.right=null;
                return rightNode;
            } else if (node.right == null) {
                Node<T>leftNode=node.left;
                node.left=null;
                return leftNode;
            } else {
                Node<T> suffixNode = getMinNode(node.right).get();
                suffixNode.right=removeMinNode(node.right);
                suffixNode.left=node.left;
                this.size++;
                //失去关联关系
                node.left=node.right=null;
                return suffixNode;
            }
        }
        //递归操作
        if (node.ele.compareTo(ele) > 0) {
            node.left = remove(node.left, ele);
        } else {
            node.right = remove(node.right, ele);
        }
        return node;
    }

    //删除根节点
    public void removeRoot(){
        if(this.root==null){
            return;
        }
        remove(this.root.ele);
    }

}

五、例题

1.700. 二叉搜索树中的搜索

​​​​

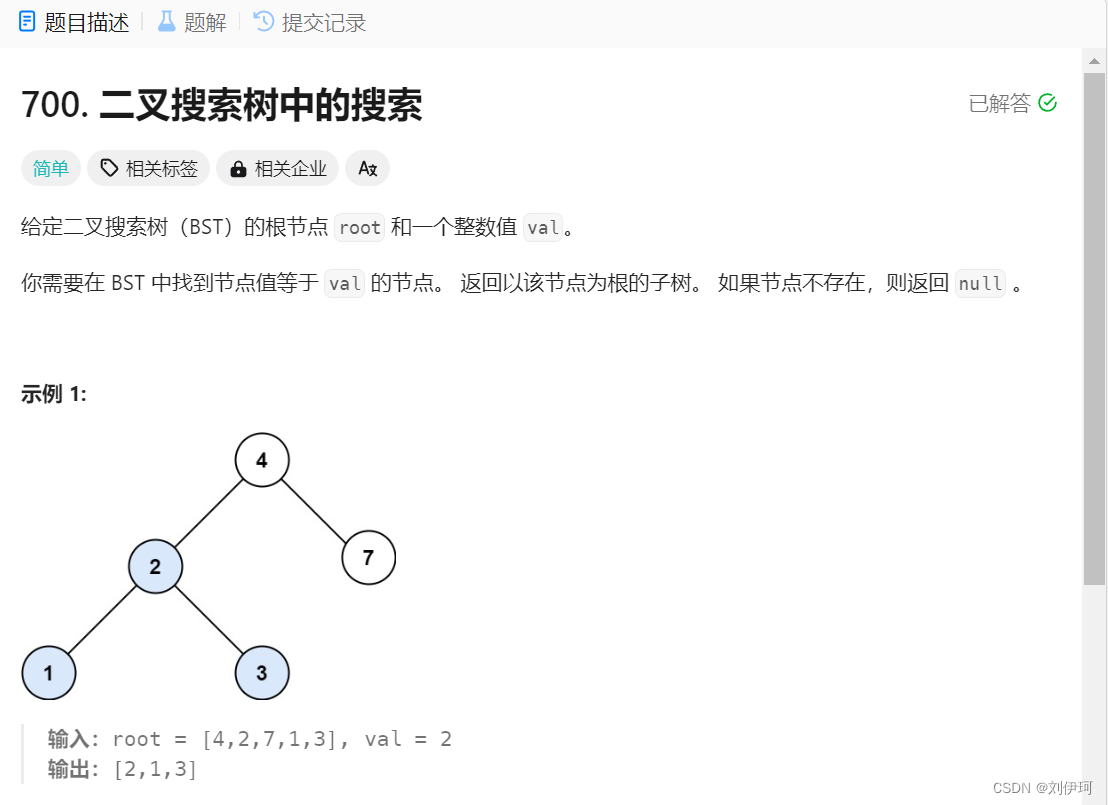
class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if(root==null){
            return null;
        }
        if(val==root.val){
            return root;
        }
        return searchBST(val<root.val?root.left:root.right,val);
    }
}

2.力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

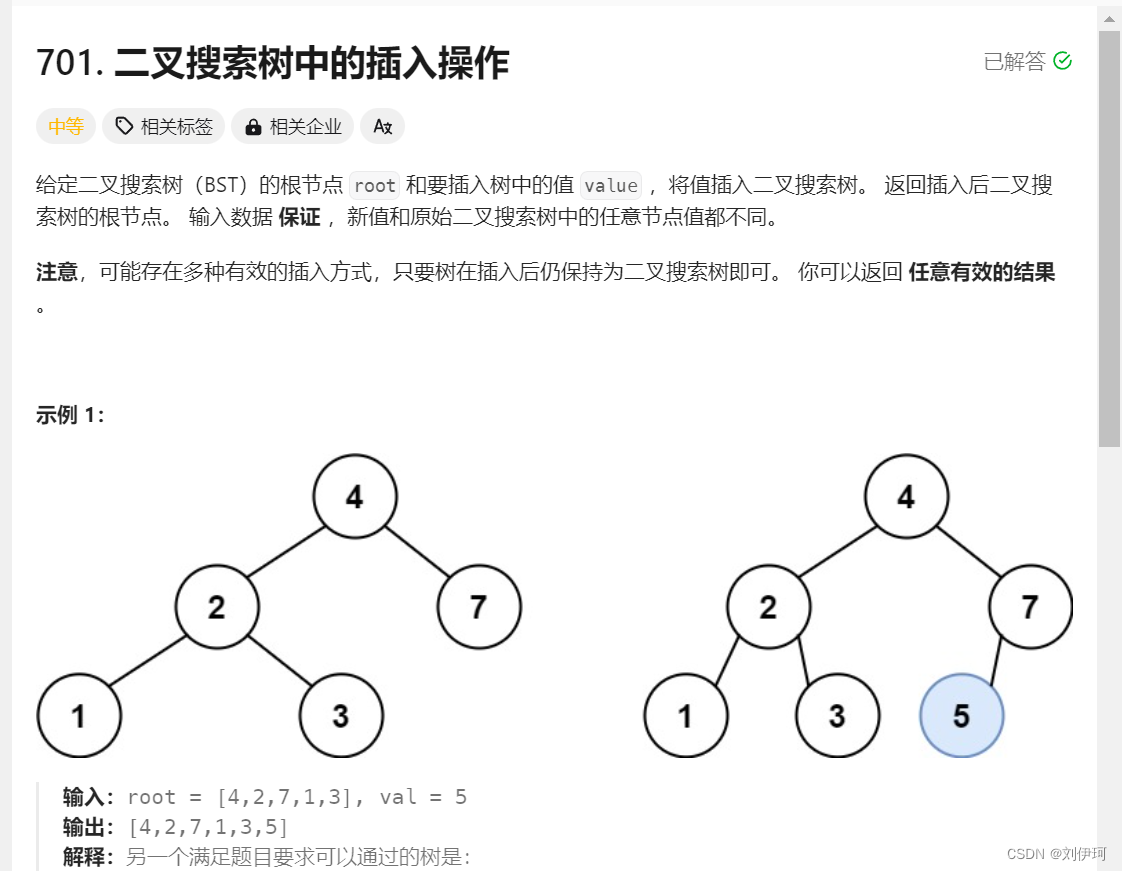
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
//更新根结点
        return root = addDG(root, val);
    }

    //语义：向以root为根的二分搜索树中添加元素ele
    private TreeNode addDG(TreeNode root, int val) {
        //递归终止条件
        if (root == null) {
            return new TreeNode(val);
        }
        //递归操作
        if (root.val>val) {
            root.left = addDG(root.left, val);
        } else if (root.val<val) {
            root.right = addDG(root.right, val);
        }
        return root;
    }
}

3.力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

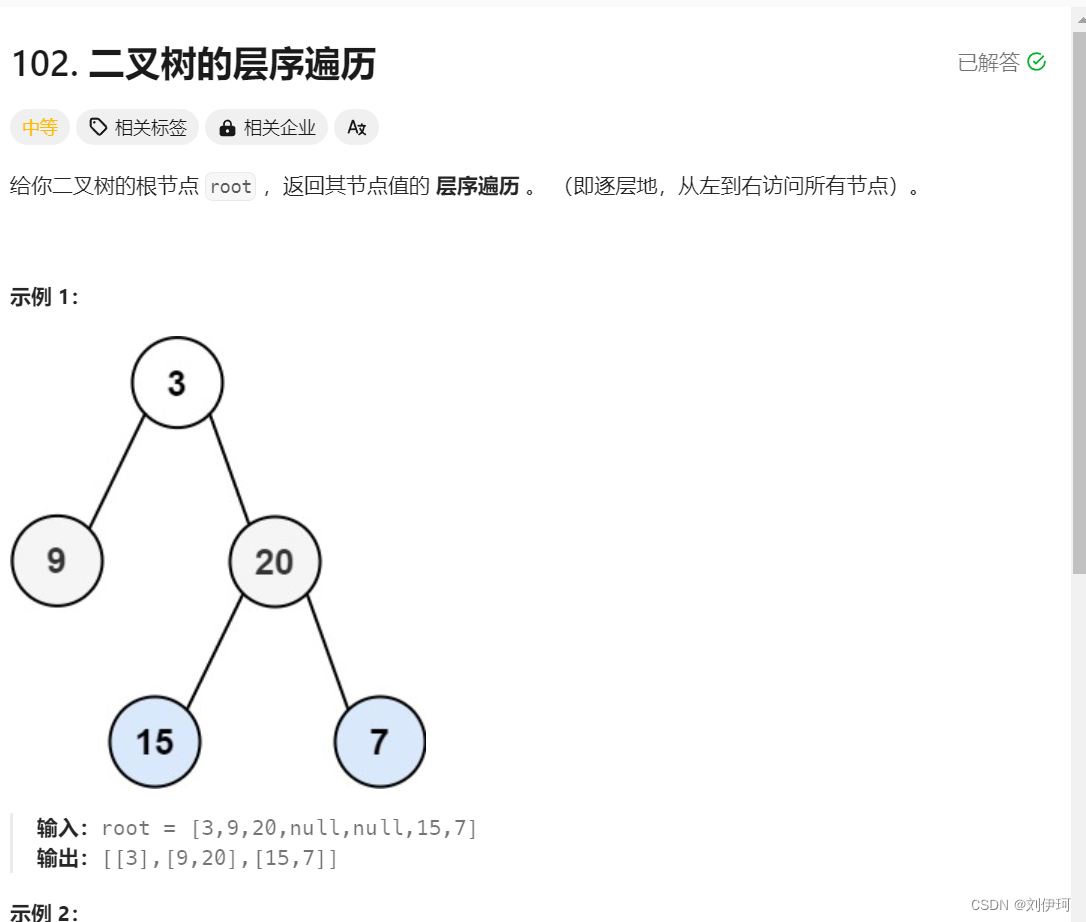
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> list = new ArrayList<List<Integer>>();
        if (root == null) {
            return list;
        }
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            List<Integer> level = new ArrayList<Integer>();
            int temp = queue.size();
            for (int i = 1; i <= temp; i++) {
                TreeNode node = queue.poll();
                level.add(node.val);
                if (node.left != null) {
                    queue.offer(node.left);
                }
                if (node.right != null) {
                    queue.offer(node.right);
                }
            }
            list.add(level);
        }
        return list;
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1419277.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

数字美妆技术：美颜SDK和动态贴纸技术的崭新时代

数字美妆技术：美颜SDK和动态贴纸技术的崭新时代

数字美妆的兴起标志着人们对于自身形象的追求不再局限于现实生活&#xff0c;而是延伸到了虚拟世界。同时&#xff0c;美颜SDK的动态贴纸技术也开始进入到大家的视野之中。 一、美颜SDK&#xff1a;技术之作 通过复杂的图像处理算法&#xff0c;美颜SDK能够实时检测人脸&…
阅读更多...
Lua语法基本使用

Lua语法基本使用

&#x1f353; 简介&#xff1a;java系列技术分享(&#x1f449;持续更新中…&#x1f525;) &#x1f353; 初衷:一起学习、一起进步、坚持不懈 &#x1f353; 如果文章内容有误与您的想法不一致,欢迎大家在评论区指正&#x1f64f; &#x1f353; 希望这篇文章对你有所帮助,欢…
阅读更多...
【网络基础】IP

【网络基础】IP

IP协议报头 4位版本号(version): 指定IP协议的版本, 对于IPv4来说, 就是4.4位头部长度(header length): IP头部的长度是多少个32bit, 也就是 length * 4 的字节数. 4bit表示最大的数字是15, 因此IP头部最大长度是60字节. 8位服务类型(Type Of Service): 3位优先权字段(已经弃用…
阅读更多...
网络空间搜索引擎

网络空间搜索引擎

随着互联网、物联网、传感网、社交网络等信息系统所构成的泛在网络不断 发展&#xff0c;网络终端设备数量呈指数级上升。这为企业进行终端设备资产清点和统一 管控带来了巨大挑战&#xff0c;同时也引发了一系列安全问题&#xff0c;网络攻击与防御的博弈从 单边代码漏洞发展到…
阅读更多...
SpringMVC 自动配置

SpringMVC 自动配置

SpringMVC 自动配置 一、WebMvcAutoConfiguration&#xff08;SpringMVC自动配置&#xff09;二、DisPatcherServletAutoConfiguration.class&#xff08;中央调度器自动配置&#xff09;三、WebMvcConfigurationSupport&#xff08;SpringMVC组件配置类&#xff09;四、Servle…
阅读更多...
RHCE 搭建DNS域名解析服务器

RHCE 搭建DNS域名解析服务器

目录 一、前述 1、BIND&#xff08;Berkeley Internet Name Domain&#xff09; 2、bind服务中三个关键文件 1&#xff09;主配置文件/etc/named.conf 2&#xff09;区域配置文件/etc/named.rfc1912.zones 正向解析 反向解析 3&#xff09;数据配置文件目录/var/named/…
阅读更多...
STM32 1-5

STM32 1-5

目录 STM32简介 点亮PC13LED GPIO LED闪烁 LED流水灯 按键控制LED 光敏传感器控制蜂鸣器 OLED调试工具 OLED显示 EXTI外部中断 对射式红外传感器计次 旋转编码器计次 继续 STM32简介 点亮PC13LED main.c #include "stm32f10x.h" // D…
阅读更多...
Hadoop-MapReduce-YarnChild启动篇

Hadoop-MapReduce-YarnChild启动篇

一、源码下载 下面是hadoop官方源码下载地址&#xff0c;我下载的是hadoop-3.2.4&#xff0c;那就一起来看下吧 Index of /dist/hadoop/core 二、上下文 在上一篇<Hadoop-MapReduce-MRAppMaster启动篇>中已经将到&#xff1a;MRAppMaster的启动&#xff0c;那么运行M…
阅读更多...
如何让wordpress首页只显示某一篇文章全部内容？在您的主页显示选择

如何让wordpress首页只显示某一篇文章全部内容？在您的主页显示选择

大多数WordPress站点首页默认都是显示最新发布的文章列表&#xff0c;不过有些站点比较特殊&#xff0c;只想显示某一篇文章的全部内容&#xff0c;那么应该怎么设置呢&#xff1f; 其实&#xff0c;WordPress后台 >> 设置 >> 阅读 >> 在“您的主页显示”中…
阅读更多...
VS+QT 配置Eigen库

VS+QT 配置Eigen库

1、下载Eigen库&#xff0c;如下&#xff1a; 2、解压到项目目录下&#xff0c;如下&#xff1a; 3、 在C/C中包含文件&#xff0c;如下&#xff1a; 4、在头文件中加入如下代码&#xff1a; 5、测试代码&#xff1a; //.cpp文件 #include "testEigen.h"testEigen::…
阅读更多...
【Python】03快速上手爬虫案例三：搞定药师帮

【Python】03快速上手爬虫案例三：搞定药师帮

文章目录 前言1、破解验证码2、获取数据 前言 流程&#xff1a;通过用户名、密码、搞定验证码&#xff0c;登录进药师帮网站&#xff0c;然后抓取想要的数据。 爬取数据&#xff0c;最终效果图&#xff1a; 1、破解验证码 使用药师帮测试系统&#xff1a;https://dianrc.ysb…
阅读更多...
快速入门存内计算—助力人工智能加速深度学习模型的训练和推理

快速入门存内计算—助力人工智能加速深度学习模型的训练和推理

存内计算&#xff1a;提高计算性能和能效的新技术 传统的计算机架构是将数据存储在存储器中&#xff0c;然后将数据传输到计算单元进行处理。这种架构存在一个性能瓶颈&#xff0c;即数据传输延迟。存内计算通过将计算单元集成到存储器中&#xff0c;消除了数据传输延迟&#…
阅读更多...
HiveSQL题——窗口函数(lag/lead)

HiveSQL题——窗口函数(lag/lead)

目录 一、窗口函数的知识点 1.1 窗户函数的定义 1.2 窗户函数的语法 1.3 窗口函数分类 1.4 前后函数:lag/lead 二、实际案例 2.1 股票的波峰波谷 0 问题描述 1 数据准备 2 数据分析 3 小结 2.2 前后列转换&#xff08;面试题&#xff09; 0 问题描述 1 数据准备 …
阅读更多...
kubernetes-快速部署一套k8s集群

kubernetes-快速部署一套k8s集群

1、前置知识点 1.1 生产环境可部署Kubernetes集群的两种方式 目前生产部署Kubernetes集群主要有两种方式&#xff1a; kubeadm Kubeadm是一个K8s部署工具&#xff0c;提供kubeadm init和kubeadm join&#xff0c;用于快速部署Kubernetes集群。 二进制包 从github下载发行…
阅读更多...
04.对象树

04.对象树

一、引入 1.QT实现输出"hello world" 使用QT编写"hello world"程序&#xff0c;有两种实现方式&#xff1a; &#xff08;1&#xff09;直接在生成的ui文件中&#xff0c;拖入一个label控件&#xff0c;双击控件编辑内容即可实现 &#xff08;2&#xff0…
阅读更多...
【C++历练之路】探秘C++三大利器之一——多态

【C++历练之路】探秘C++三大利器之一——多态

W...Y的主页 &#x1f60a; 代码仓库分享&#x1f495; 前言&#x1f354;: 在计算机科学的广袤领域中&#xff0c;C多态性是一门令人着迷的技术艺术&#xff0c;它赋予我们的代码更强大的灵活性和可维护性。想象一下&#xff0c;你正在构建一个程序&#xff0c;需要适应不断…
阅读更多...
【技术分享】远程透传网关-单网口快速实现威纶通触摸屏程序远程上下载

【技术分享】远程透传网关-单网口快速实现威纶通触摸屏程序远程上下载

准备工作 一台可联网操作的电脑一台单网口的远程透传网关及博达远程透传配置工具网线一条&#xff0c;用于实现网络连接和连接触摸屏一台威纶通触摸屏及其编程软件一张4G卡或WIFI天线实现通讯(使用4G联网则插入4G SIM卡&#xff0c;WIFI联网则将WIFI天线插入USB口&#xff09;…
阅读更多...
Redis 面试题 | 19.精选Redis高频面试题

Redis 面试题 | 19.精选Redis高频面试题

&#x1f90d; 前端开发工程师、技术日更博主、已过CET6 &#x1f368; 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 &#x1f560; 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 &#x1f35a; 蓝桥云课签约作者、上架课程《Vue.js 和 E…
阅读更多...
Mac安装及配置MySql及图形化工具MySQLworkbench安装

Mac安装及配置MySql及图形化工具MySQLworkbench安装

Mac下载配置MySql mysql下载及安装 下载地址&#xff1a;https://dev.mysql.com/downloads/mysql/ 根据自己电脑确定下载x86还是ARM版本的 如果不确定&#xff0c;可以查看自己电脑版本&#xff0c;终端输入命令 uname -a 点击Download下载&#xff0c;可跳过登录注册&…
阅读更多...
沙龙回顾｜“强标”发布在即，汽车数据安全的挑战与应对

沙龙回顾｜“强标”发布在即，汽车数据安全的挑战与应对

随着智能汽车产业驶入发展快车道&#xff0c;“数据安全”的重要性也日益突出。2020年以来发现的针对整车企业、车联网信息服务提供商等相关企业的恶意攻击达到280余万次。2023年初至今&#xff0c;就发生超过20起与车企相关数据泄露事件&#xff0c;汽车数据安全的现状不容乐观…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023