Vojtěch Jarník
一、Prim算法简史
Prim算法(普里姆算法),是1930年捷克数学家算法沃伊捷赫·亚尔尼克(Vojtěch Jarník)最早设计;
1957年,由美国计算机科学家罗伯特·普里姆独立实现;
1959年,艾兹格·迪科斯彻再次发现了该算法。
二、Prim算法思路
将点分为两拨,(1)已经加入最小生成树的和(2)未加入的。找到未加入中距离集合最近的点,添加该点,修改其它点到集合的距离。直到所有结点都加入到最小生成树。Prim算法与Dijkstra算法都是贪心算法,适用于稠密图,时间复杂度都是O(V^2);也可以进行优化,其时间复杂度与边数无关。
三、Prim算法描述
(1)以某一个点A开始,将此点加入集合U,并访问其所有经过此点的边。
(2)在这些边寻找权重最小的边,并且要求它的另一个点B没有被访问过。如果 能找到,就将点B加入集合U。接着我们要访问,所有经过点A或点B的边。
(3)重复2的过程,直到所有的点都加入U。
(4)此时由所有边构成的树即为最小生成树。
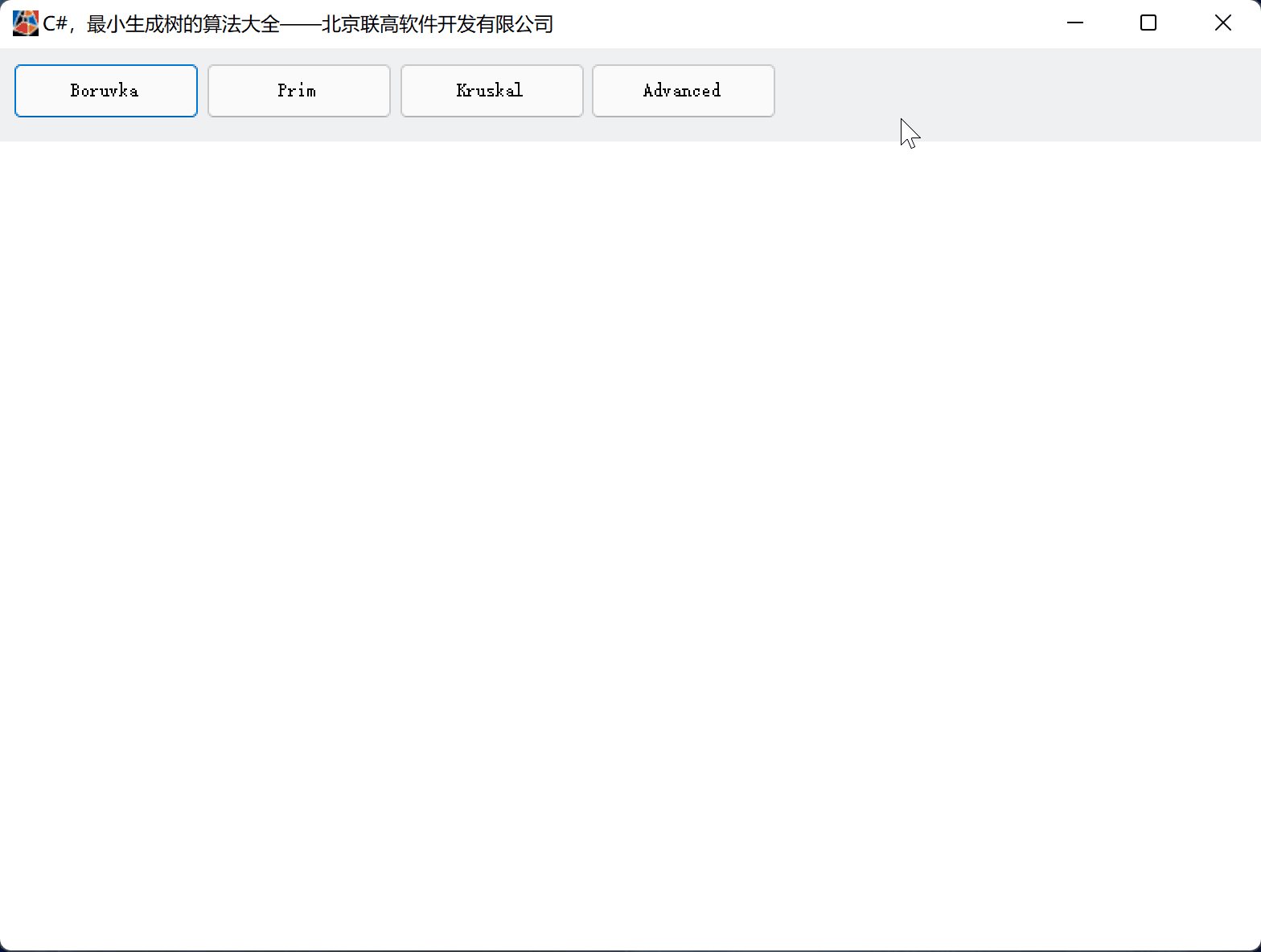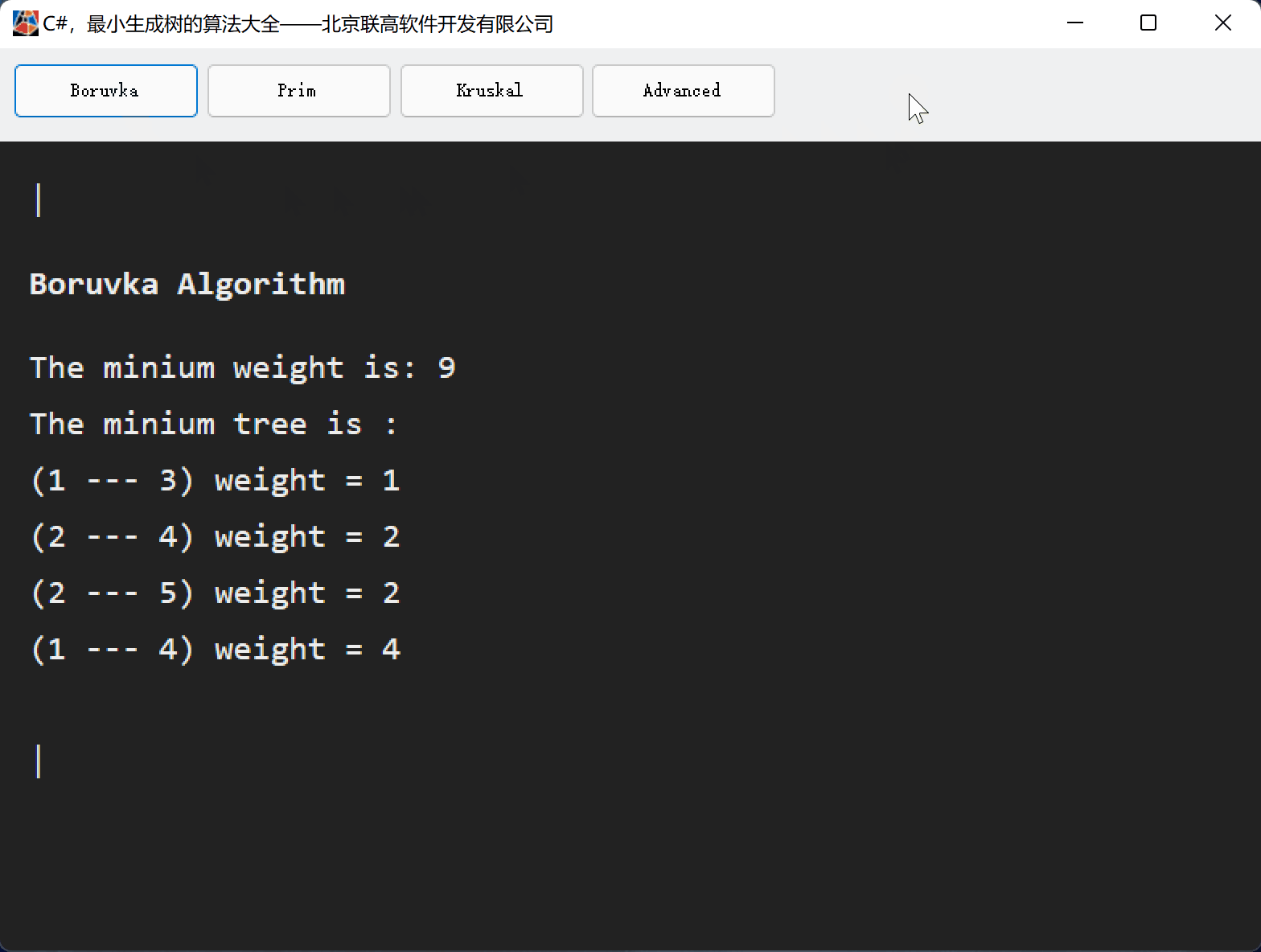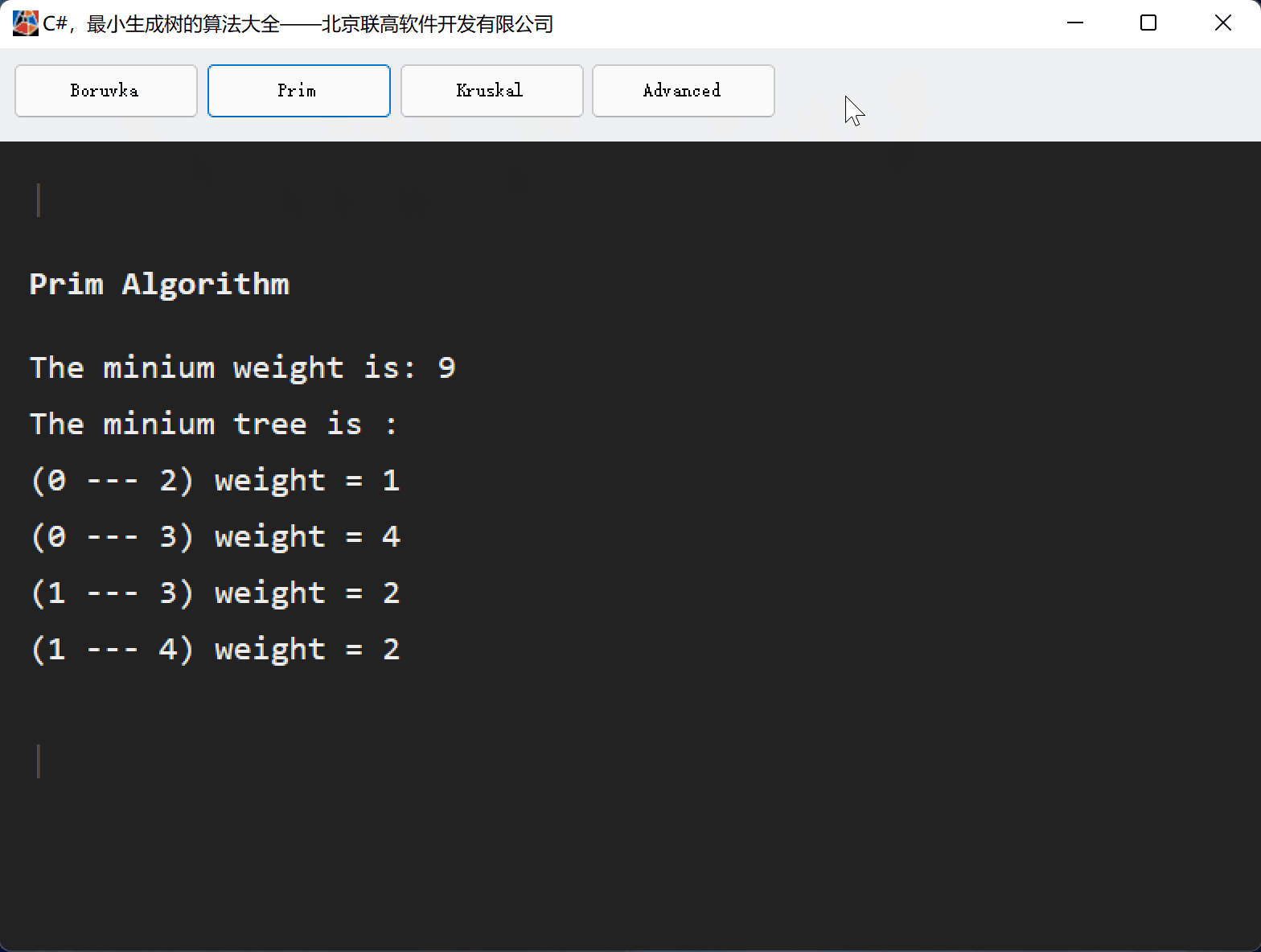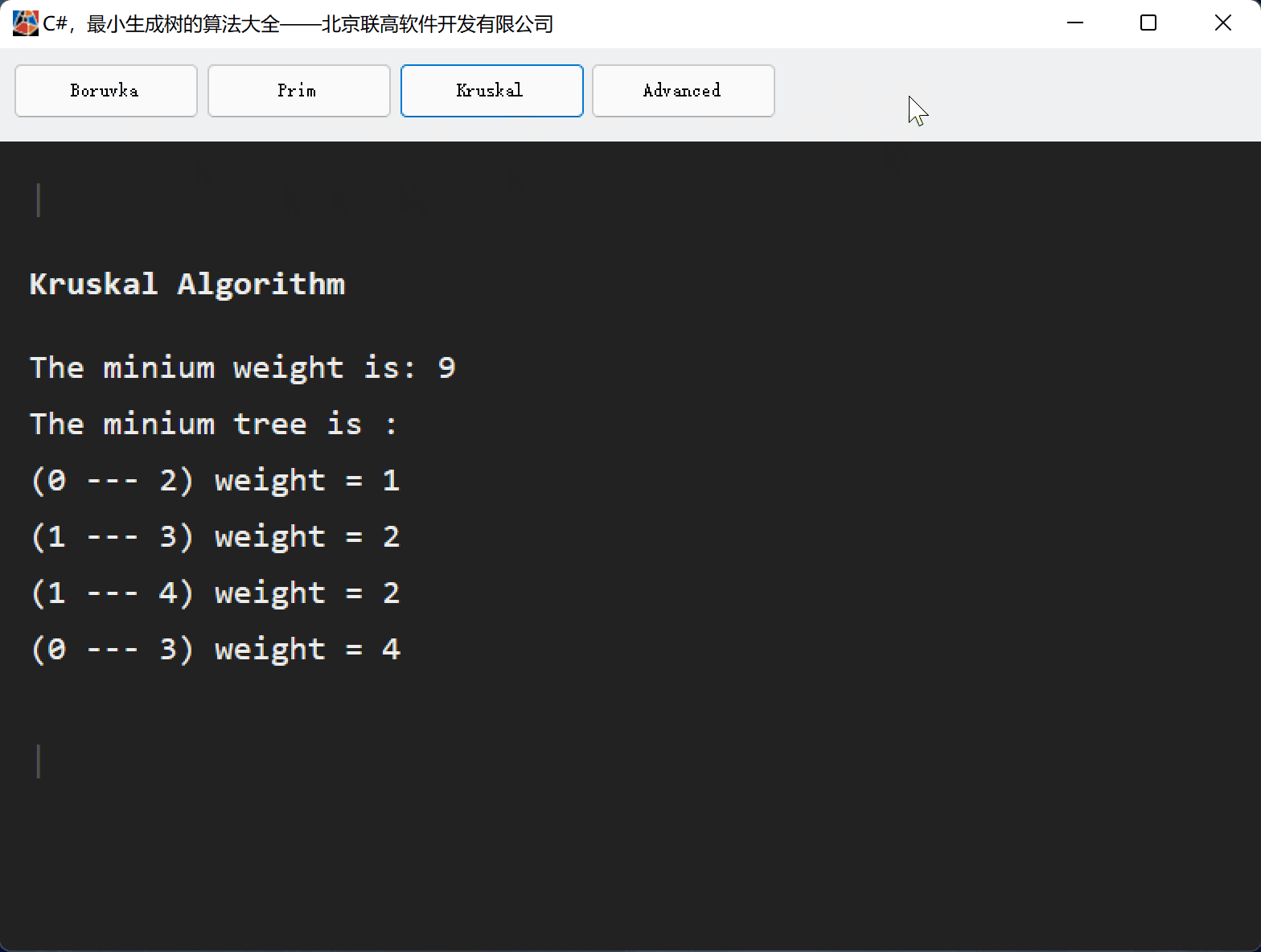
四、Prim算法源代码
核心代码部分:
1 文本格式
using System;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
/// <summary>
/// Prim 算法(邻接矩阵表示的简单实现)
/// </summary>
public class MST_Prim_Algorithm
{
private static bool IsValidEdge(int u, int v, bool[] inMST)
{
if (u == v)
{
return false;
}
if (inMST[u] == false && inMST[v] == false)
{
return false;
}
else if (inMST[u] == true && inMST[v] == true)
{
return false;
}
return true;
}
public static int Execute(Undirected_Graph graph, out List<WeightEdge> tree)
{
tree = new List<WeightEdge>();
int V = graph.Vertex_Number;
int[,] Cost = graph.To_Adjacency_Matrix();
bool[] inMST = new bool[V];
inMST[0] = true;
int edge_count = 0;
int mincost = 0;
while (edge_count < V - 1)
{
int min = Int32.MaxValue;
int a = -1;
int b = -1;
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
if (Cost[i, j] < min)
{
if (IsValidEdge(i, j, inMST))
{
min = Cost[i, j];
a = i;
b = j;
}
}
}
}
if (a != -1 && b != -1)
{
tree.Add(new WeightEdge(a,b,min));
edge_count++;
mincost = mincost + min;
inMST[b] = inMST[a] = true;
}
}
return mincost;
}
}
}
2 代码格式
using System;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
/// <summary>
/// Prim 算法(邻接矩阵表示的简单实现)
/// </summary>
public class MST_Prim_Algorithm
{
private static bool IsValidEdge(int u, int v, bool[] inMST)
{
if (u == v)
{
return false;
}
if (inMST[u] == false && inMST[v] == false)
{
return false;
}
else if (inMST[u] == true && inMST[v] == true)
{
return false;
}
return true;
}
public static int Execute(Undirected_Graph graph, out List<WeightEdge> tree)
{
tree = new List<WeightEdge>();
int V = graph.Vertex_Number;
int[,] Cost = graph.To_Adjacency_Matrix();
bool[] inMST = new bool[V];
inMST[0] = true;
int edge_count = 0;
int mincost = 0;
while (edge_count < V - 1)
{
int min = Int32.MaxValue;
int a = -1;
int b = -1;
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
if (Cost[i, j] < min)
{
if (IsValidEdge(i, j, inMST))
{
min = Cost[i, j];
a = i;
b = j;
}
}
}
}
if (a != -1 && b != -1)
{
tree.Add(new WeightEdge(a,b,min));
edge_count++;
mincost = mincost + min;
inMST[b] = inMST[a] = true;
}
}
return mincost;
}
}
}
——————————————————————
POWER BY 315SOFT.COM &
TRUFFER.CN