【代码随想录】刷题笔记Day53

news2025/11/4 10:16:58

前言

不用开组会的我是多么阳光开朗，这周就要离开杭州回家啦，多刷题刷题

115. 不同的子序列 - 力扣（LeetCode）

dp[i][j]
- 以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]
递推公式
- dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
初始化
- dp[i][0] = 1，dp[0][j] = 0，dp[0][0] = 1，遍历从上到下，从左到右

class Solution {
public:
    int numDistinct(string s, string t) {
        vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1));
        for (int i = 0; i < s.size(); i++) dp[i][0] = 1;
        for (int j = 1; j < t.size(); j++) dp[0][j] = 0;
        for (int i = 1; i <= s.size(); i++) {
            for (int j = 1; j <= t.size(); j++) {
                if (s[i - 1] == t[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[s.size()][t.size()];
    }
};

583. 两个字符串的删除操作 - 力扣（LeetCode）

思路一

求最长公共子序列，再求每个串相减所需要的步数，相加

class Solution {
public:
    int minDistance(string word1, string word2) {
        // 求最长公共子序列（不连续）
        int len1 = word1.size();
        int len2 = word2.size();
        int maxlen = 0;
        vector<vector<int>> dp (len1 + 1, vector<int>(len2 + 1, 0));
        for (int i = 1; i <= len1; i++) {
            for (int j = 1; j <= len2; j++) {
                if(word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                maxlen = max(dp[i][j], maxlen);
            }
        }
        // 求每个串减去公共子序列需要的步数，相加
        return len1 + len2 - 2 * maxlen;
    }
};

思路二
- 编辑子串思路，两个字符串都可以进行删除操作
- dp[i][j]含义
  - 以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，达到相等所需要删除元素的最少次数
- 递推公式
  - 当word1[i - 1] 与 word2[j - 1]相同的时候，dp[i][j] = dp[i - 1][j - 1];
  - 当word1[i - 1] 与 word2[j - 1]不相同的时候
    - 情况一：删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1
    - 情况二：删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1
    - 情况三：同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2
    - dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
    - 可简化为dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
- 初始化
  - 空字符串要全删，dp[i][0] = i，dp[0][j] = j，从上到下从左到右
- ```
class Solution {
public:
    int minDistance(string word1, string word2) {
        int len1 = word1.size();
        int len2 = word2.size();
        vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1));
        for(int i = 0; i <= len1; i++) dp[i][0] = i;
        for(int j = 0; j <= len2; j++) dp[0][j] = j;
        for(int i = 1; i <= len1; i++){
            for(int j = 1; j <= len2; j++){
                if(word1[i-1] == word2[j-1]){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    dp[i][j] = min(dp[i-1][j] + 1, dp[i][j-1] + 1);
                }
            }
        }
        return dp[len1][len2];
    }
};
```

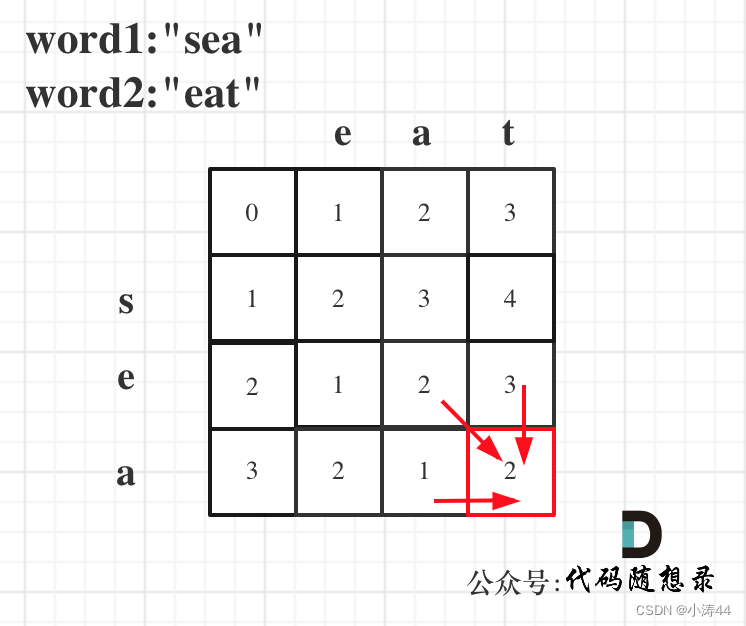
72. 编辑距离 - 力扣（LeetCode）

终极经典题目，暴力都没思路，1→2增删改，实际上是1→3←2删改
dp[i][j]含义
- 以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离（最小编辑次数）为dp[i][j]

递推公式

if(word1[i-1] == word2[j-1]){
    // 不操作
    dp[i][j] = dp[i-1][j-1];
}else{
    // 增/删：dp[i-1][j] + 1, dp[i][j-1] + 1
    // 改：dp[i-1][j-1] + 1
    dp[i][j] = min(min(dp[i-1][j] + 1, dp[i][j-1] + 1), dp[i-1][j-1] + 1);
}

初始化
- 空字符串要全删，dp[i][0] = i，dp[0][j] = j，从上到下从左到右

class Solution {
public:
    int minDistance(string word1, string word2) {
        int len1 = word1.size();
        int len2 = word2.size();
        vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1));
        for(int i = 0; i <= len1; i++) dp[i][0] = i;
        for(int j = 0; j <= len2; j++) dp[0][j] = j;
        for(int i = 1; i <= len1; i++){
            for(int j = 1; j <= len2; j++){
                if(word1[i-1] == word2[j-1]){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    dp[i][j] = min(min(dp[i-1][j] + 1, dp[i][j-1] + 1), dp[i-1][j-1] + 1);
                }
            }
        }
        return dp[len1][len2];
    }
};