这次作业相对于作业5会麻烦一点点,而且框架相较于作业五的也麻烦了一点,当然作业的难点其实主要还是在扩展作业SAH那块。
目录
- 课程总结与理解(光线追踪)
- 框架梳理
- 作业一:光线生成
- 作业二:光线-三角形相交
- 作业三:包围盒与光线相交
- 作业四:使用BVH求交
- 扩展:使用SAH规则构建BVH,从而加速BVH求交
- 最终效果
- 感悟
- 参考链接
课程总结与理解(光线追踪)
光线追踪流程,从全局来看就是先往scene里面添加物体(包括物体本身的材质信息和各种属性)和光源,其中物体既可以是显示表示(三角网格),也可以是隐式表示(球,用方程)。添加完之后就调用Render函数进行渲染。以上就是对应图形学两个环节,建模和渲染,如果要让他们动起来的话就是还要加个模拟。
渲染流程大概就是先生成光线(视点与屏幕像素中心点的连线),然后光线与场景相交找到第一个与之相交的点,这里就用到了包围盒的思想,加速求交过程,涉及到三个部分,如何构建包围盒(左下角和右上角,与三个轴平行的包围盒),如何计算包围盒与光线求交(和裁剪那边有点类似,本质上就是相似三角形构造比例),以及如何使用包围盒:均匀网格,空间划分,物体划分(BAH)—其中物体划分的规则涉及到了NAIVE规则和SAH规则。当光线与包围盒求交判断有交点之后,就继续与其子包围盒求交,直到找到最后的子包围盒(树的叶子节点),然后让直线与在该叶子节点对应的子包围盒中的全部物体求交,找到最近交点(其中,对于不同物体的求交方法是不一样的,比如对于球这种隐式表示的,就用解析解的方法直接求交点,对于三角网格这种显示表示的,就依次遍历其所有三角形,用线和三角形求交的方法求交点)。之后根据各种渲染的方法对该点着色(不同材质的着色方法不一样,代码里面写了三种材质,对应三种不同的着色方法,并且这里还需要判断点是否处在阴影中,若在阴影中,则不需要着色),然后该点的颜色就会最终返回,作为最终渲染图像的一个像素值。射出全部光线就能得到全部像素值,最终得到渲染图像。
框架梳理
上次作业5由于框架比较好理解,所以没有去理框架,这次为了方便后面作业,就简单理一理。
首先看main函数,总的来看就两个部分,添加模型和光源,然后渲染场景。
int main(int argc, char** argv)
{
Scene scene(1280, 960);
MeshTriangle bunny("../models/bunny/bunny.obj");
scene.Add(&bunny);
scene.Add(std::make_unique<Light>(Vector3f(-20, 70, 20), 1));
scene.Add(std::make_unique<Light>(Vector3f(20, 70, 20), 1));
scene.buildBVH();
Renderer r;
auto start = std::chrono::system_clock::now();
r.Render(scene);
auto stop = std::chrono::system_clock::now();
std::cout << "Render complete: \n";
std::cout << "Time taken: " << std::chrono::duration_cast<std::chrono::hours>(stop - start).count() << " hours\n";
std::cout << " : " << std::chrono::duration_cast<std::chrono::minutes>(stop - start).count() << " minutes\n";
std::cout << " : " << std::chrono::duration_cast<std::chrono::seconds>(stop - start).count() << " seconds\n";
return 0;
}
然后进入Render函数,总的来看就是很简单的生成光线,然后通过castRay函数求出该光线射出去计算得到并最终返回给像素的颜色,得到所有像素颜色之后就能得到最终的渲染图像。
void Renderer::Render(const Scene& scene)
{
std::vector<Vector3f> framebuffer(scene.width * scene.height);
float scale = tan(deg2rad(scene.fov * 0.5));
float imageAspectRatio = scene.width / (float)scene.height;
Vector3f eye_pos(-1, 5, 10);
int m = 0;
for (uint32_t j = 0; j < scene.height; ++j) {
for (uint32_t i = 0; i < scene.width; ++i) {
// generate primary ray direction
float x = (2 * (i + 0.5) / (float)scene.width - 1) *
imageAspectRatio * scale;
float y = (1 - 2 * (j + 0.5) / (float)scene.height) * scale;
// TODO: Find the x and y positions of the current pixel to get the
// direction
// vector that passes through it.
// Also, don't forget to multiply both of them with the variable
// *scale*, and x (horizontal) variable with the *imageAspectRatio*
// Don't forget to normalize this direction!
Vector3f dir = Vector3f(x, y, -1); // Don't forget to normalize this direction!
dir = normalize(dir);
Ray ray = Ray(eye_pos, dir);
framebuffer[m++] = scene.castRay(ray, 0);
}
UpdateProgress(j / (float)scene.height);
}
UpdateProgress(1.f);
// save framebuffer to file
FILE* fp = fopen("binary.ppm", "wb");
(void)fprintf(fp, "P6\n%d %d\n255\n", scene.width, scene.height);
for (auto i = 0; i < scene.height * scene.width; ++i) {
static unsigned char color[3];
color[0] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].x));
color[1] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].y));
color[2] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].z));
fwrite(color, 1, 3, fp);
}
fclose(fp);
}
然后进入castRay函数,这个函数也不难,就通过intersect函数求出光线与场景物体的最近交点,然后就根据不同的材质使用不同的着色方法对该点着色即可。
着色的细节可以参考https://blog.csdn.net/qq_41835314/article/details/124969379,这里不重点阐述这部分,主要重点阐述如何得到这个交点。
Vector3f Scene::castRay(const Ray &ray, int depth) const
{
if (depth > this->maxDepth) {
return Vector3f(0.0,0.0,0.0);
}
Intersection intersection = Scene::intersect(ray);
Material *m = intersection.m;
Object *hitObject = intersection.obj;
Vector3f hitColor = this->backgroundColor;
// float tnear = kInfinity;
Vector2f uv;
uint32_t index = 0;
if(intersection.happened) {
Vector3f hitPoint = intersection.coords;
Vector3f N = intersection.normal; // normal
Vector2f st; // st coordinates
hitObject->getSurfaceProperties(hitPoint, ray.direction, index, uv, N, st);
// Vector3f tmp = hitPoint;
switch (m->getType()) {
case REFLECTION_AND_REFRACTION:
{
Vector3f reflectionDirection = normalize(reflect(ray.direction, N));
Vector3f refractionDirection = normalize(refract(ray.direction, N, m->ior));
Vector3f reflectionRayOrig = (dotProduct(reflectionDirection, N) < 0) ?
hitPoint - N * EPSILON :
hitPoint + N * EPSILON;
Vector3f refractionRayOrig = (dotProduct(refractionDirection, N) < 0) ?
hitPoint - N * EPSILON :
hitPoint + N * EPSILON;
Vector3f reflectionColor = castRay(Ray(reflectionRayOrig, reflectionDirection), depth + 1);
Vector3f refractionColor = castRay(Ray(refractionRayOrig, refractionDirection), depth + 1);
float kr;
fresnel(ray.direction, N, m->ior, kr);
hitColor = reflectionColor * kr + refractionColor * (1 - kr);
break;
}
case REFLECTION:
{
float kr;
fresnel(ray.direction, N, m->ior, kr);
Vector3f reflectionDirection = reflect(ray.direction, N);
Vector3f reflectionRayOrig = (dotProduct(reflectionDirection, N) < 0) ?
hitPoint + N * EPSILON :
hitPoint - N * EPSILON;
hitColor = castRay(Ray(reflectionRayOrig, reflectionDirection),depth + 1) * kr;
break;
}
default:
{
// [comment]
// We use the Phong illumation model int the default case. The phong model
// is composed of a diffuse and a specular reflection component.
// [/comment]
Vector3f lightAmt = 0, specularColor = 0;
Vector3f shadowPointOrig = (dotProduct(ray.direction, N) < 0) ?
hitPoint + N * EPSILON :
hitPoint - N * EPSILON;
// [comment]
// Loop over all lights in the scene and sum their contribution up
// We also apply the lambert cosine law
// [/comment]
for (uint32_t i = 0; i < get_lights().size(); ++i)
{
auto area_ptr = dynamic_cast<AreaLight*>(this->get_lights()[i].get());
if (area_ptr)
{
// Do nothing for this assignment
}
else
{
Vector3f lightDir = get_lights()[i]->position - hitPoint;
// square of the distance between hitPoint and the light
float lightDistance2 = dotProduct(lightDir, lightDir);
lightDir = normalize(lightDir);
float LdotN = std::max(0.f, dotProduct(lightDir, N));
Object *shadowHitObject = nullptr;
float tNearShadow = kInfinity;
// is the point in shadow, and is the nearest occluding object closer to the object than the light itself?
bool inShadow = bvh->Intersect(Ray(shadowPointOrig, lightDir)).happened;
lightAmt += (1 - inShadow) * get_lights()[i]->intensity * LdotN;
Vector3f reflectionDirection = reflect(-lightDir, N);
specularColor += powf(std::max(0.f, -dotProduct(reflectionDirection, ray.direction)),
m->specularExponent) * get_lights()[i]->intensity;
}
}
hitColor = lightAmt * (hitObject->evalDiffuseColor(st) * m->Kd + specularColor * m->Ks);
break;
}
}
}
return hitColor;
}
这个时候再进一步看intersect函数,这里实际上就是去使用构造好的bvh求交点了。(怎么构造BVH,后面会详细阐述,先继续看下去)
Intersection Scene::intersect(const Ray &ray) const
{
return this->bvh->Intersect(ray);
}
继续往下看,此时会调用下面的函数,其中getIntersection函数里的内容就是作业之一(这部分后面会详细阐述),简单来说就是利用BVH求出交点。
Intersection BVHAccel::Intersect(const Ray& ray) const
{
Intersection isect;
if (!root)
return isect;
isect = BVHAccel::getIntersection(root, ray);
return isect;
}
Intersection BVHAccel::getIntersection(BVHBuildNode* node, const Ray& ray) const
{
// TODO Traverse the BVH to find intersection
std::array<int, 3> dirIsNeg = { (ray.direction.x > 0), (ray.direction.y > 0), (ray.direction.z > 0) };
Intersection isect;
isect.happened = node->bounds.IntersectP(ray, ray.direction_inv, dirIsNeg);
if (!isect.happened) return isect;
if (node->left == nullptr && node->right == nullptr)
return node->object->getIntersection(ray);
Intersection isect1,isect2;
isect1 = getIntersection(node->left, ray);
isect2 = getIntersection(node->right, ray);
if (isect1.distance < isect2.distance)
return isect1;
else
return isect2;
}
然后还有上面遗留的问题,就是BVH是如何构造的,主要就是这一段代码,构造方法也很简单,就是老师ppt里面提到的那个NAIVE规则,按最长轴切分,取中间的三角形为划分界限,划出两个子包围盒作为左右节点。
然后有个小细节,就是BVH是在代码中什么时候被构造的,其实这里有两个地方进行了BVH的构造,分别是在MeshTriangle(const std::string& filename)和void Scene::buildBVH()中,简单来说就是对模型整体构造了一个BVH,然后对整个场景又构造了一次BVH(该BVH只包含了一个模型,因此是叶子节点)。在渲染求交点的时候,会先利用场景的BVH进行判断,此时场景的BVH是叶子节点,如果和模型的包围盒有交点,就会通过node->object->getIntersection(ray)去调用模型的BVH继续求交点,之所以这么设计,是因为模型由三角形组成,可以说是内部又嵌套了一层。
BVHAccel::BVHAccel(std::vector<Object*> p, int maxPrimsInNode,
SplitMethod splitMethod)
: maxPrimsInNode(std::min(255, maxPrimsInNode)), splitMethod(splitMethod),
primitives(std::move(p))
{
time_t start, stop;
time(&start);
if (primitives.empty())
return;
if (splitMethod == SplitMethod::NAIVE)
{
root = recursiveBuild(primitives);
printf("Using NAIVE SplitMethod\n");
}
else if (splitMethod == SplitMethod::SAH)
{
root = recursiveBuildBySAH(primitives);
printf("Using SAH SplitMethod\n");
}
time(&stop);
double diff = difftime(stop, start);
int hrs = (int)diff / 3600;
int mins = ((int)diff / 60) - (hrs * 60);
int secs = (int)diff - (hrs * 3600) - (mins * 60);
printf(
"\rBVH Generation complete: \nTime Taken: %i hrs, %i mins, %i secs\n\n",
hrs, mins, secs);
}
BVHBuildNode* BVHAccel::recursiveBuild(std::vector<Object*> objects)
{
BVHBuildNode* node = new BVHBuildNode();
// Compute bounds of all primitives in BVH node
Bounds3 bounds;
for (int i = 0; i < objects.size(); ++i)
bounds = Union(bounds, objects[i]->getBounds());
if (objects.size() == 1) {
// Create leaf _BVHBuildNode_
node->bounds = objects[0]->getBounds();
node->object = objects[0];
node->left = nullptr;
node->right = nullptr;
return node;
}
else if (objects.size() == 2) {
node->left = recursiveBuild(std::vector{objects[0]});
node->right = recursiveBuild(std::vector{objects[1]});
node->bounds = Union(node->left->bounds, node->right->bounds);
return node;
}
else {
Bounds3 centroidBounds;
for (int i = 0; i < objects.size(); ++i)
centroidBounds =
Union(centroidBounds, objects[i]->getBounds().Centroid());
int dim = centroidBounds.maxExtent();
switch (dim) {
case 0:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().x <
f2->getBounds().Centroid().x;
});
break;
case 1:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().y <
f2->getBounds().Centroid().y;
});
break;
case 2:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().z <
f2->getBounds().Centroid().z;
});
break;
}
auto beginning = objects.begin();
auto middling = objects.begin() + (objects.size() / 2);
auto ending = objects.end();
auto leftshapes = std::vector<Object*>(beginning, middling);
auto rightshapes = std::vector<Object*>(middling, ending);
assert(objects.size() == (leftshapes.size() + rightshapes.size()));
node->left = recursiveBuild(leftshapes);
node->right = recursiveBuild(rightshapes);
node->bounds = Union(node->left->bounds, node->right->bounds);
}
return node;
}
作业一:光线生成
就是把作业5的改改。
void Renderer::Render(const Scene& scene)
{
std::vector<Vector3f> framebuffer(scene.width * scene.height);
float scale = tan(deg2rad(scene.fov * 0.5));
float imageAspectRatio = scene.width / (float)scene.height;
Vector3f eye_pos(-1, 5, 10);
int m = 0;
for (uint32_t j = 0; j < scene.height; ++j) {
for (uint32_t i = 0; i < scene.width; ++i) {
// generate primary ray direction
float x = (2 * (i + 0.5) / (float)scene.width - 1) *
imageAspectRatio * scale;
float y = (1 - 2 * (j + 0.5) / (float)scene.height) * scale;
// TODO: Find the x and y positions of the current pixel to get the
// direction
// vector that passes through it.
// Also, don't forget to multiply both of them with the variable
// *scale*, and x (horizontal) variable with the *imageAspectRatio*
// Don't forget to normalize this direction!
Vector3f dir = Vector3f(x, y, -1); // Don't forget to normalize this direction!
dir = normalize(dir);
Ray ray = Ray(eye_pos, dir);
framebuffer[m++] = scene.castRay(ray, 0);
}
UpdateProgress(j / (float)scene.height);
}
UpdateProgress(1.f);
// save framebuffer to file
FILE* fp = fopen("binary.ppm", "wb");
(void)fprintf(fp, "P6\n%d %d\n255\n", scene.width, scene.height);
for (auto i = 0; i < scene.height * scene.width; ++i) {
static unsigned char color[3];
color[0] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].x));
color[1] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].y));
color[2] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].z));
fwrite(color, 1, 3, fp);
}
fclose(fp);
}
作业二:光线-三角形相交
一样,就是把作业5的改改。
inline Intersection Triangle::getIntersection(Ray ray)
{
Intersection inter;
if (dotProduct(ray.direction, normal) > 0)
return inter;
double u, v, t_tmp = 0;
Vector3f pvec = crossProduct(ray.direction, e2);
double det = dotProduct(e1, pvec);
if (fabs(det) < EPSILON)
return inter;
double det_inv = 1. / det;
Vector3f tvec = ray.origin - v0;
u = dotProduct(tvec, pvec) * det_inv;
if (u < 0 || u > 1)
return inter;
Vector3f qvec = crossProduct(tvec, e1);
v = dotProduct(ray.direction, qvec) * det_inv;
if (v < 0 || u + v > 1)
return inter;
t_tmp = dotProduct(e2, qvec) * det_inv;
// TODO find ray triangle intersection
if (t_tmp < 0)
return inter;
//去看Sphere那个函数的写法就行
inter.happened = true;
inter.coords = ray(t_tmp);
inter.normal = normal;
inter.distance = t_tmp;
inter.obj = this;
inter.m = this->m;
return inter;
}
作业三:包围盒与光线相交
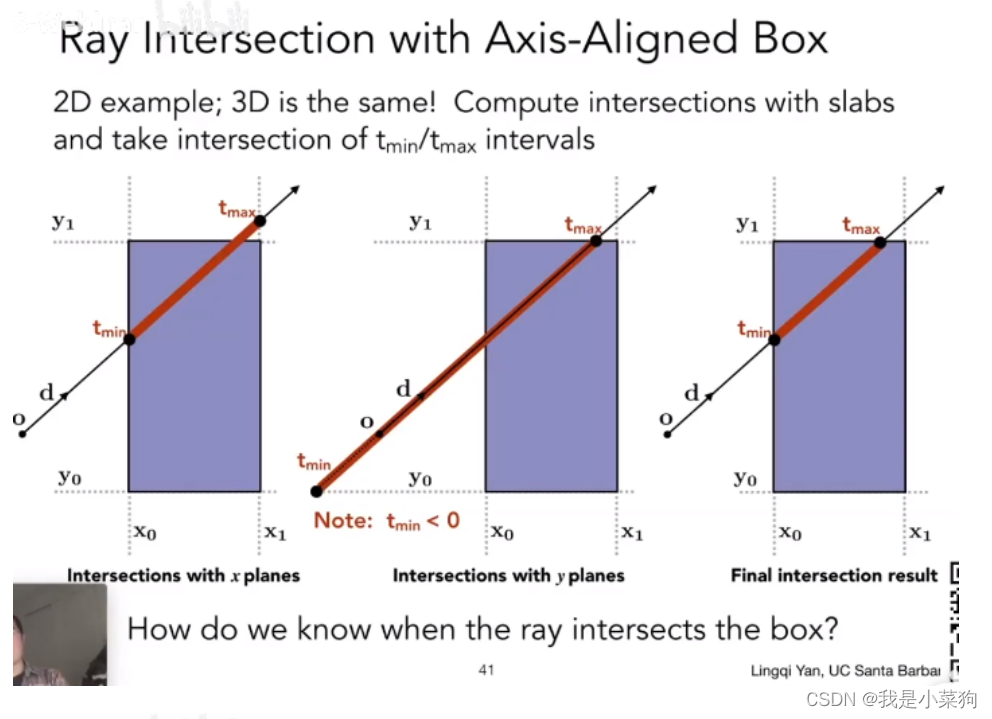
不难,老师的ppt已经讲得很清楚了。核心本质就是当光线进入盒子中时,必然点进入了所有的对面(对应max(tmin)),当光线离开盒子时,必然离开了某一个对面(对应min(tmax)),所以才会有max和min的处理。


inline bool Bounds3::IntersectP(const Ray& ray, const Vector3f& invDir,
const std::array<int, 3>& dirIsNeg) const
{
// invDir: ray direction(x,y,z), invDir=(1.0/x,1.0/y,1.0/z), use this because Multiply is faster that Division
// dirIsNeg: ray direction(x,y,z), dirIsNeg=[int(x>0),int(y>0),int(z>0)], use this to simplify your logic
// TODO test if ray bound intersects
//注:dirIsNeg我觉得没必要用,我感觉我这种逻辑更容易理解,更小的t肯定是min
float t1,t2,t_min_x, t_max_x, t_min_y, t_max_y, t_min_z, t_max_z, t_enter, t_exit;
t1 = (pMin.x - ray.origin.x) * invDir.x; t2 = (pMax.x - ray.origin.x) * invDir.x;
t_min_x = fminf(t1, t2); t_max_x = fmaxf(t1, t2);
t1 = (pMin.y - ray.origin.y) * invDir.y; t2 = (pMax.y - ray.origin.y) * invDir.y;
t_min_y = fminf(t1, t2); t_max_y = fmaxf(t1, t2);
t1 = (pMin.z - ray.origin.z) * invDir.z; t2 = (pMax.z - ray.origin.z) * invDir.z;
t_min_z = fminf(t1, t2); t_max_z = fmaxf(t1, t2);
t_exit = fminf(fminf(t_max_x, t_max_y), t_max_z);
if (t_exit < 0) return false;
t_enter = fmaxf(fmaxf(t_min_x, t_min_y), t_min_z);
if (t_enter >= t_exit)return false;
return true;
}
作业四:使用BVH求交
也不难,主要是看懂框架,然后照着老师ppt的伪代码写就行。
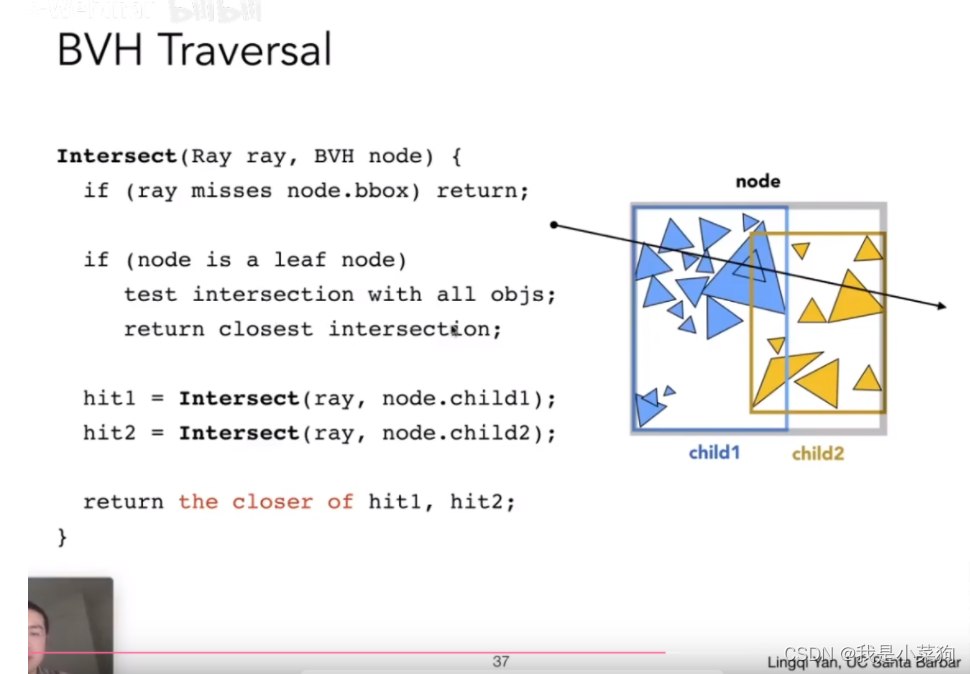
Intersection BVHAccel::getIntersection(BVHBuildNode* node, const Ray& ray) const
{
// TODO Traverse the BVH to find intersection
std::array<int, 3> dirIsNeg = { (ray.direction.x > 0), (ray.direction.y > 0), (ray.direction.z > 0) };
Intersection isect;
isect.happened = node->bounds.IntersectP(ray, ray.direction_inv, dirIsNeg);
if (!isect.happened) return isect;
if (node->left == nullptr && node->right == nullptr)
return node->object->getIntersection(ray);
Intersection isect1,isect2;
isect1 = getIntersection(node->left, ray);
isect2 = getIntersection(node->right, ray);
if (isect1.distance < isect2.distance)
return isect1;
else
return isect2;
}
扩展:使用SAH规则构建BVH,从而加速BVH求交
但其实上述代码使用的NAIVE划分方法在面对不均匀场景的时候效果一般(会有很多空间冗余,光线与这个包围盒相交,但是真正与物体相交的概率却不大),如下图。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kPyt759B-1672851153723)(C:\Users\lenovo\AppData\Roaming\Typora\typora-user-images\image-20230104202307647.png)]](https://img-blog.csdnimg.cn/2e30a129c1b6454589680da784550ea3.png)
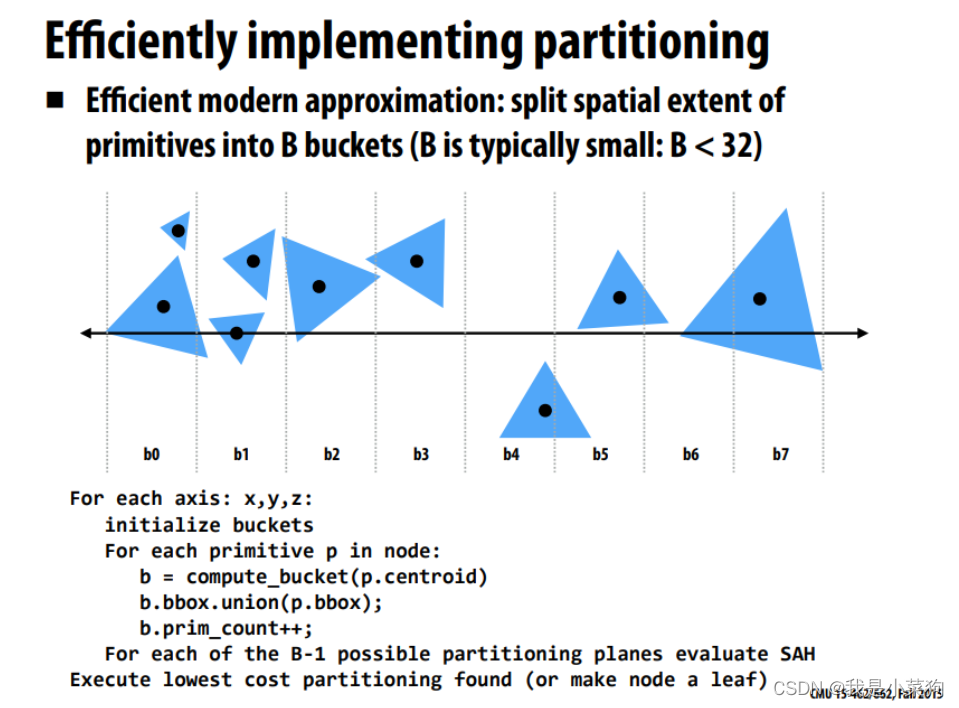
SAH划分方法实际上是NAIVE划分方法的进一步优化,SAH划分也很简单其实,就是在待定的划分中,通过计算相应划分的cost,取最小cost,从而得到最优划分。这就涉及到两个环节,第一:怎么得到待定的划分?它这里的方法就是依次遍历三个轴,然后每个轴根据物体的数量划分成特定数量的桶,利用桶就能得到一个又一个的划分。第二:怎么计算cost,也就是如何评价这次划分好还是不好?cost的计算方法已经由下图给出,还是比较简单的,就是要抽象出划分之后,直线与这个大包围盒相交的代价(可以简单理解为计算开销),下图公式将其抽象成了三个部分,第一是一些基本的固定开销(直线和大包围盒的相交判断,直线和两个子包围盒的相交判断),然后第二和第三加起来就是划分出来的两个子包围盒带来的期望开销(就是说如果直线与子包围盒有相交,那就要计算直线与子包围盒里面全部物体相交所带来的开销,但是直线是不一定与子包围盒相交的,所以前面要乘上直线与子包围盒相交的概率),其中直线与子包围盒相交的概率由大包围盒与子包围盒的表面积之比求出(有点奇怪为啥不用体积,体积不是更合适点嘛==),直线与子包围盒内全部物体相交带来的开销可以自定义(代码里面就简化为了包围盒里物体的数量×1,当然这边可以更复杂,比如不同的物体会带来不同的开销)。



BVHBuildNode* BVHAccel::recursiveBuildBySAH(std::vector<Object*> objects)
{
int Bucket_num = 10;
if(objects.size()< Bucket_num)
return recursiveBuild(objects);
BVHBuildNode* node = new BVHBuildNode();
double minCost = std::numeric_limits<double>::infinity();
int mindim, split_index;
for (int dim = 0; dim < 3; dim++)
{
//按x,y,z轴排序
switch (dim) {
case 0:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().x <
f2->getBounds().Centroid().x;
});
break;
case 1:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().y <
f2->getBounds().Centroid().y;
});
break;
case 2:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().z <
f2->getBounds().Centroid().z;
});
break;
}
Bounds3 bounds;
for (int i = 0; i < objects.size(); ++i)
bounds = Union(bounds, objects[i]->getBounds());
Bounds3 bucketA;
int p_in_bucket_num , p_in_bucketA_num, p_in_bucketB_num;
p_in_bucket_num = objects.size() / Bucket_num;
p_in_bucketA_num = 0;
p_in_bucketB_num = 0;
for (int Bucket_index = 0; Bucket_index < Bucket_num-1; Bucket_index++)
{
int i;
for (i = 0; i < p_in_bucket_num; i++)
{
bucketA = Union(bucketA, objects[Bucket_index* p_in_bucket_num+i]->getBounds());
p_in_bucketA_num++;
}
Bounds3 bucketB;
for (int j = Bucket_index * p_in_bucket_num + i; j < objects.size(); j++)
{
bucketB = Union(bucketB, objects[j]->getBounds());
}
p_in_bucketB_num = objects.size() - p_in_bucketA_num;
double cost = (bucketA.SurfaceArea() * p_in_bucketA_num + bucketB.SurfaceArea() * p_in_bucketB_num) / bounds.SurfaceArea();
if (minCost > cost)
{
minCost = cost;
mindim = dim;
split_index = p_in_bucketA_num;
}
}
}
switch (mindim) {
case 0:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().x <
f2->getBounds().Centroid().x;
});
break;
case 1:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().y <
f2->getBounds().Centroid().y;
});
break;
case 2:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().z <
f2->getBounds().Centroid().z;
});
break;
}
auto beginning = objects.begin();
auto middling = objects.begin() + (split_index);
auto ending = objects.end();
auto leftshapes = std::vector<Object*>(beginning, middling);
auto rightshapes = std::vector<Object*>(middling, ending);
assert(objects.size() == (leftshapes.size() + rightshapes.size()));
node->left = recursiveBuild(leftshapes);
node->right = recursiveBuild(rightshapes);
node->bounds = Union(node->left->bounds, node->right->bounds);
return node;
}
看得更深一点,就是实际上这个cost的作用(从公式本身去看他),就是让子包围盒的表面积尽可能小(减少冗余空间,说明光线若与这个包围盒相交,那么我们会希望交点大概率是在这个包围盒内部),同时,在物体必须全部被两个子包围盒囊括的情况下,小的子包围盒倾向于装更多且相交开销大的物体(光线与小的包围盒求交,相交概率不大,由此就能尽可能避免与内部物体相交产生的额外开销),另一个大点的子包围盒倾向于装更少且相交开销小的物体(光线与大的包围盒求交,相交概率大,由此可以最小化与内部物体相交产生的开销)。一个原则,把光线与物体的相交计算用在真正正确的地方。
至于为什么这样的cost会解决不均匀的问题,好吧,我尝试思考了一个晚上,回答不了,想的头痛,就这样吧。因为我在思考的时候遇到了一个矛盾的点,一直想不通,擦,就是均匀意味着大的子包围盒要有更多的物体(不会有空间冗余,但是计算开销大),而这个cost方法会倾向于让大的子包围盒有更少的物体(会有空间冗余,但是计算开销小)。那你说,tmd,哪个更好呢?我擦,虽然这是简单逻辑,但其实并不好想通,也许,这就是两个矛盾的,想通不了==
等下,这有点感觉像博弈,就是说第一种情况的话,我倾向于高风险高收益(认为大包围盒大概率能找到交点,就想在大包围盒里面找到交点,所以加很多物体进去),第二种情况的话我倾向于低风险低收益(认为大包围盒大概率找不到交点,想早点跳过大包围盒,所以加尽可能少的物体进去)。
算了,不想了,头晕。
tmd,就先这么理解,就是说,让子包围盒的表面积尽可能小这一步就已经让其实现了均匀划分的效果(包围盒被尽可能的压缩了),然后之后的大的子包围盒有更少的物体这个倾向就是SAH在保持均匀划分效果下的进一步优化。
最终效果
至于渲染速度的话,读者有时间可以用自己电脑对比一下优化前和优化后,我的电脑太老了,渲染时间都得接近30,我这边优化前和优化后的速度差别不大,偶尔差个一两秒,看其他博主结果好像快的也不多,可能是场景还不够复杂没有充分体现出来==

感悟
tmd,写到半夜1点,本来是不想写的,但是想了想可能会对其他后来人有用,还是坚持写完了,害,可能我的理解会有一些错误,如有错误,还望读者见谅==
参考链接
1.https://zhuanlan.zhihu.com/p/477316706
2.http://15462.courses.cs.cmu.edu/fall2015content/lectures/10_acceleration/10_acceleration_slides.pdf
3.https://blog.csdn.net/onion23/article/details/126625653(感觉这个老哥代码写的不错)
4.https://blog.csdn.net/qq_41835314/article/details/125073507
5.https://zhuanlan.zhihu.com/p/50720158
6.https://blog.csdn.net/weixin_44491423/article/details/127485933
7.https://blog.csdn.net/ycrsw/article/details/124331686