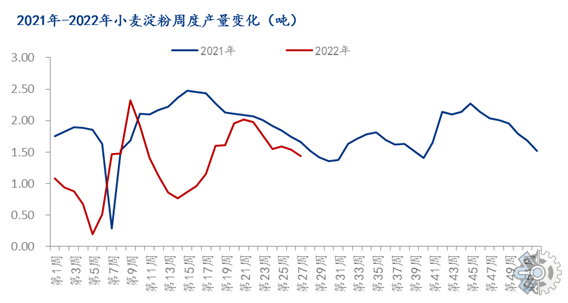
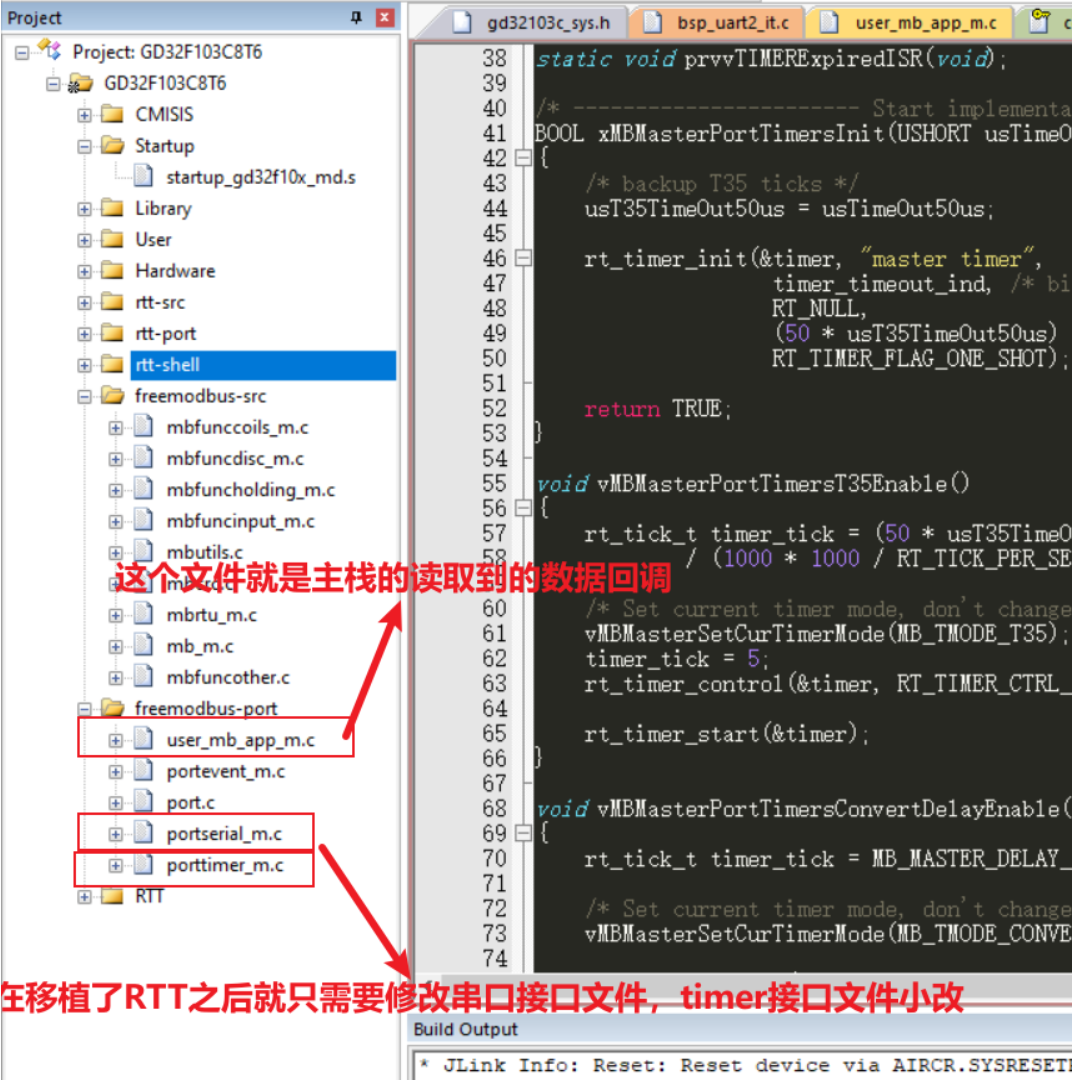
Resnet结构的有效性解释
先看一看Resnet网络的块结构:

根据上图,设有函数
z
(
l
)
=
x
(
l
−
1
)
+
F
(
x
)
(
l
−
1
)
(1)
\mathbf{z}^{(l)}=\mathbf{x}^{(l-1)}+\mathcal{F}(\mathbf{x})^{(l-1)}\tag{1}
z(l)=x(l−1)+F(x)(l−1)(1)
考虑由式
(
1
)
(1)
(1)组成的前馈神经网络,假设残差块不使用激活函数,那么整个式子仍然是线性变换,可得:
x
(
l
)
=
z
(
l
)
(2)
\mathbf{x}^{(l)}=\mathbf{z}^{(l)}\tag{2}
x(l)=z(l)(2)
考虑任意两个层数
l
2
>
l
1
l_2>l_1
l2>l1,联合
(
1
)
(1)
(1)式和
(
2
)
(2)
(2)式,将
x
\mathbf{x}
x进行递归展开
x
(
l
2
)
=
x
(
l
2
−
1
)
+
F
(
(
x
(
l
2
−
1
)
)
=
(
x
(
l
2
−
2
)
+
F
(
(
x
(
l
2
−
2
)
)
)
+
F
(
(
x
(
l
2
−
1
)
)
=
x
l
1
+
∑
l
=
l
1
l
2
−
1
F
(
x
(
l
)
)
\begin{align*} \mathbf{x}^{(l_2)}&=\mathbf{x}^{(l_2-1)}+\mathcal{F}\left((\mathbf{x}^{(l_2-1)}\right)\\ &=\left(\mathbf{x}^{(l_2-2)}+\mathcal{F}\left((\mathbf{x}^{(l_2-2)}\right)\right)+\mathcal{F}\left((\mathbf{x}^{(l_2-1)}\right)\\ &=\mathbf{x}^{l_1}+\sum_{l=l_1}^{l_2-1}{\mathcal{F}(\mathbf{x}^{(l)})}\tag{3} \end{align*}
x(l2)=x(l2−1)+F((x(l2−1))=(x(l2−2)+F((x(l2−2)))+F((x(l2−1))=xl1+l=l1∑l2−1F(x(l))(3)
根据式
(
3
)
(3)
(3),前向传播时,输入信号可以从任意低层直接传播到高层。这种天然的恒等映射在一定程度上解决了网络退化问题。
利用链式求导法则,网络前向传播的损失
L
L
L对某低层输出的梯度可以展开为:
∂
L
∂
x
(
l
1
)
=
∂
L
∂
x
(
l
2
)
∂
x
(
l
2
)
∂
x
(
l
1
)
=
∂
L
∂
x
(
l
2
)
(
1
+
∂
∂
x
(
l
1
)
∑
l
=
l
1
l
2
−
1
F
(
x
(
l
)
)
)
=
∂
L
∂
x
(
l
2
)
+
∂
L
∂
x
(
l
2
)
∂
∂
x
(
l
1
)
∑
l
=
l
1
l
2
−
1
F
(
x
(
l
)
)
\begin{align*} \frac{\partial L}{\partial \mathbf{x}^{(l_1)}}&=\frac{\partial L}{\partial \mathbf{x}^{(l_2)}}\frac{\partial \mathbf{x}^{(l_2)}}{\partial \mathbf{x}^{(l_1)}}\\ &=\frac{\partial L}{\partial \mathbf{x}^{(l_2)}}\left(1+\frac{\partial}{\partial \mathbf{x}^{(l_1)}}\sum_{l=l_1}^{l_2-1}{\mathcal{F}(\mathbf{x}^{(l)})}\right)\\ &=\frac{\partial L}{\partial \mathbf{x}^{(l_2)}}+\frac{\partial L}{\partial \mathbf{x}^{(l_2)}}\frac{\partial}{\partial \mathbf{x}^{(l_1)}}\sum_{l=l_1}^{l_2-1}{\mathcal{F}(\mathbf{x}^{(l)})}\tag{4} \end{align*}
∂x(l1)∂L=∂x(l2)∂L∂x(l1)∂x(l2)=∂x(l2)∂L(1+∂x(l1)∂l=l1∑l2−1F(x(l)))=∂x(l2)∂L+∂x(l2)∂L∂x(l1)∂l=l1∑l2−1F(x(l))(4)
根据式 ( 4 ) (4) (4),损失对某低层输出的梯度,被分解成了两项,第一项表明在反向传播时,信号可以直接传播到低层,从而缓解了梯度消失问题,即使中间层权重矩阵很小,梯度也不容易消失。