【深蓝学院】移动机器人运动规划--第1章运动规划介绍与地图构建--笔记

文章目录

1. Course introduction
2. Course Outline
- 2.1 课程概览
- 2.2 课程算法概览
- - 2.2.1 基于搜索的前端
  - 2.2.2 基于采样的前端
  - 2.2.3 满足动力学约束的路径搜索
  - 2.2.4 后端轨迹优化
3. 地图表示
- 3.1 Occupancy grid map占用栅格地图
- 3.2 八叉树地图
- 3.3 Voxel hashing（体素哈希）
- 3.4 piint cloud点云
- 3.5 TSDF 截断符号距离函数
- 3.6 ESDF欧式符号距离函数
- 3.7 More
4. Occupancy grid map
- 4.1 理论推导
- 4.2 occupancy Grid Map小结
5. Euclidean Signed Distance Field(ESDF)
- 5.1 计算步骤
- 5.2 ESDF代码
- 5.3 线性插值及梯度计算
6. Refernece

1. Course introduction

在这里插入图片描述
会：

模块化设计(学院派)的规划pipeline
希望能在实际机器上实现

不会

端到端导航（据我所知，强化学习做导航比较多）
详细的公式证明（可后面查阅paper）

运动规划在整个机器人技术栈中属于较为上层的部分。
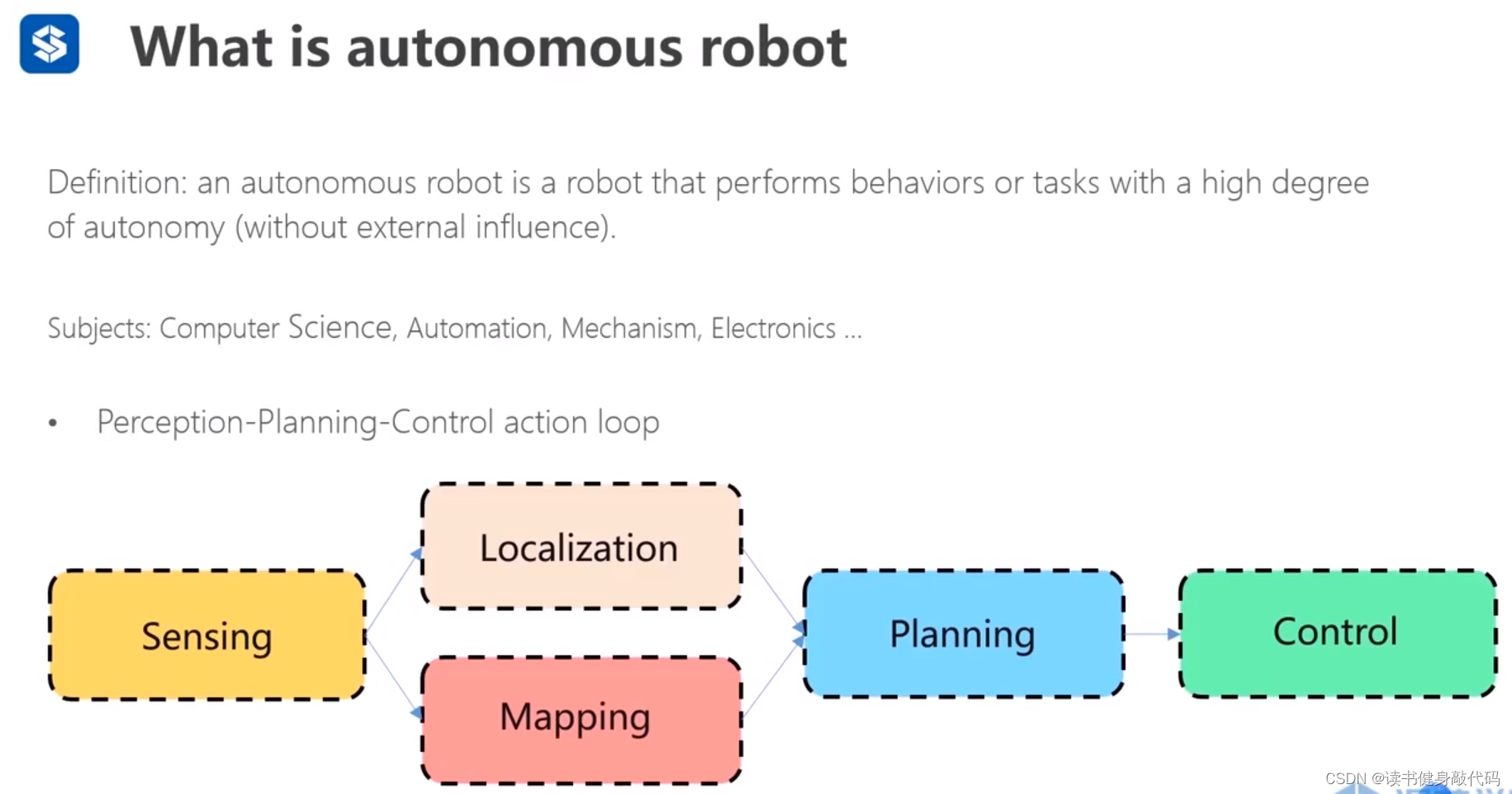
在这里插入图片描述
感知-规划-控制闭环（SLAM在感知层面）。

一些简单案例：
海陆空机器人均有
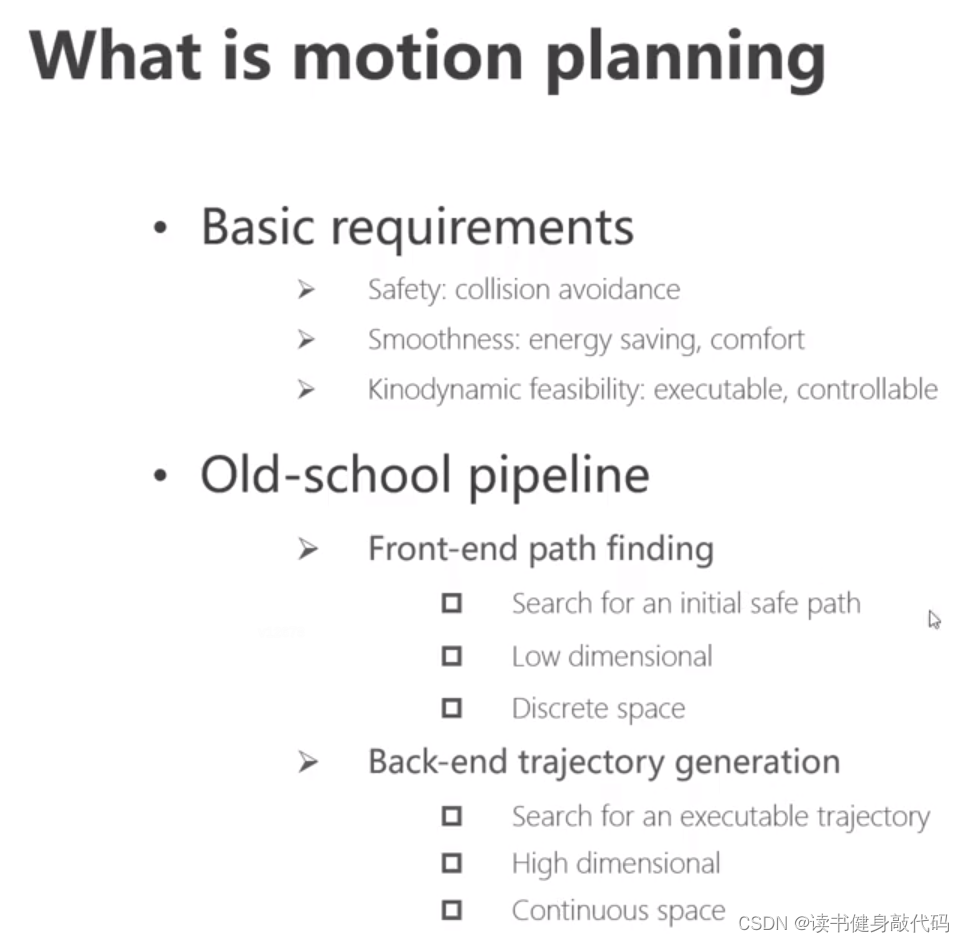
在这里插入图片描述

在这里插入图片描述

基础要求：

安全，不能碰撞
轨迹光滑：物理机上能源有限，轨迹要光滑，如果是拍摄则要考虑视频的流畅度，自动驾驶要考虑乘客的舒适度
动力学可行。

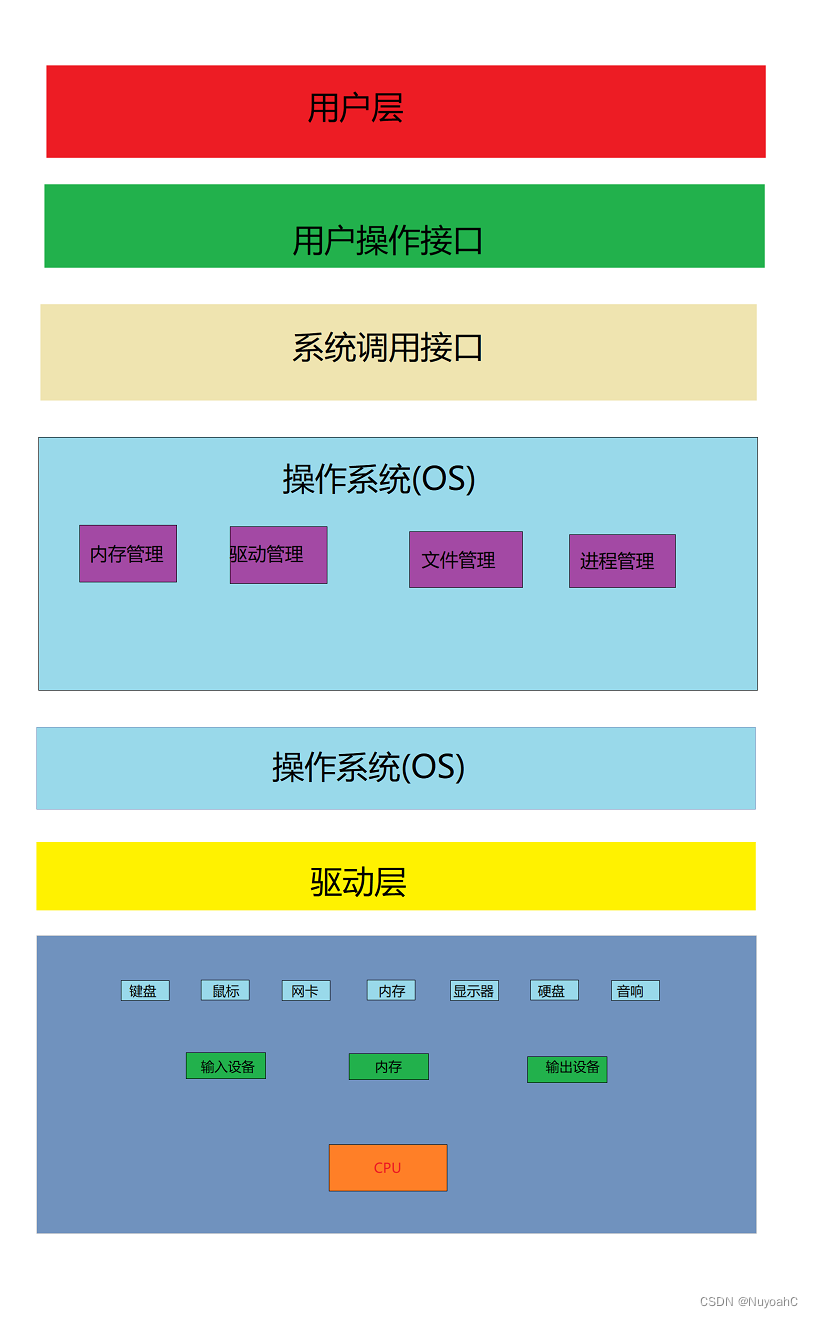
学院派pipeline：
planning同样也分为前后端：

前端主要生成粗略的、离散的路径，一般低维，不含具体的方向，速度大小等信息，称为path
后端根据path来进行优化，生成高维的、连续的、可执行的路径，称为trajectory

如何做机器人的研究：
在这里插入图片描述
在实际机器人上进行部署是学界亘古不变的道理？

在这里插入图片描述

要求规划领域的知识面需要广，对不同的场合设计不同的策略。
不要怕动手，robotics本身就很辛苦
出色的机器人工程师要对整个系统的各个部件都要熟知（感知，定位，控制），不要求开发，但是至少得维护。

2. Course Outline

2.1 课程概览

课程分为3部分：
前端path finding，后端trajectory generation，用于机器人规划的MPC

在这里插入图片描述

2.2 课程算法概览

基于搜索。DFS，BFS
基于采样。随机采样的思想，希望用越来越多的采样来覆盖环境中没有探索过的区域，去构成一个graph。

2.2.1 基于搜索的前端

在这里插入图片描述
与搜索算法对应的就是图，图中最重要的是结点和边（有向和无向边）：

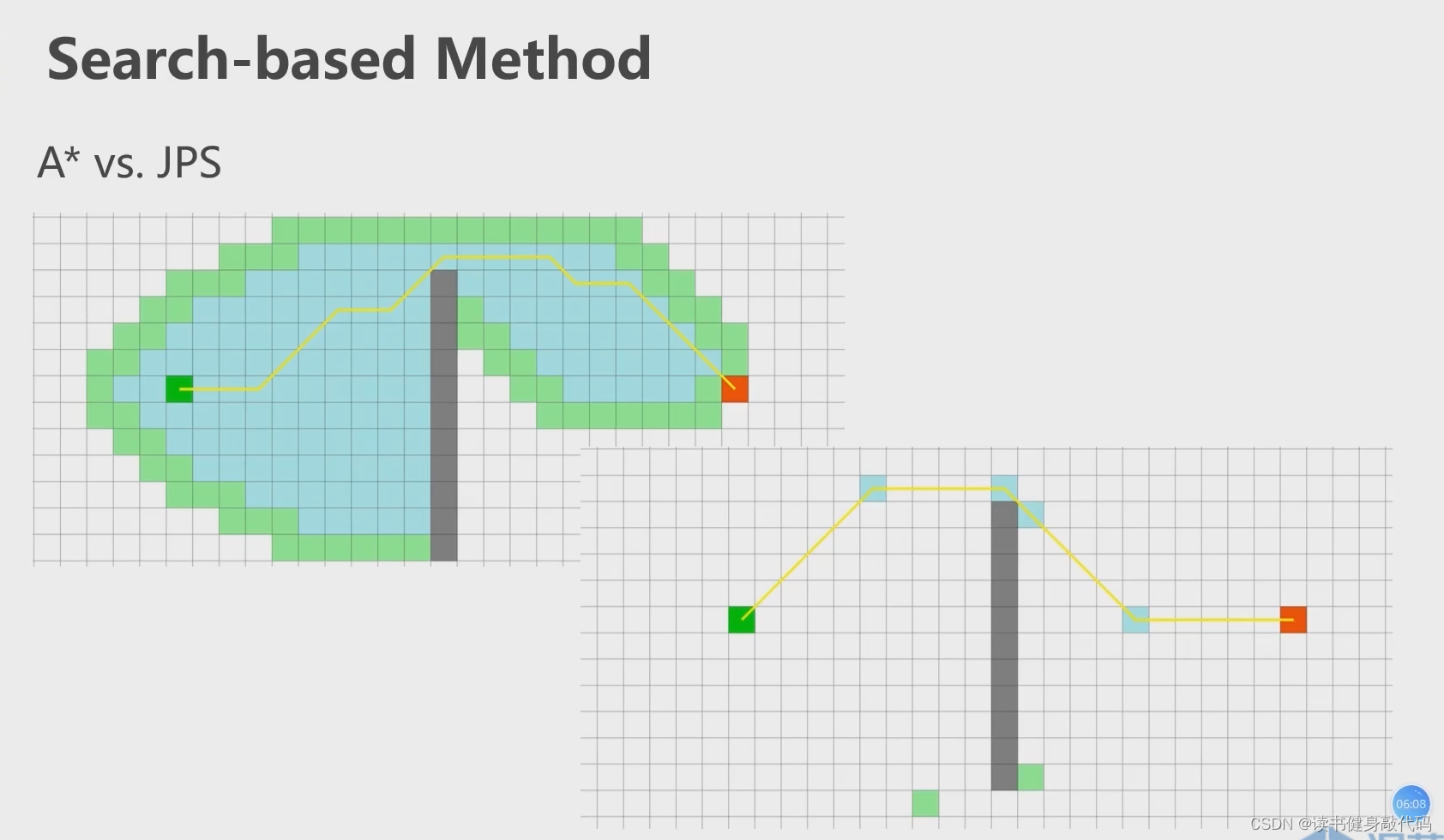
Dijkstra和A*目的不同，前者倾向于搜索全图，最短路径的cost较大，后者有指向性，很快找到最短路径。
在这里插入图片描述

JPS跳点搜索不一定比A*更好，需要看实际应用场景。
在这里插入图片描述

2.2.2 基于采样的前端

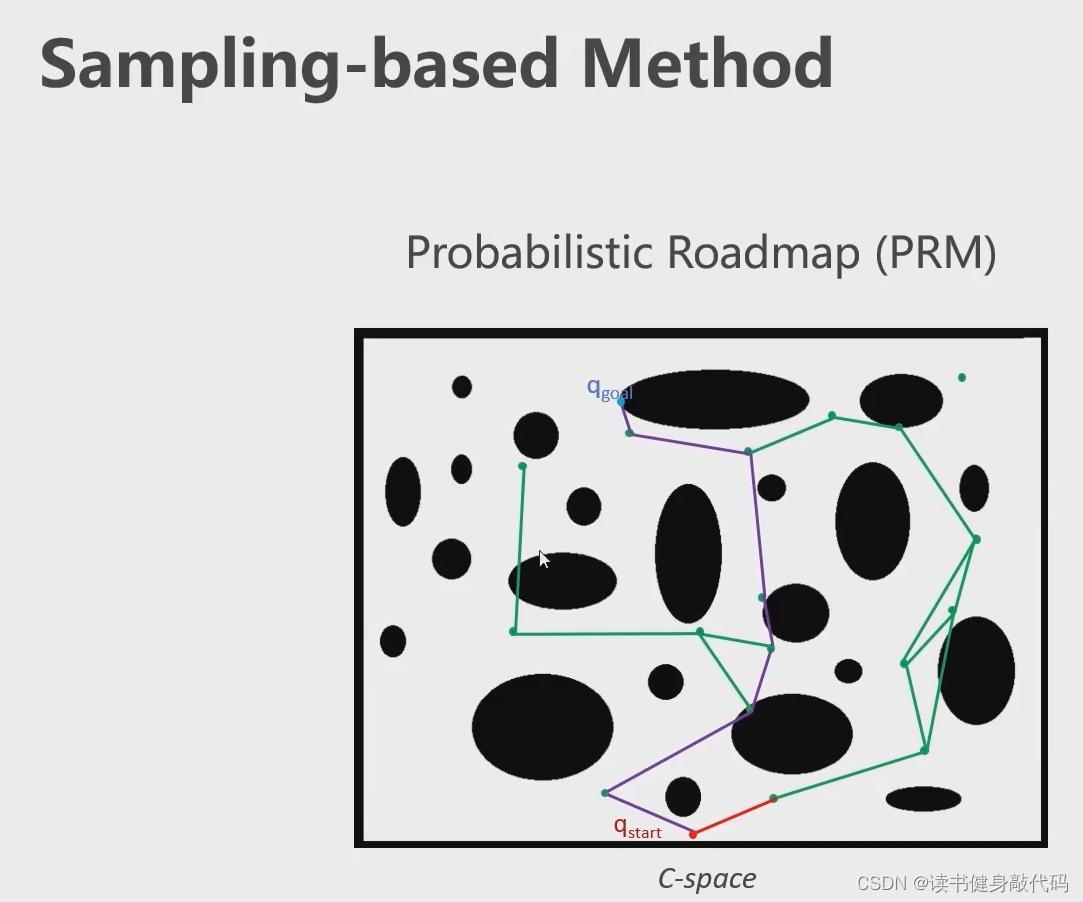
撒一些采样点，将不在障碍物内的边连起来，去掉在障碍物内的边，得到概率路线图(PRM)。
在这里插入图片描述

RRT本身不具备渐进最优性，RRT具备，下图左，两点间最优路径是接近直线，但RRT没找到直线，RRT维护的随机扩展树很顺滑，而RRT是杂乱无章。（Ch3主要讲）
在这里插入图片描述

informed RRT* 启发式RRT*，画一个椭圆（椭球），相当于给搜索范围框定了一个先验，在搜索范围内找
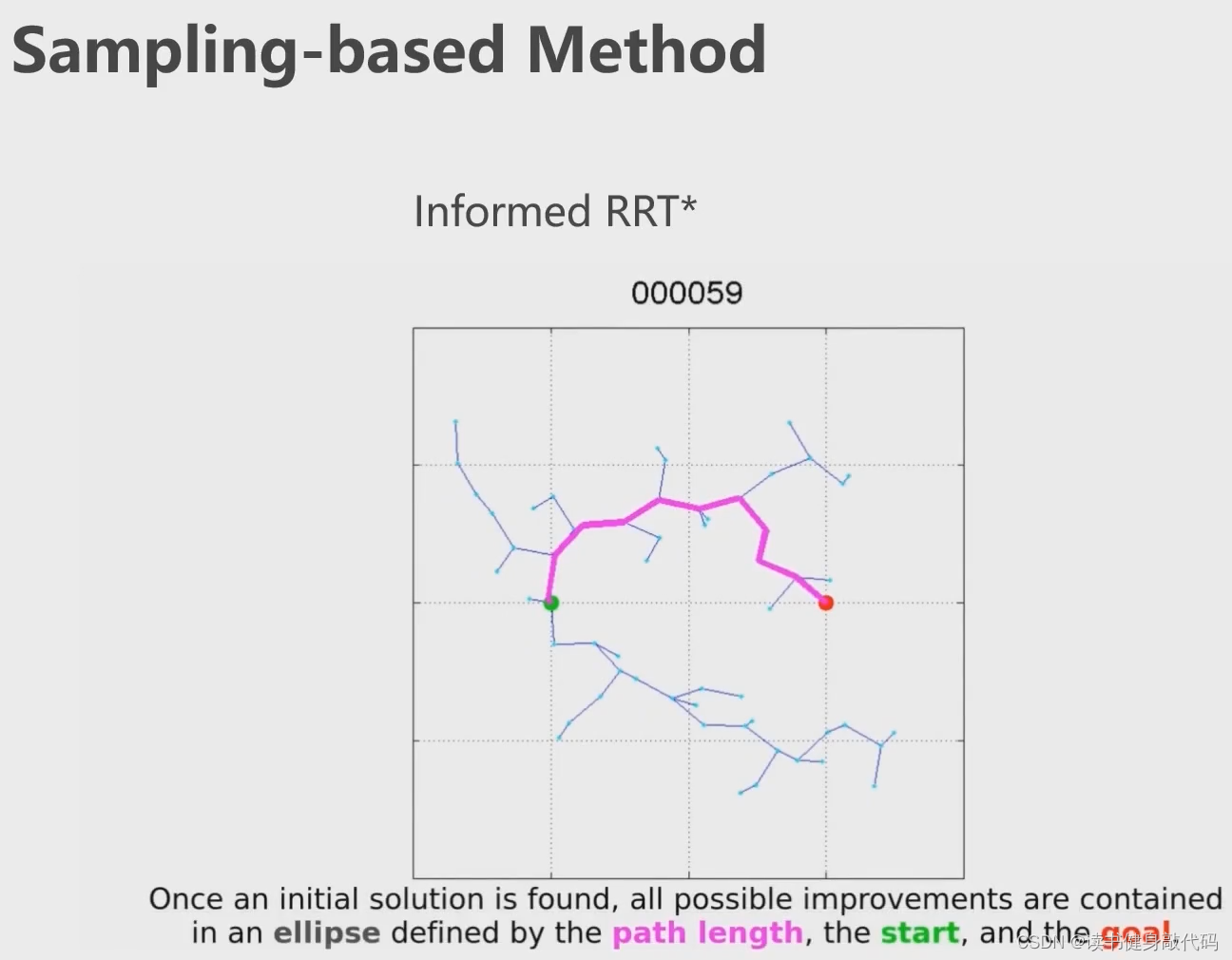
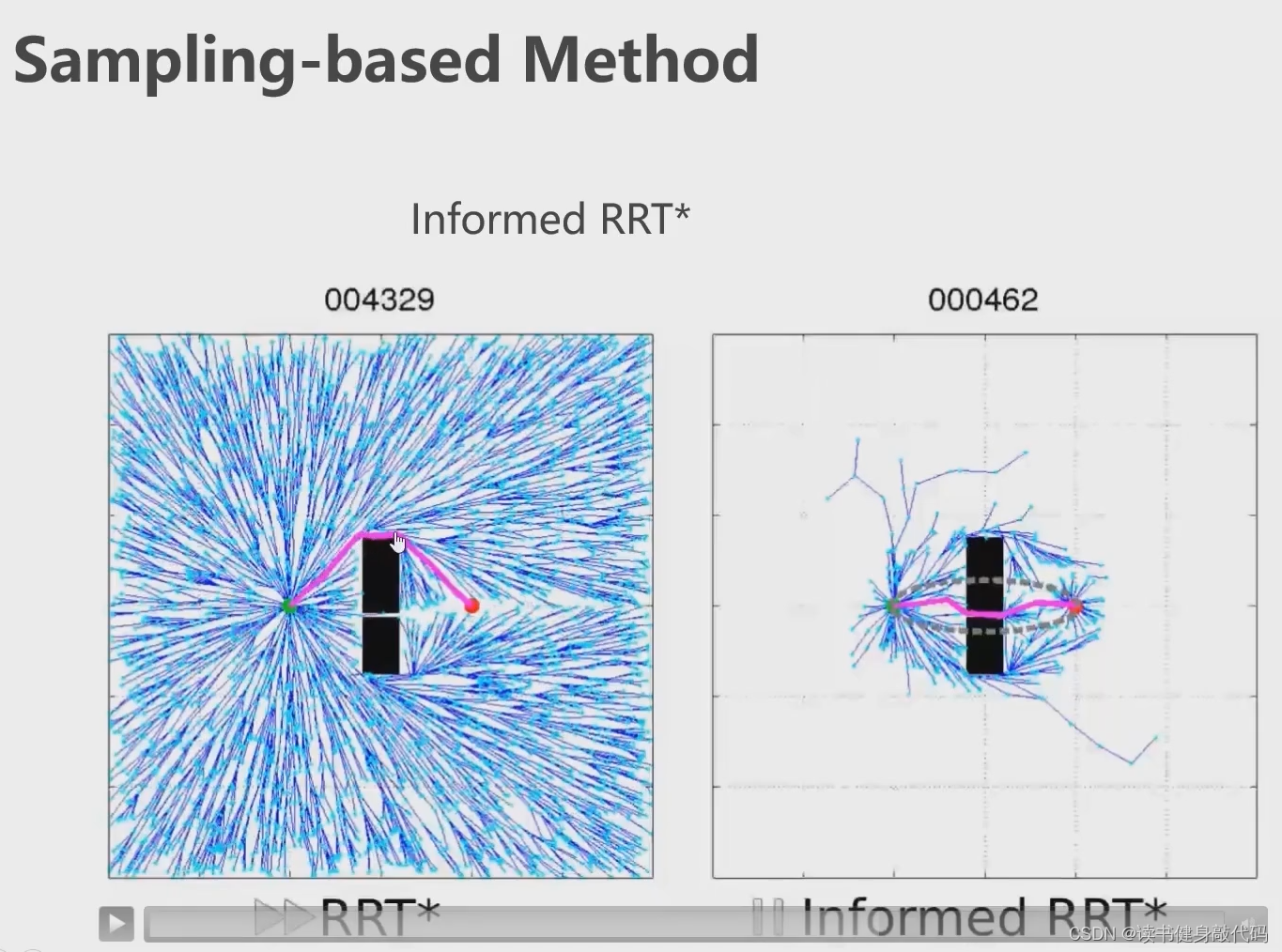
在这里插入图片描述

在这里插入图片描述

2.2.3 满足动力学约束的路径搜索

比如约束是起始和结束时的速度（大小，方向）。
1. hybrid A*
lattice search，机器人的控制方法，在某点给油或者打方向，遍历所有的可能组成一个控制组合，然后在本段控制终点继续这种组合模式。
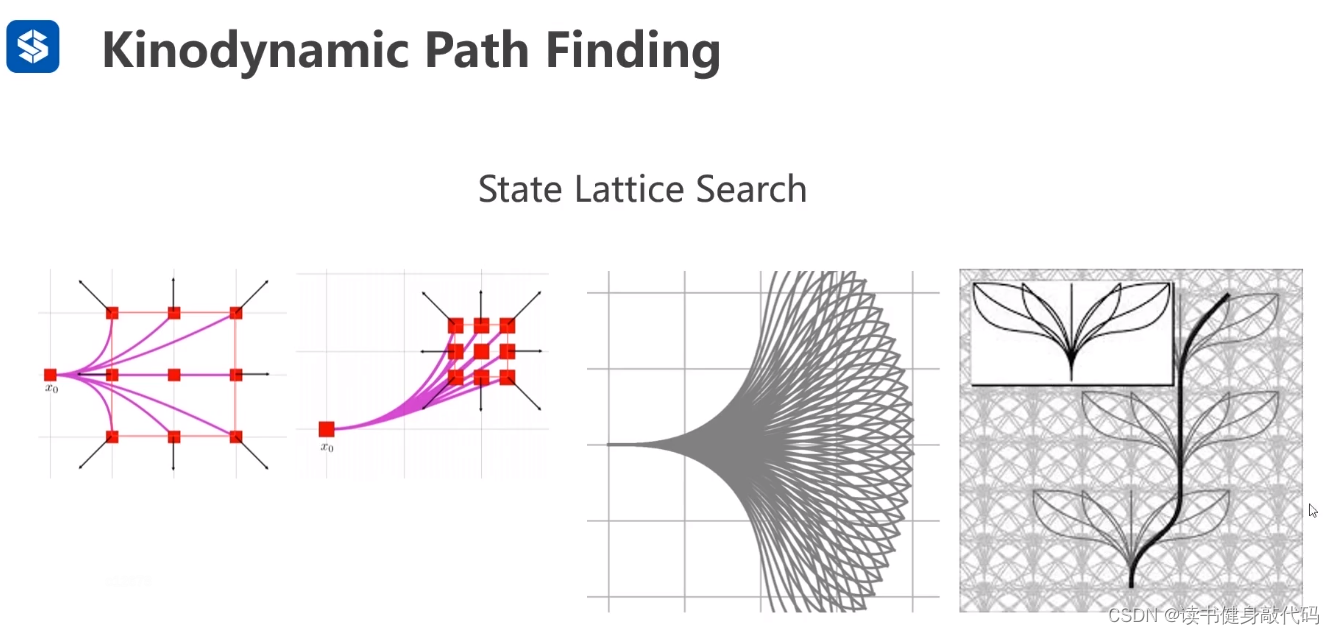
在这里插入图片描述
但是这样做cost很高，于是hybrid A*应运而生，维护一个栅格，每个栅格里面都有一个状态，找到更好的状态之后就会把之前的状态给删掉。

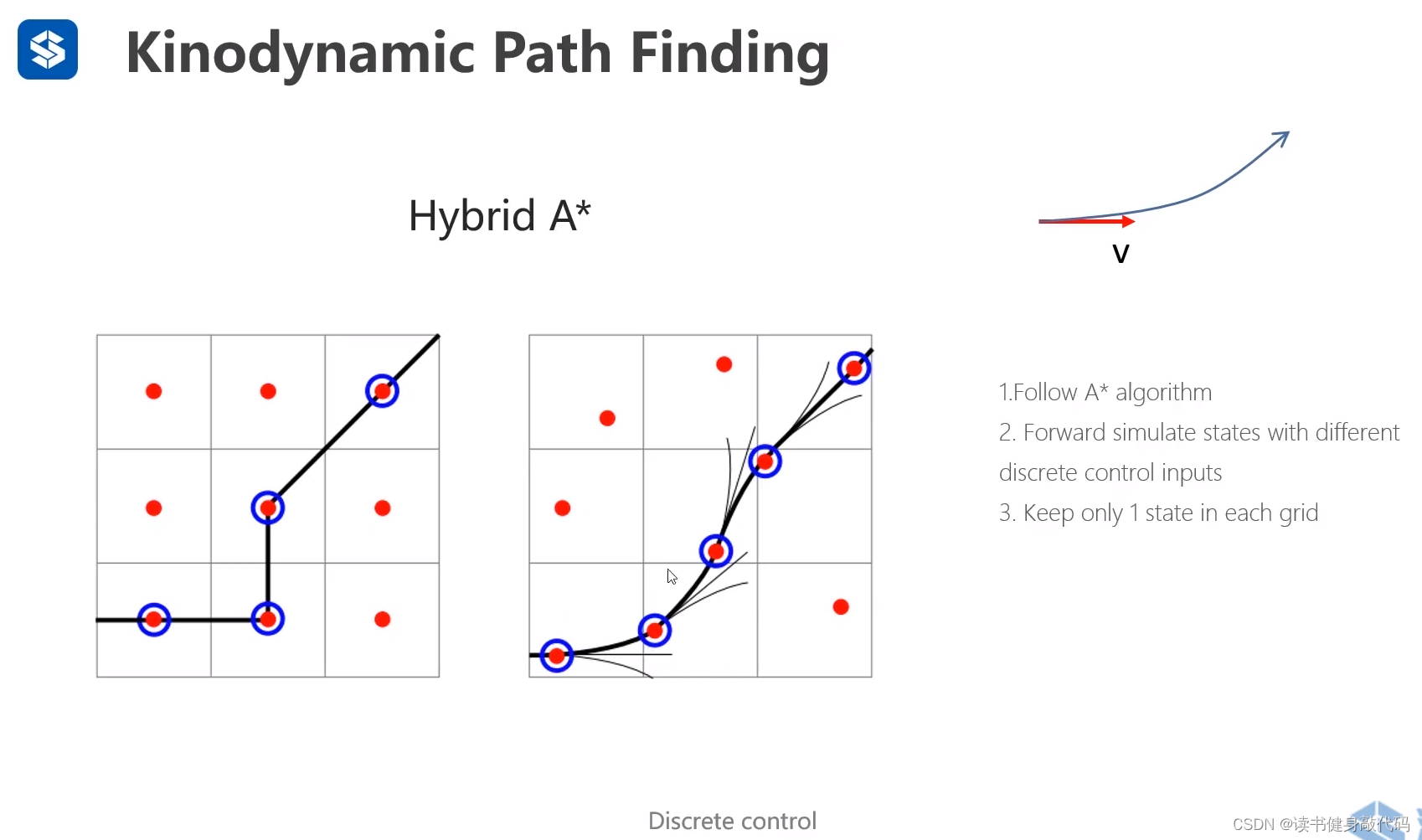
地面无人车导航，无人机导航。

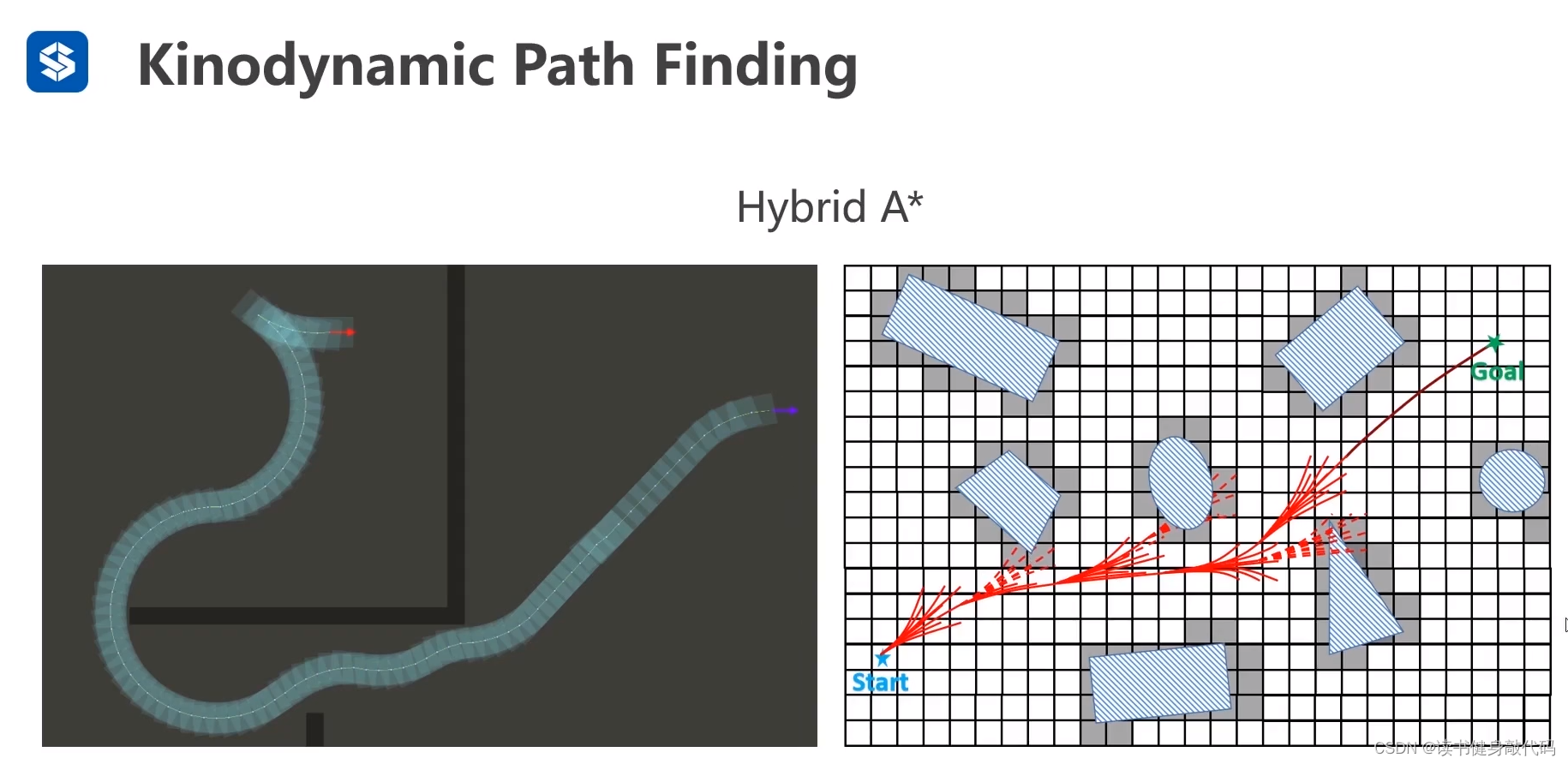
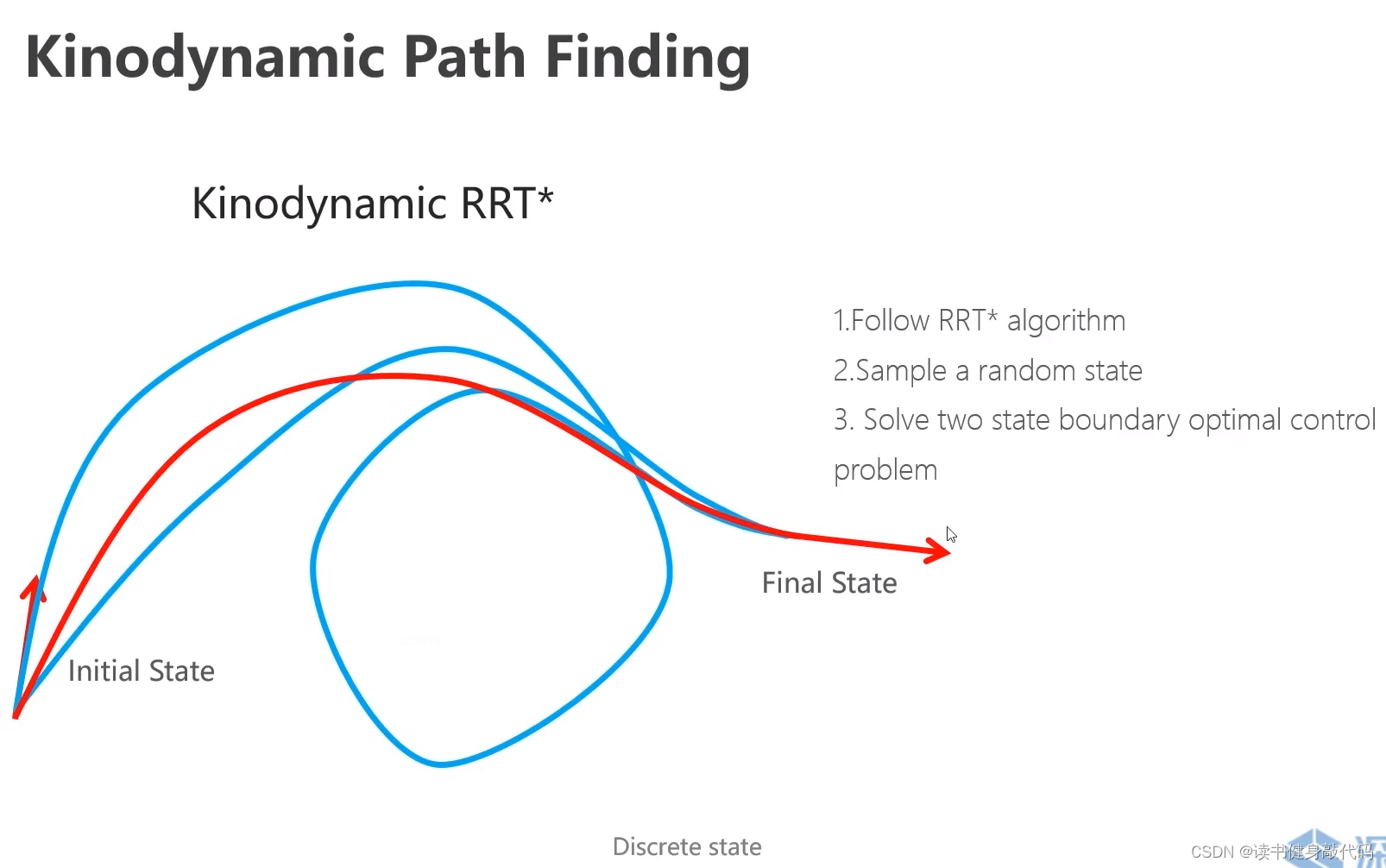
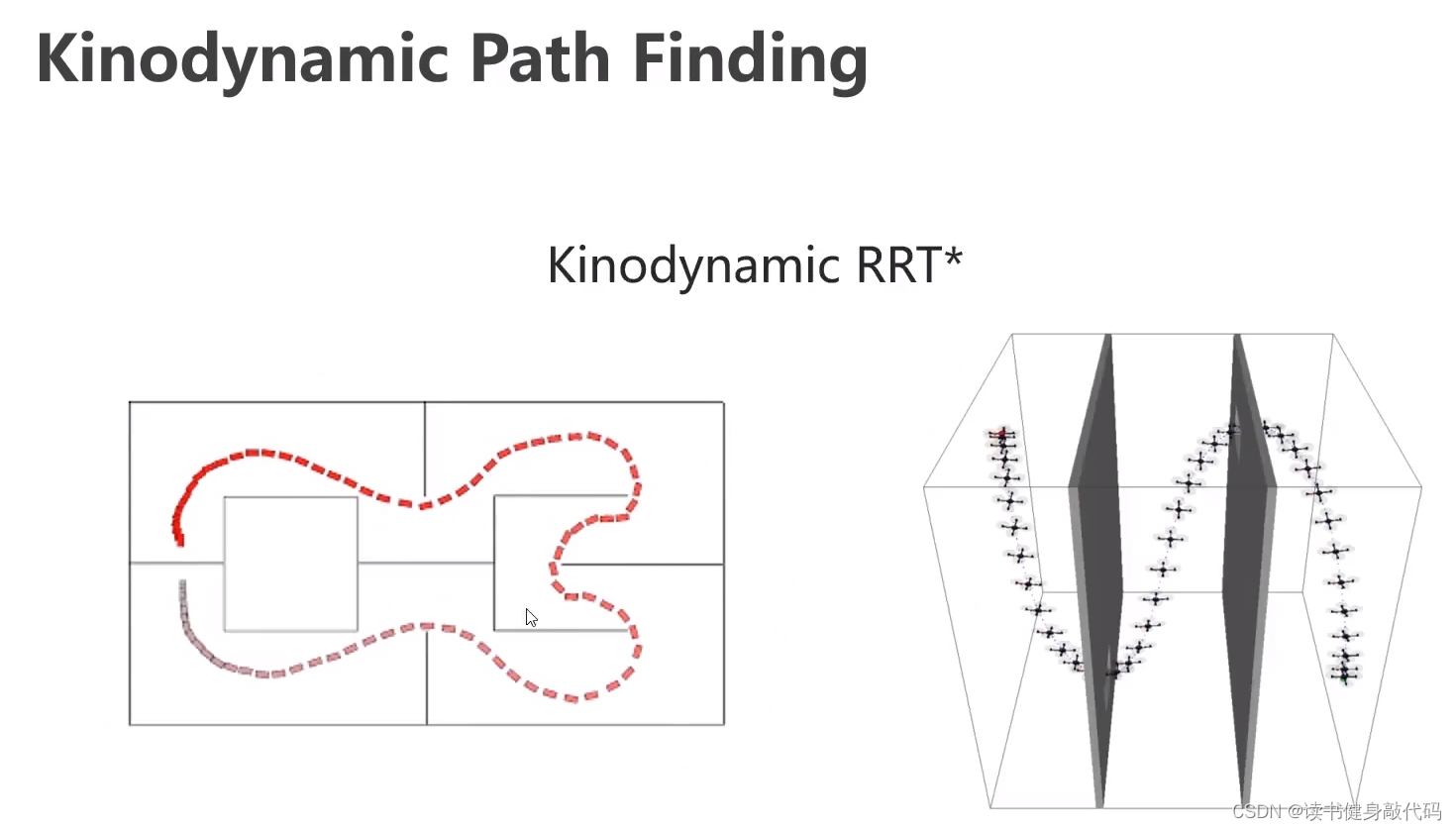
在这里插入图片描述

2. Kinodynamic RRT*
两点边界值的最优控制问题，现有边界，再计算中间的路径，和latice search相反，latice search是现有中间的路径集合，再计算最优终点。
在这里插入图片描述

2.2.4 后端轨迹优化

Minimun snap要保持机器人消耗能量最小
在这里插入图片描述

路标点之间生层traj，如果产生了碰撞，则在两点之间重新去一个点，再生成轨迹，尽可能逼近前端的直线path。

3. 地图表示

在这里插入图片描述
地图由数据结构和融合方法构成，二者有区别。

3.1 Occupancy grid map占用栅格地图

最稠密
结构化
直接访问

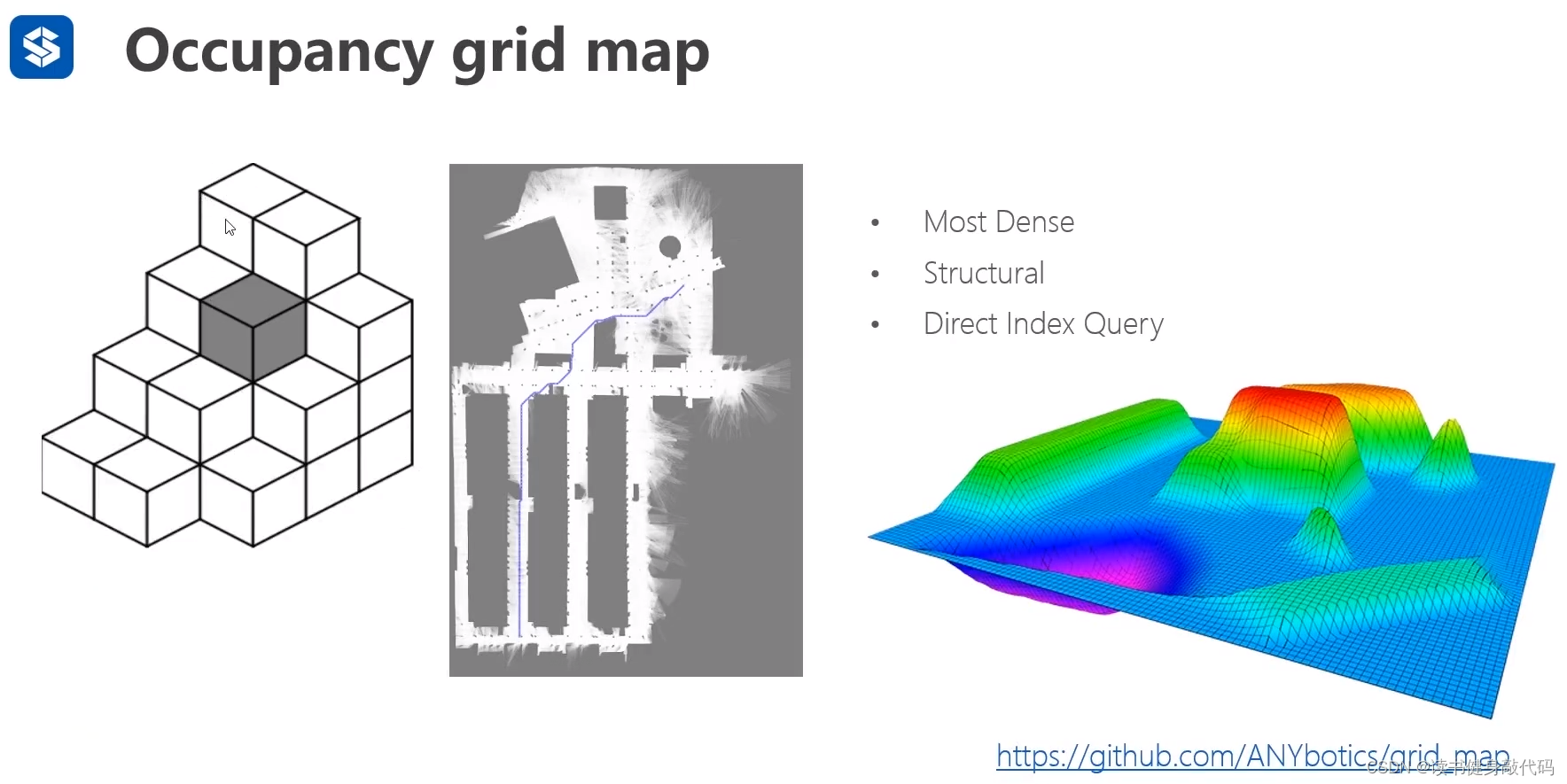
在这里插入图片描述
稠密
结构化

直接索引(O(1)复杂度)

https://github.com/ANYbotics/grid_map
这里安装不上grid map，说找不到costmap_2d，解了一会儿没解决，先放着。

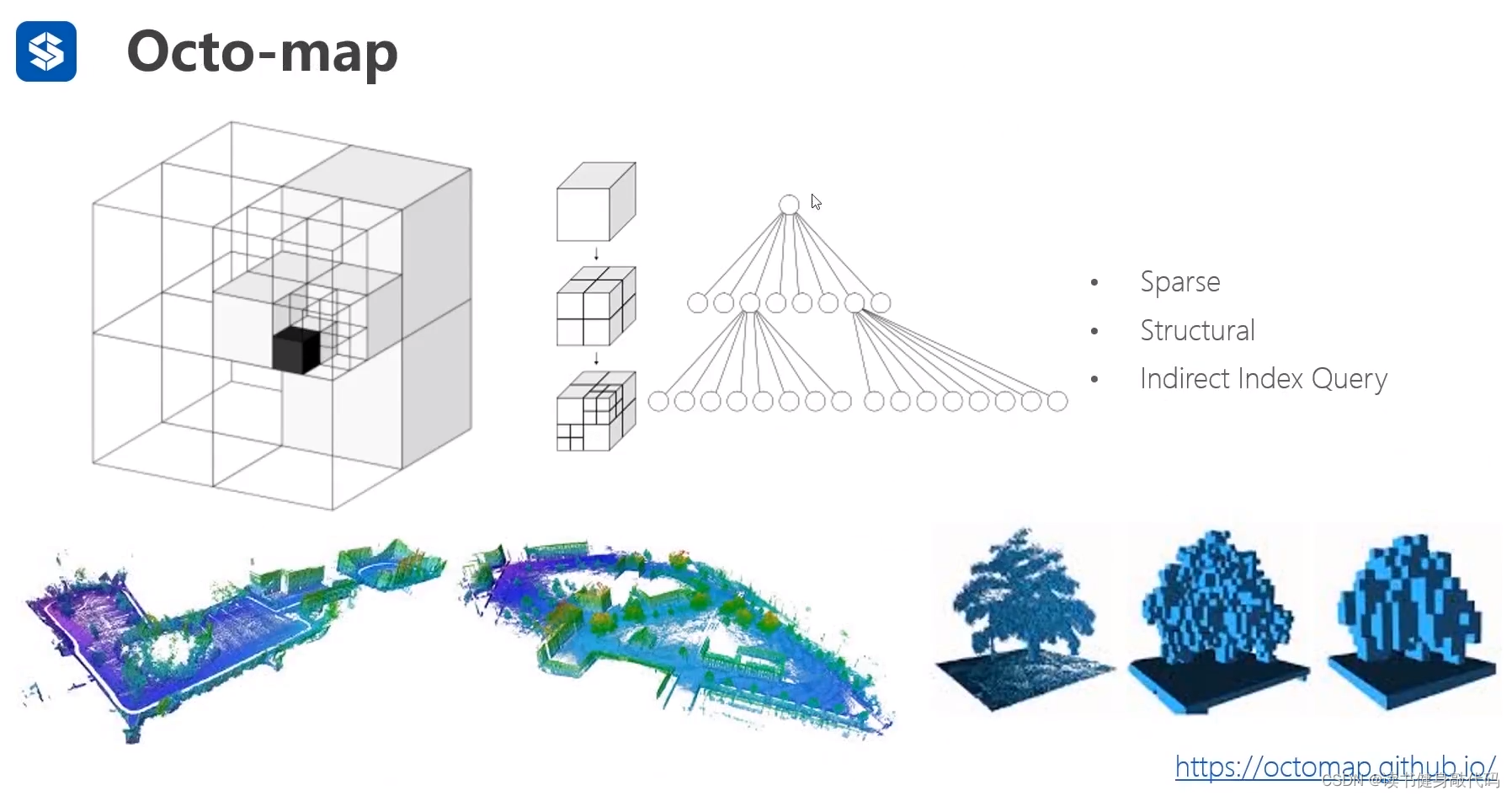
3.2 八叉树地图

稀疏
结构化
间接访问

https://octomap.github.io/

occupancy grid map虽然快，但是占用内存极大，为了减小内存占用，牺牲一定的查询速度，引入了八叉树地图，对于有障碍物的节点可以继续展开，没有的可以无需展开，但是访问障碍物需要通过父节点进行访问，速度比occupancy grid map慢，但内存占用少。
在这里插入图片描述

3.3 Voxel hashing（体素哈希）

最稀疏
结构化
间接访问

https://github.com/niessner/VoxelHashing
http://www.robots.ox.ac.uk/~victor/infinitam/
用在稠密重建或者3D SLAM上。
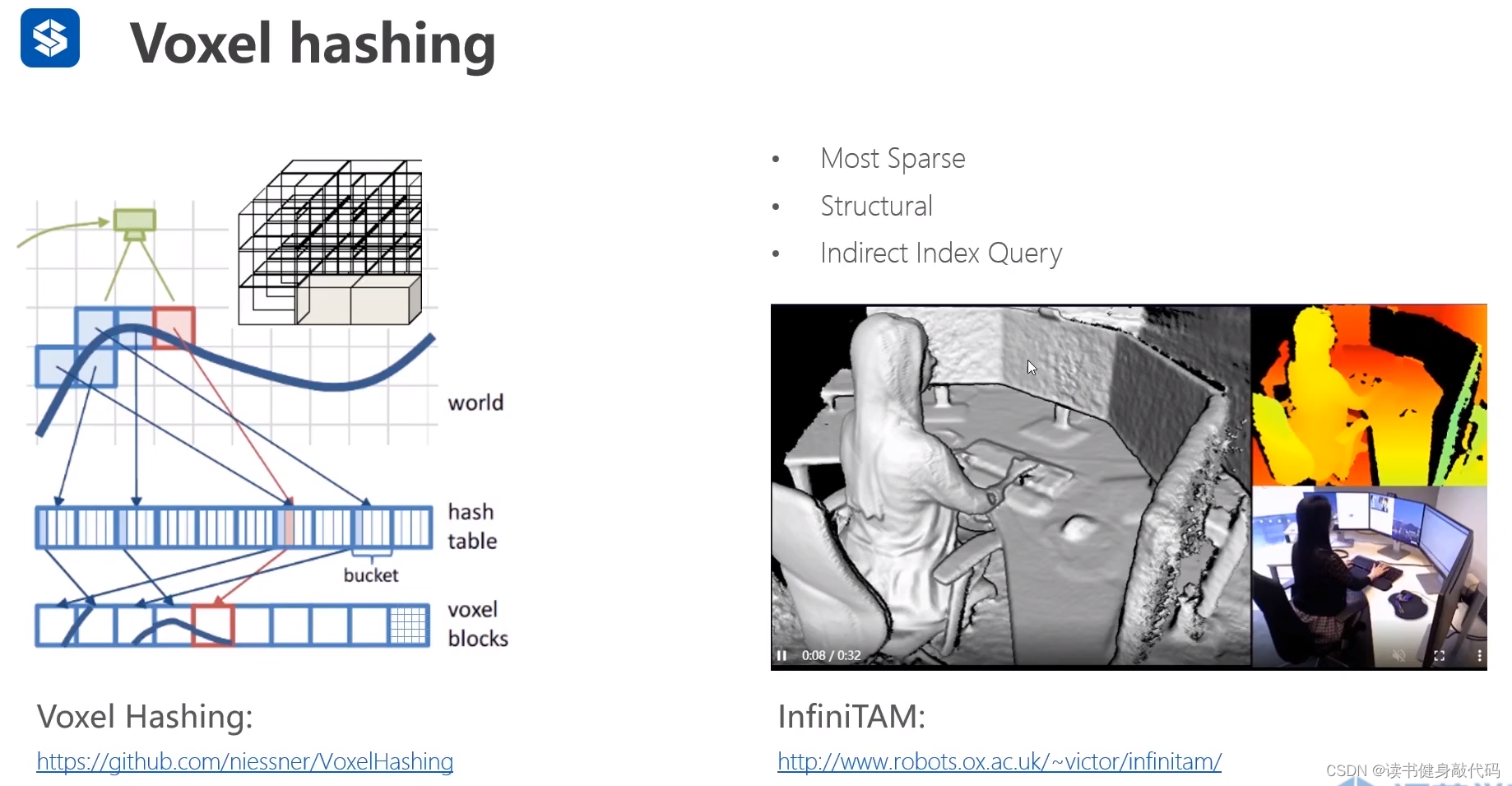
在这里插入图片描述
同样也是基于八叉树的数据结构，引入了block(图中555的大方格)和voxel(最小的方格)的概念，最终数据存放在每个voxel内，把每个block通过hash表的形式存储起来（具体为什么是最稀疏的目前还不了解）。

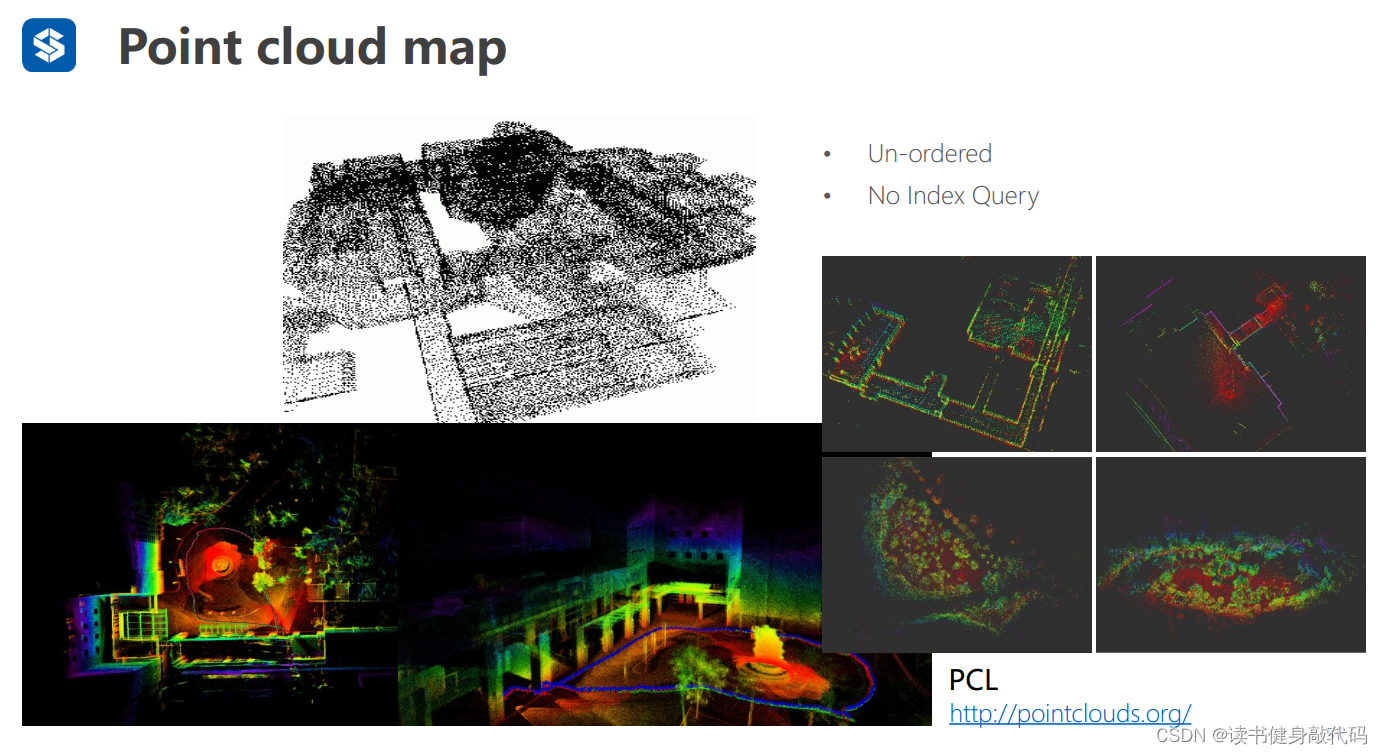
3.4 piint cloud点云

无序的
无索引查询

http://pointclouds.org/
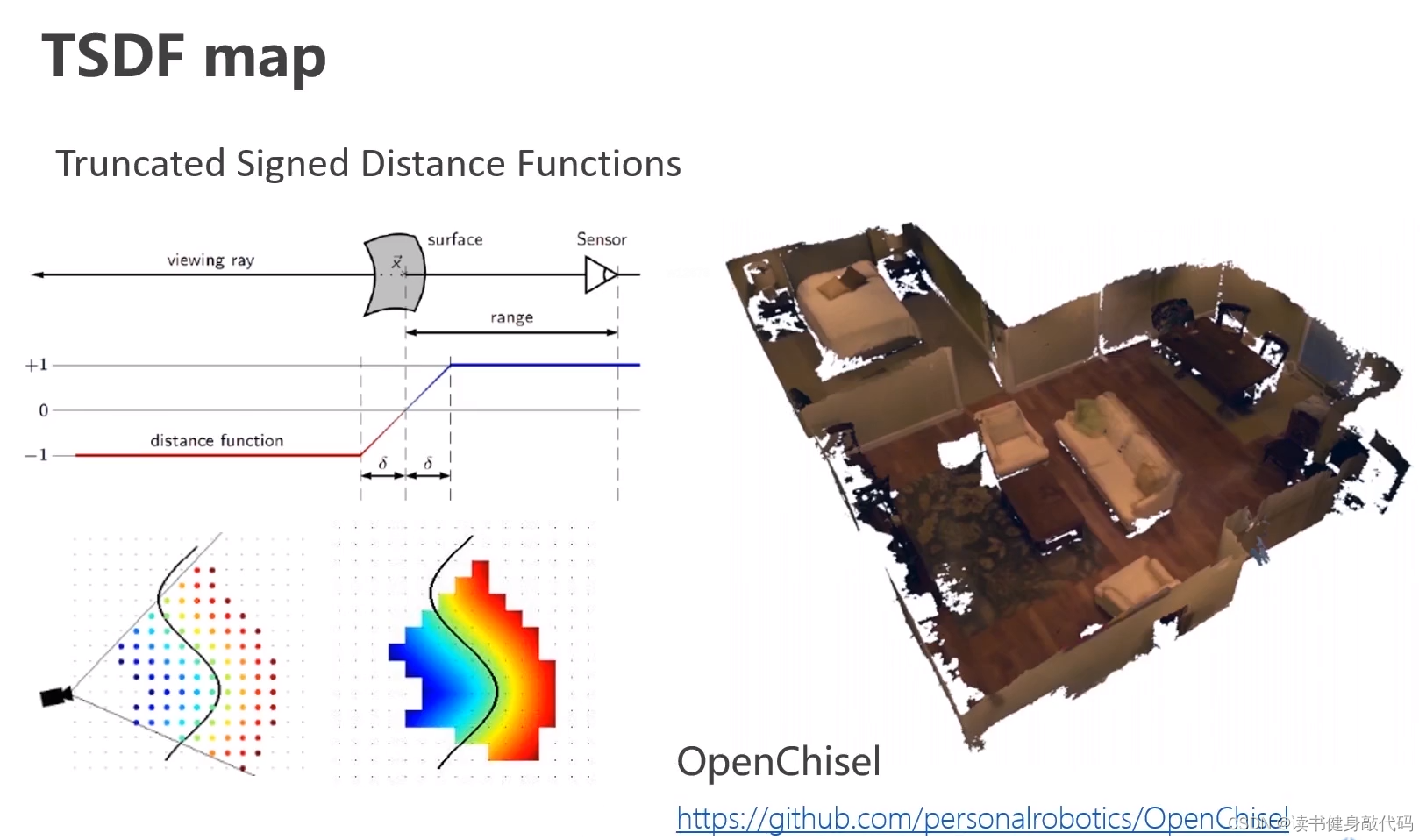
在这里插入图片描述

3.5 TSDF 截断符号距离函数

老规矩，还是叫TSDF地图，不翻译。voxel内存储的是该小块与距其最近的物体表面的距离。(可用GPU进行并行加速)
阶段的意思即只关心它的FOV内的一定距离的观测，剩下的截断不管。（ESDF则关心所有的，不进行截断）
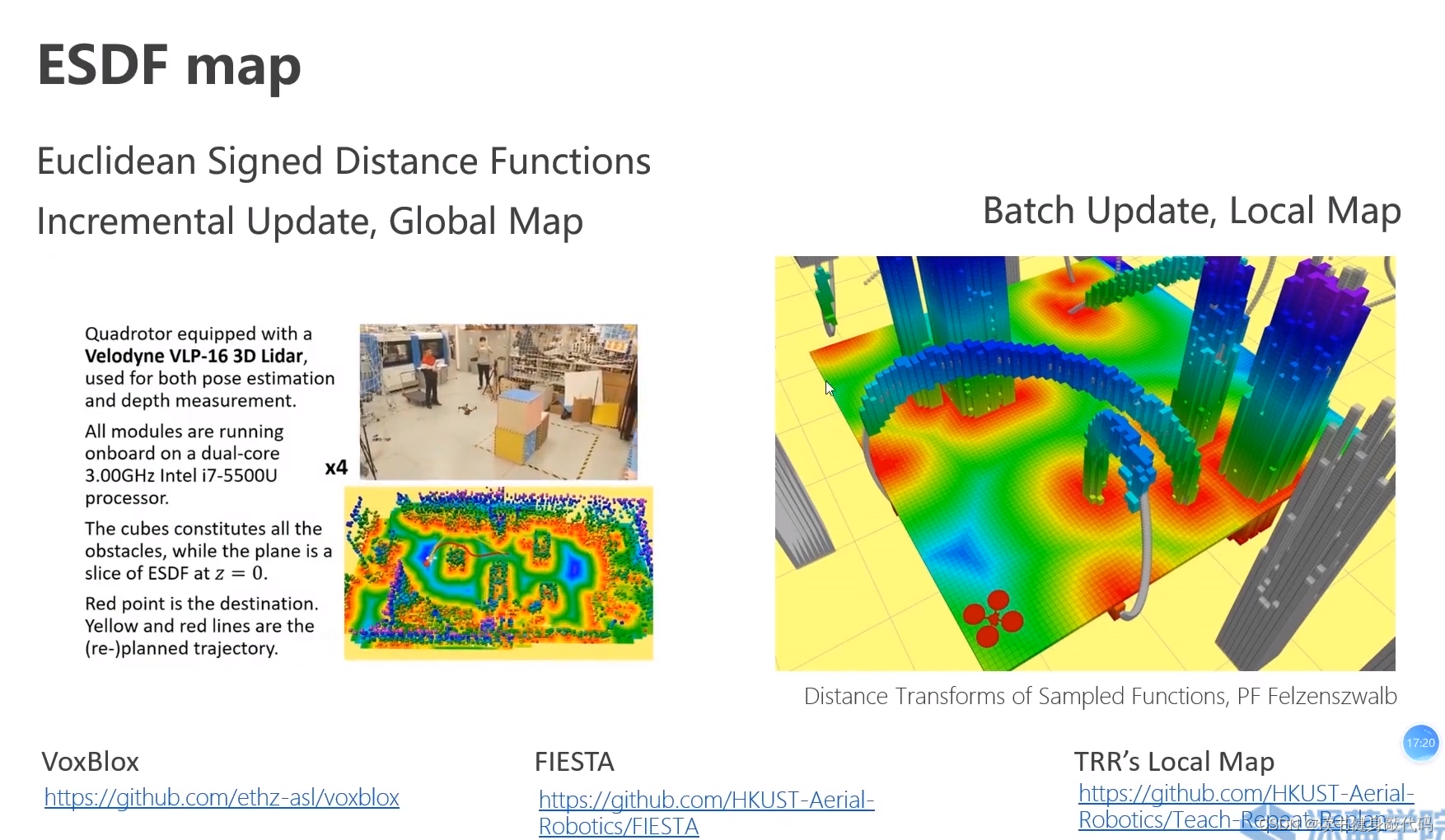
在这里插入图片描述

3.6 ESDF欧式符号距离函数

https://github.com/ethz-asl/voxblox
https://github.com/HKUST-Aerial-Robotics/FIESTA
https://github.com/HKUST-Aerial-Robotics/Teach-Repeat-Replan
对FOV内所有的观测都计算距离，目的是为了让生成的轨迹尽可能远离障碍物，提高安全性，思路是使用距离障碍物距离的梯度信息把轨迹往远离障碍物的地方推，如下图所示是高飞phd期间在港科大的工作：FIESTA和TRR‘s local map(teach repeat replan). 均基于ESDF
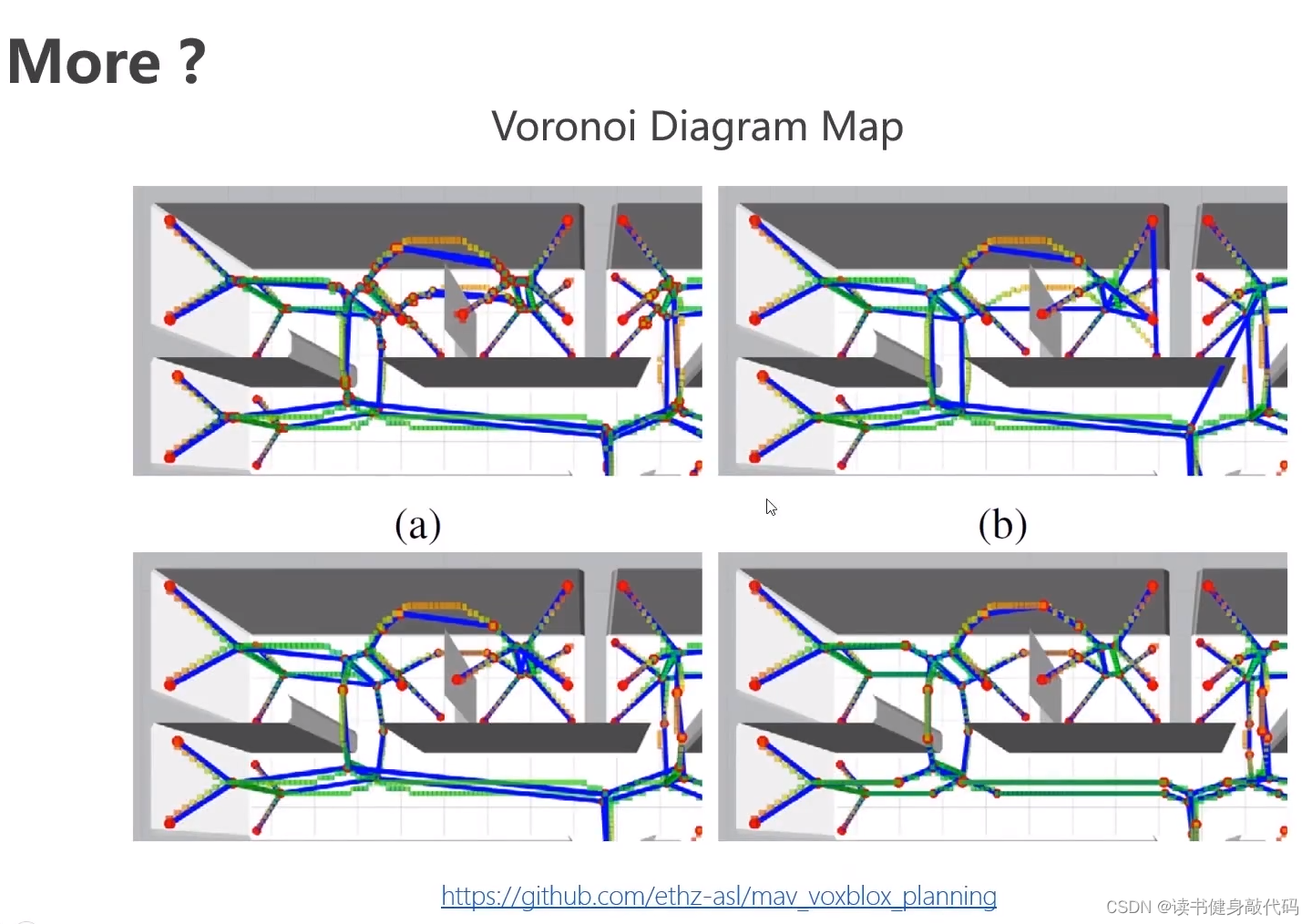
在这里插入图片描述

3.7 More

在这里插入图片描述
蓝色是障碍物，棕色是free space，用凸的多面体表示。（凸会带来很多好处，Ch4，5学完之后会了解。）

表示空间的拓扑结构，skeleton骨架，非常稀疏，速度也会很快。
在这里插入图片描述

4. Occupancy grid map

Fast-Planner和EGO-Planner(Ch8会讲)都使用了Occupancy grid map。

4.1 理论推导

推导参考文献[1]
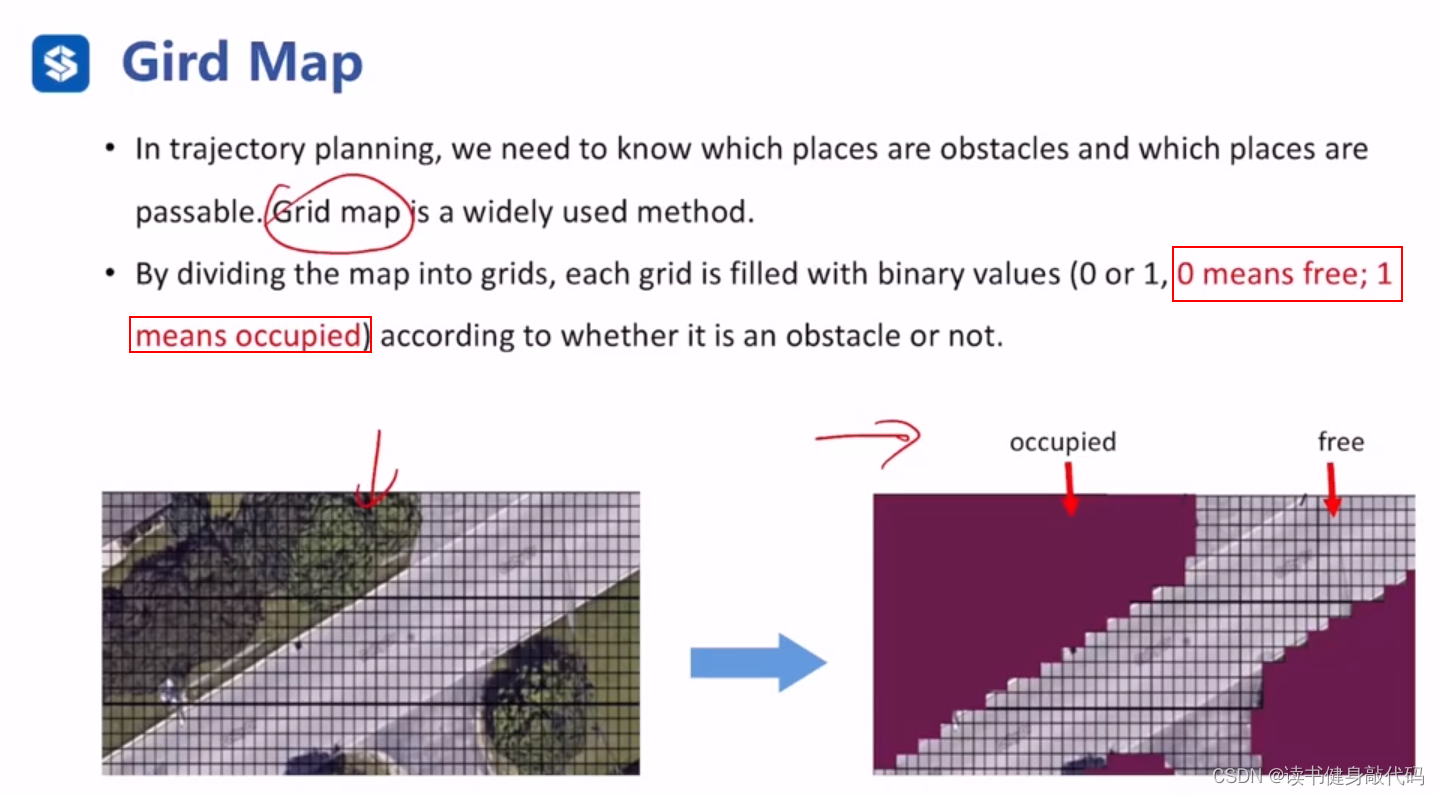
在这里插入图片描述
0代表free，1代表occupied，常是障碍物。

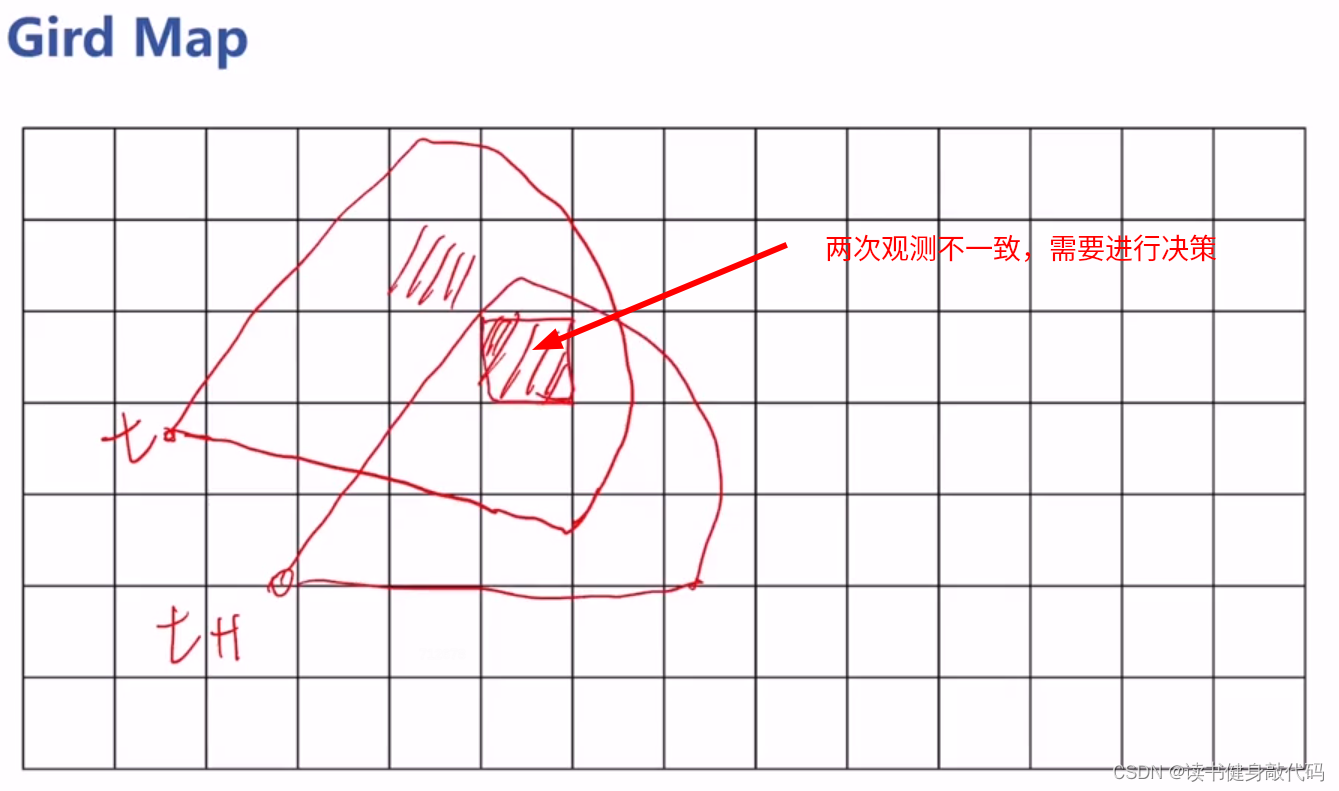
但是传感器观测是带噪声的，在某处观测为occupied在另一处为free，如何处理？

答：计算每个栅格的后验概率。

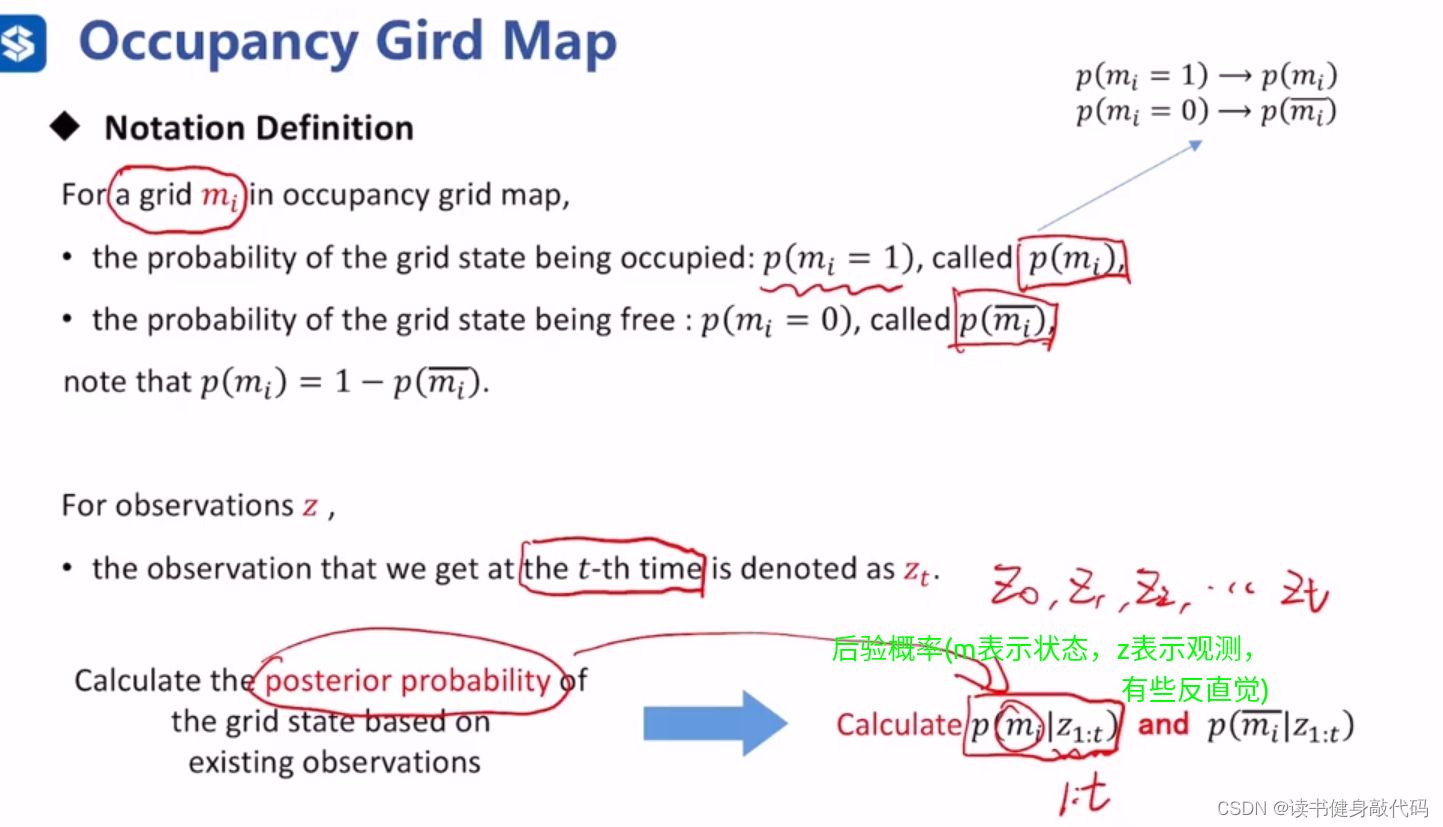
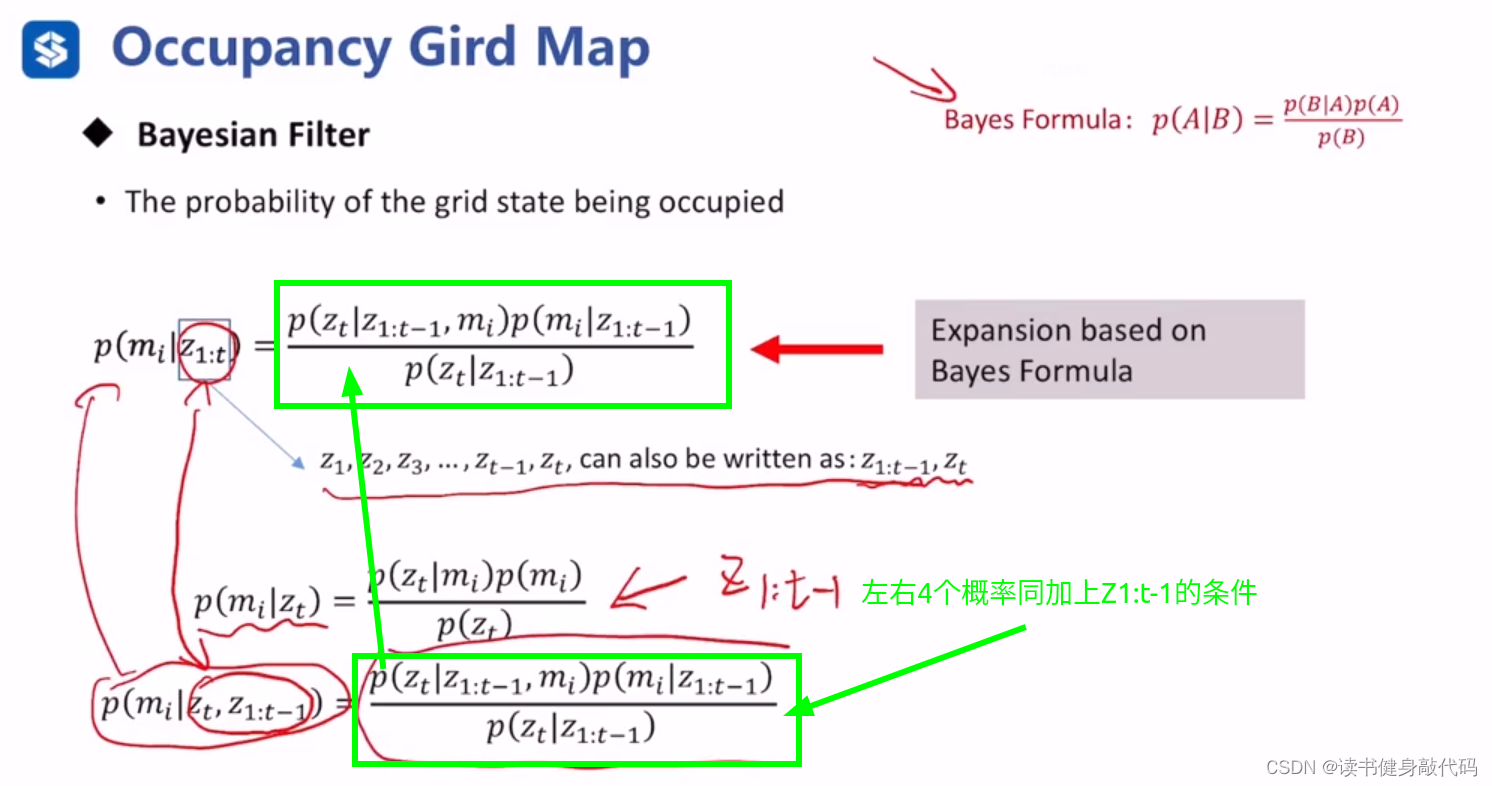
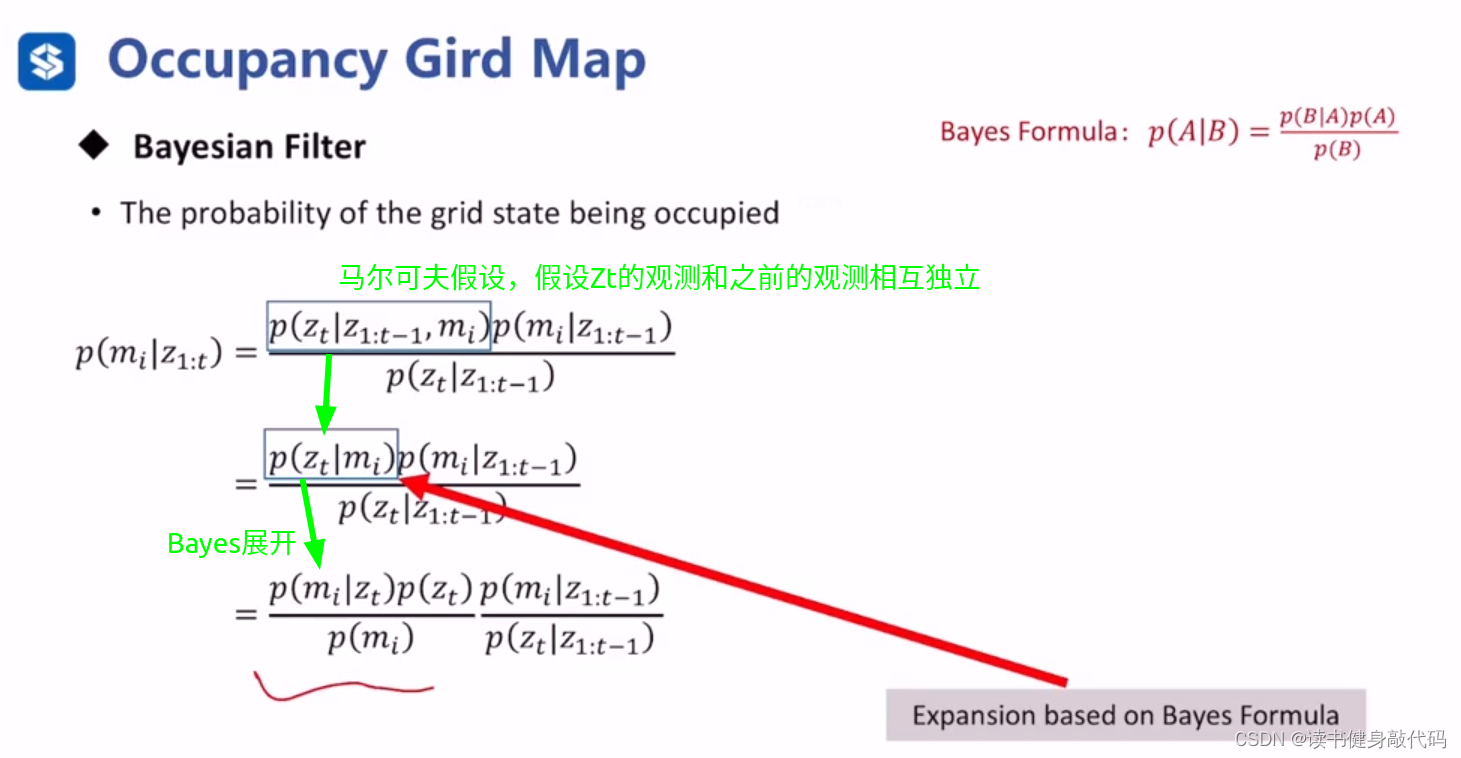
在这里插入图片描述

可以看出方框内的递推关系了。

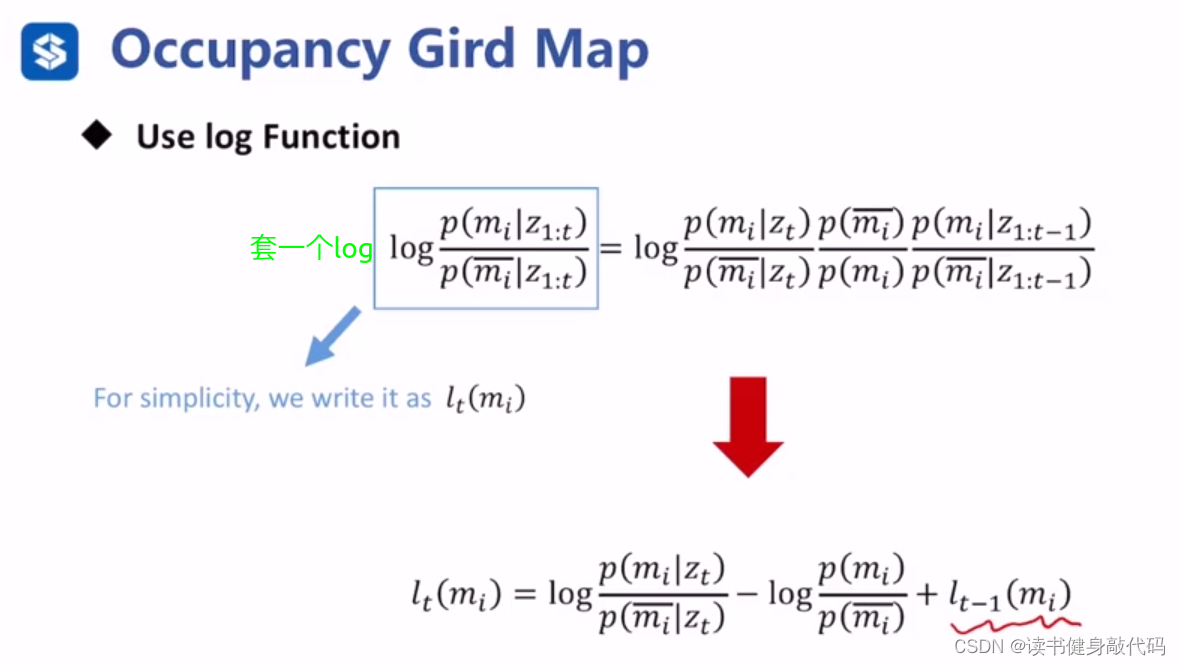
在这里插入图片描述
$l_{t}(m_i)$ 中涉及到逆传感器模型：

逆传感器模型使用bayes转为传感器模型：

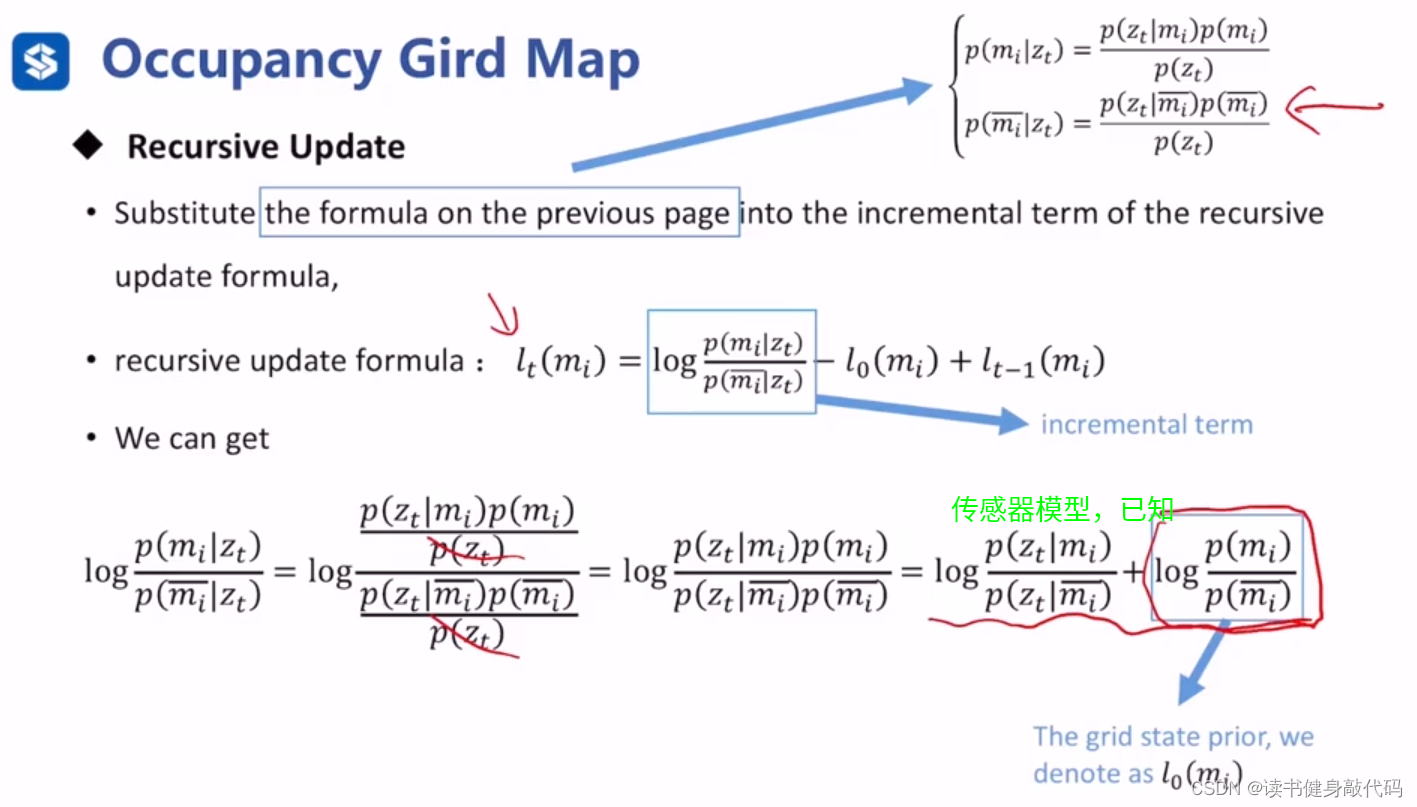
中间的一项 $log\frac{p(z_t|m_i)}{p(z_t|\overline{m_i})}$ 即为传感器模型相关，接下来进行讨论：

在这里插入图片描述

假设传感器的观测模型不变，即a和b的值不变，则我们对 $l_t(m_i)$ 进行更新只需简单的加减操作

在这里插入图片描述
上面讨论的是 $l_t(m_i)$ 的性质，我们最开始是要讨论后验概率 $p(m_iz_{1:t})$ ，这二者有什么关系？

实际上可以使用 $l_t(m_i)$ 的正负来代替后验概率来判断状态 $m_i$ ，假设我们求出了后验概率 $p(m_iz_{1:t})$ ，那我们可以设置一个阈值0.5，

当 $p(m_iz_{1:t})>0.5$ ，我们认为 $m_i=1$ ，
反之 $m_i=0$ ，

使用 $l_t(m_i)$ 则
当 $l_t(m_i)>0, m_i=1$
反之 $m_i=0$

以上即为occupancy grid map的结论。

那么为何 $l_t(m_i)$ 能替代后验概率呢？需要对 $l_t(m_i)$ 的函数性质进行讨论，记后验概率 $p(m_iz_{1:t})=x$ ，有以下讨论：

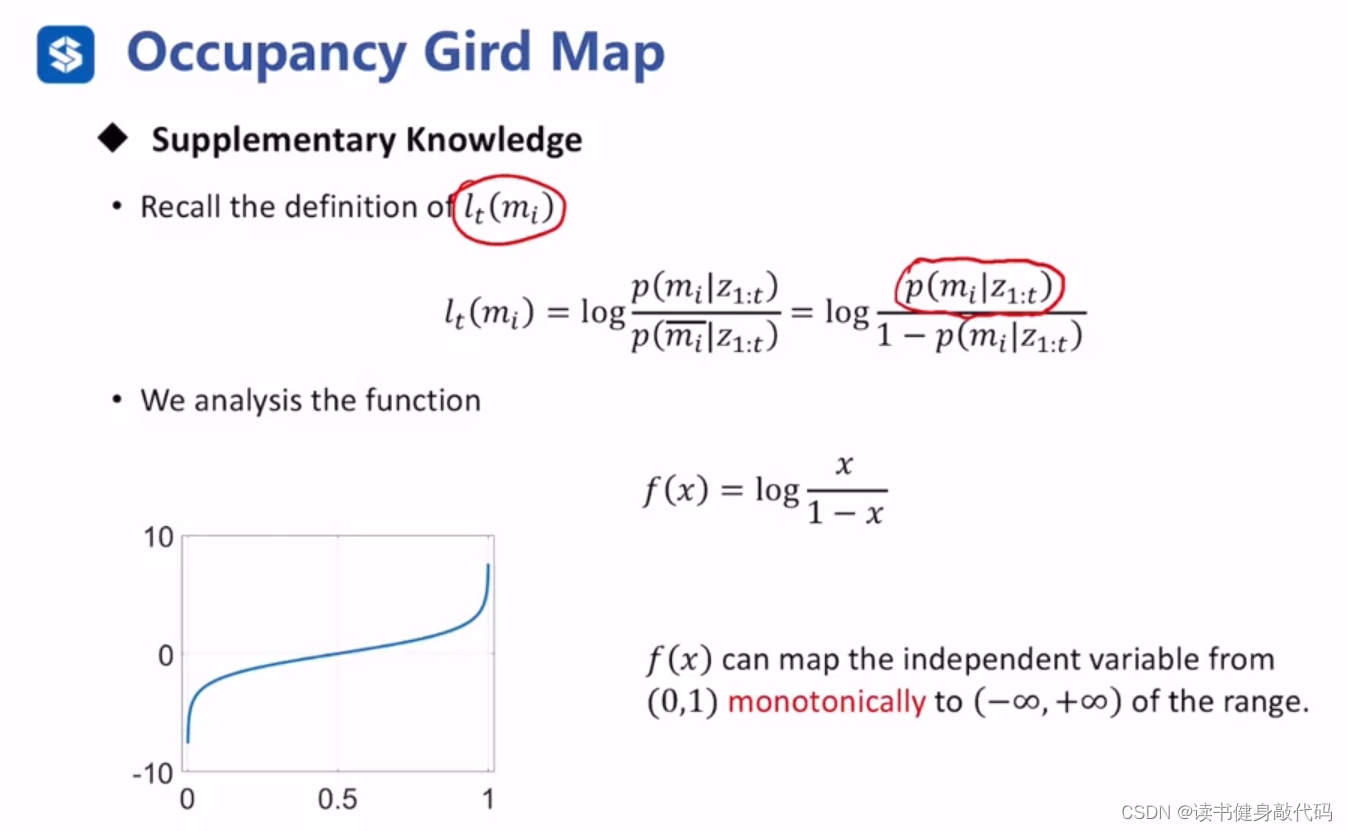
在这里插入图片描述

4.2 occupancy Grid Map小结

在这里插入图片描述

5. Euclidean Signed Distance Field(ESDF)

5.1 计算步骤

参考文献[2]
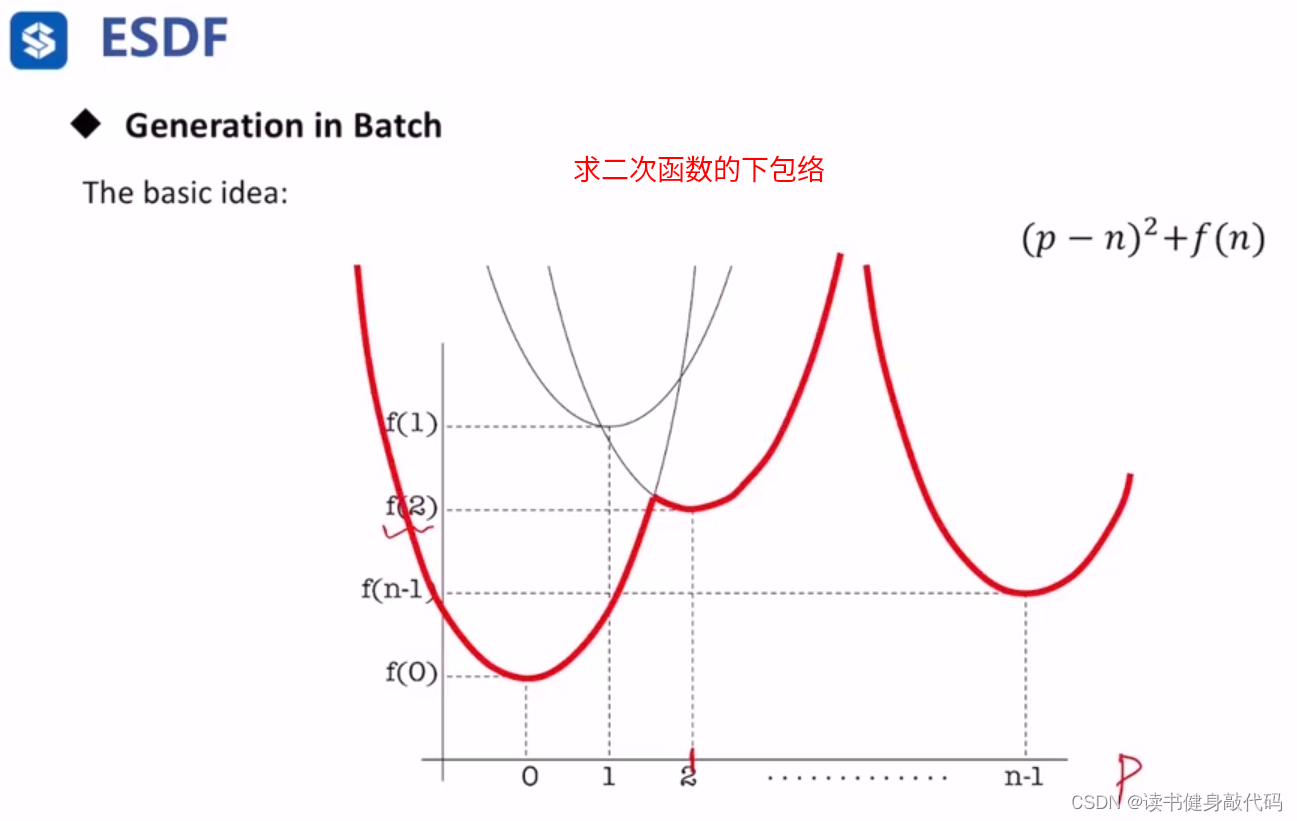
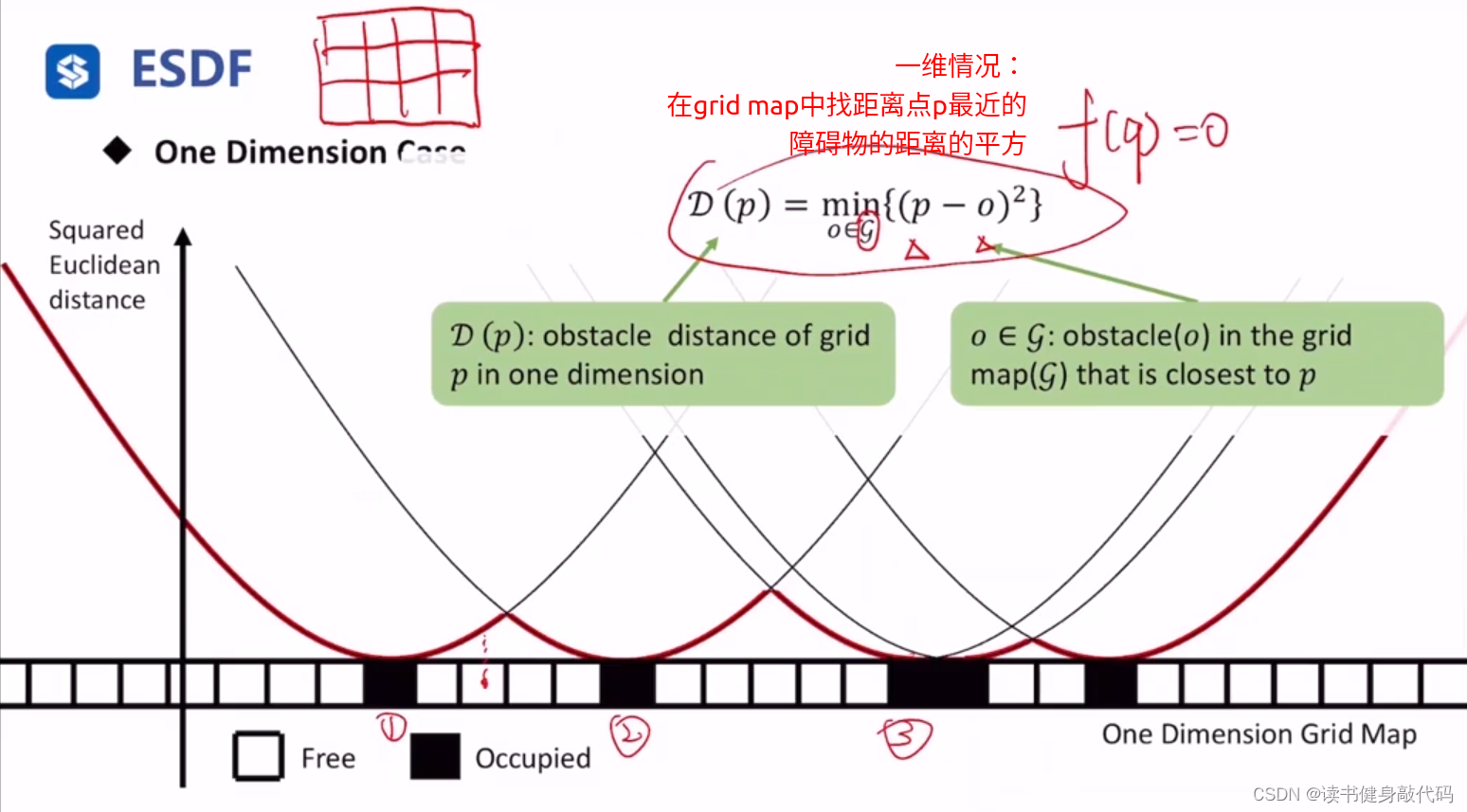
在这里插入图片描述

在这里插入图片描述

关于采样函数q，对于高维ESDF有用

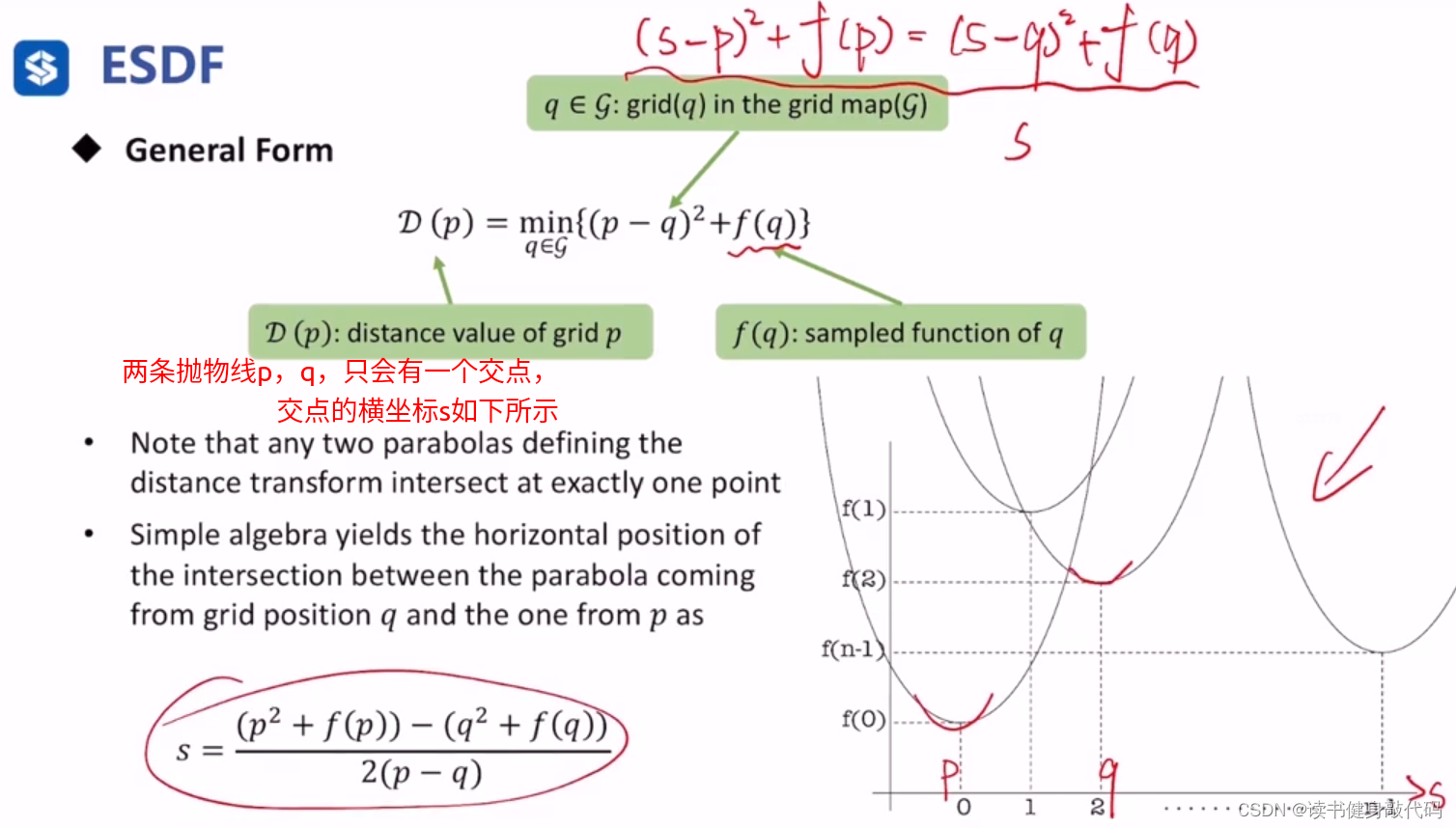
在这里插入图片描述

一维ESDF的计算伪代码：

算法逻辑比较绕，此处不进行展开。
在这里插入图片描述
y与x无关，所以可以fix一项变为一维形式，求另一项

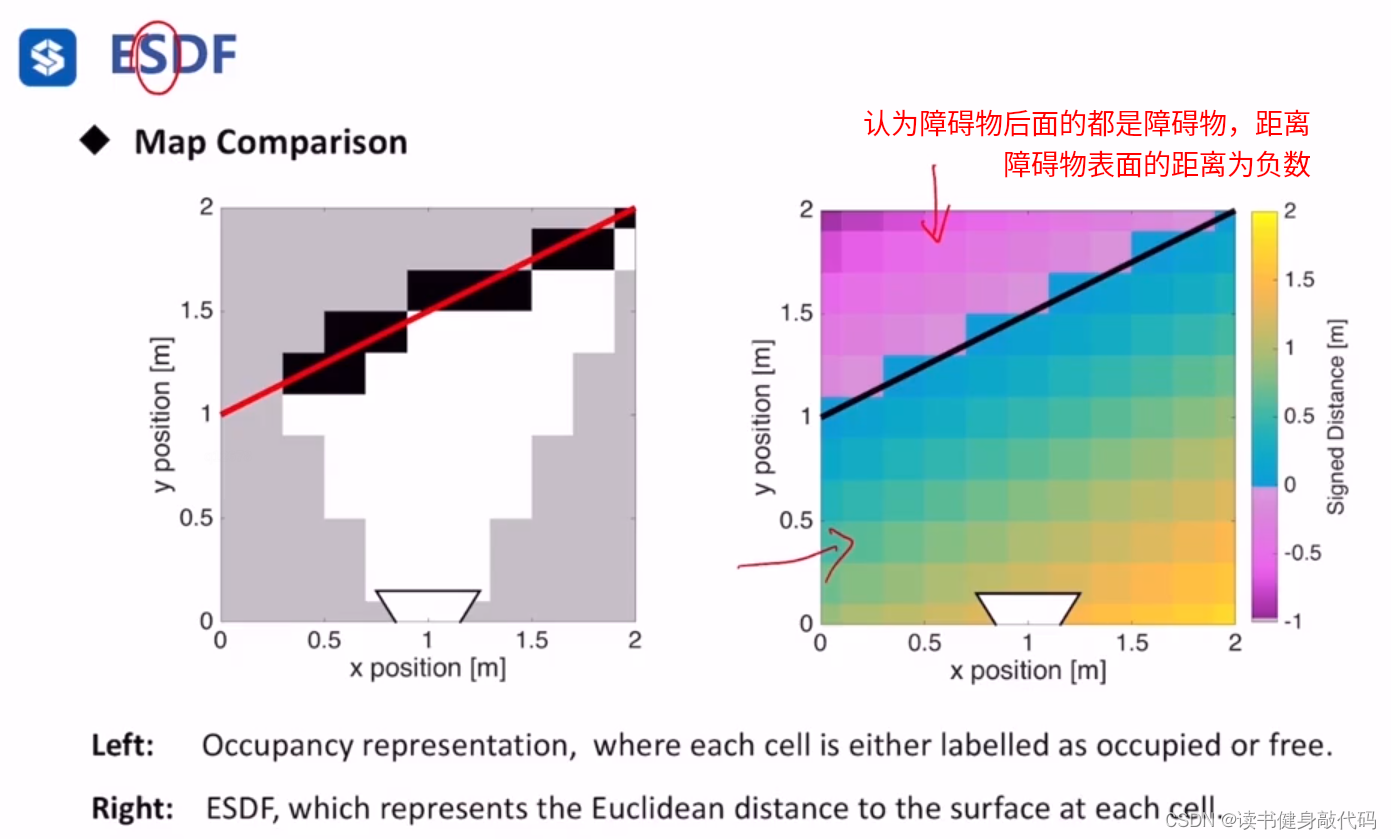
ESDF物理意义：

没有障碍物就认为障碍物在无穷远，距离是 $\infty$

只管y相关的项，计算离最近障碍物的距离的平方 $d_1$ (调用上述伪代码计算1维ESDF值)
fix x，遍历x’的值，计算距离平方，加上 $d_1$ 即为 $D$

只管y相关的项：
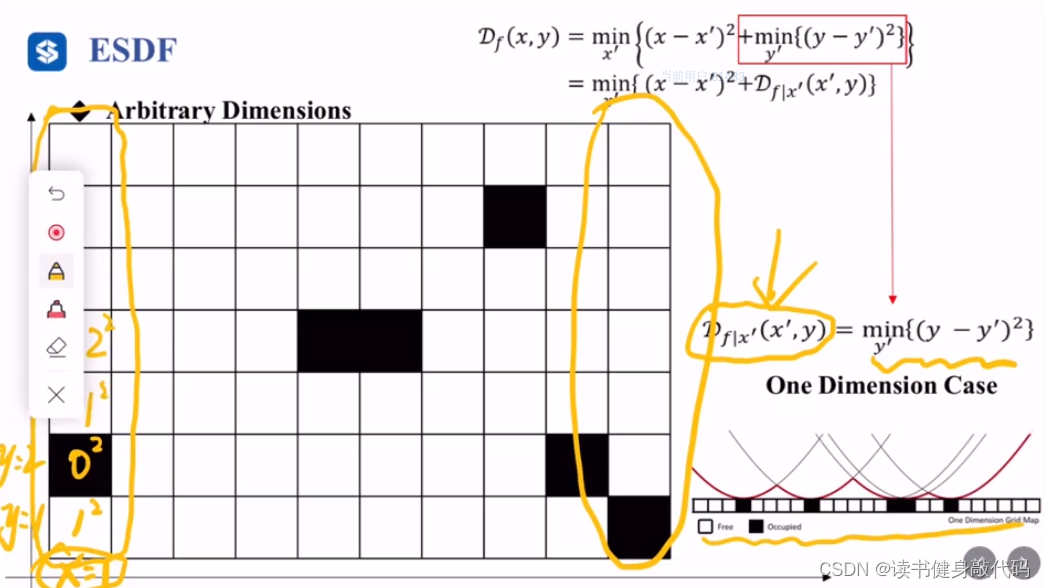
在这里插入图片描述
2. 将d1当做常量，固定x的值，eg： $x = 1$ ，变化 $x^ \prime$ 的值，计算 $(x-x^\prime)^2+d_1$ ，

障碍物里面存放的值是到最近的free栅格的距离，是负值。
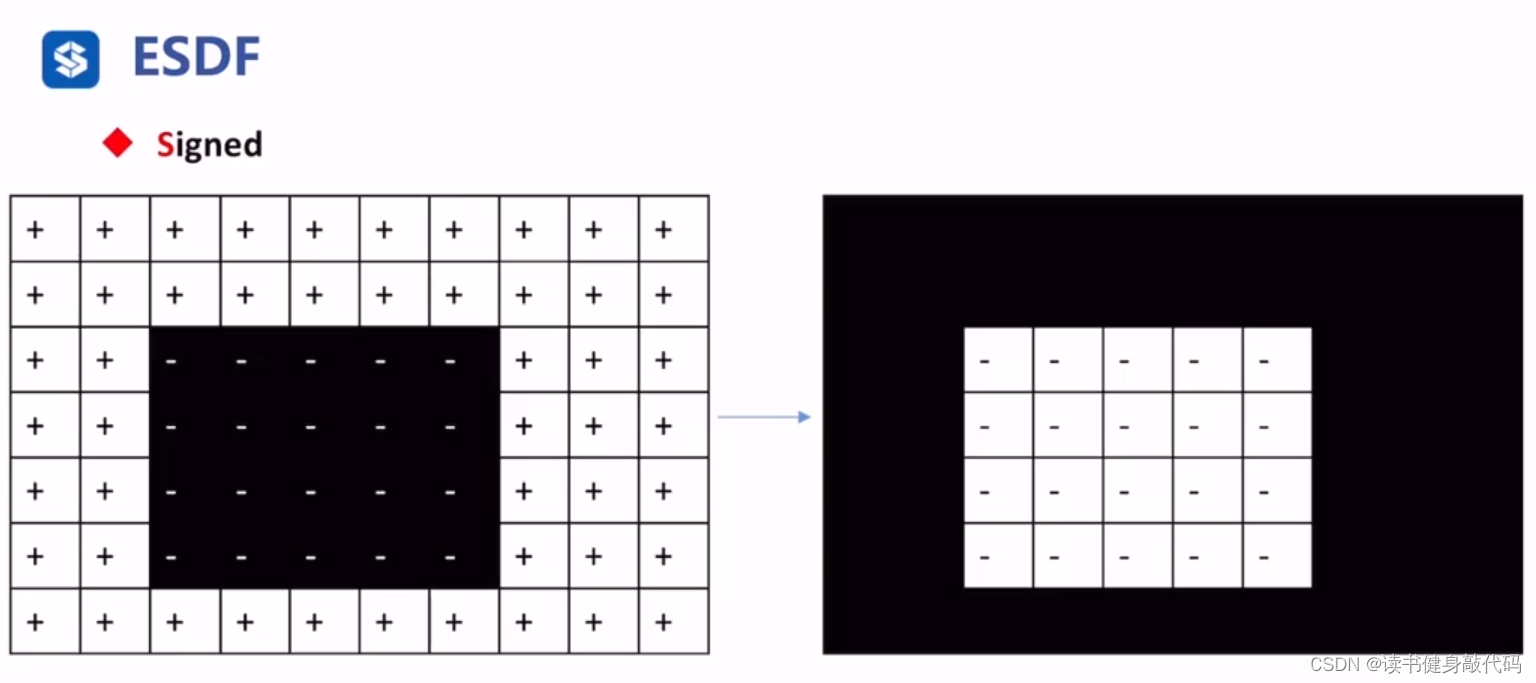
在这里插入图片描述

5.2 ESDF代码

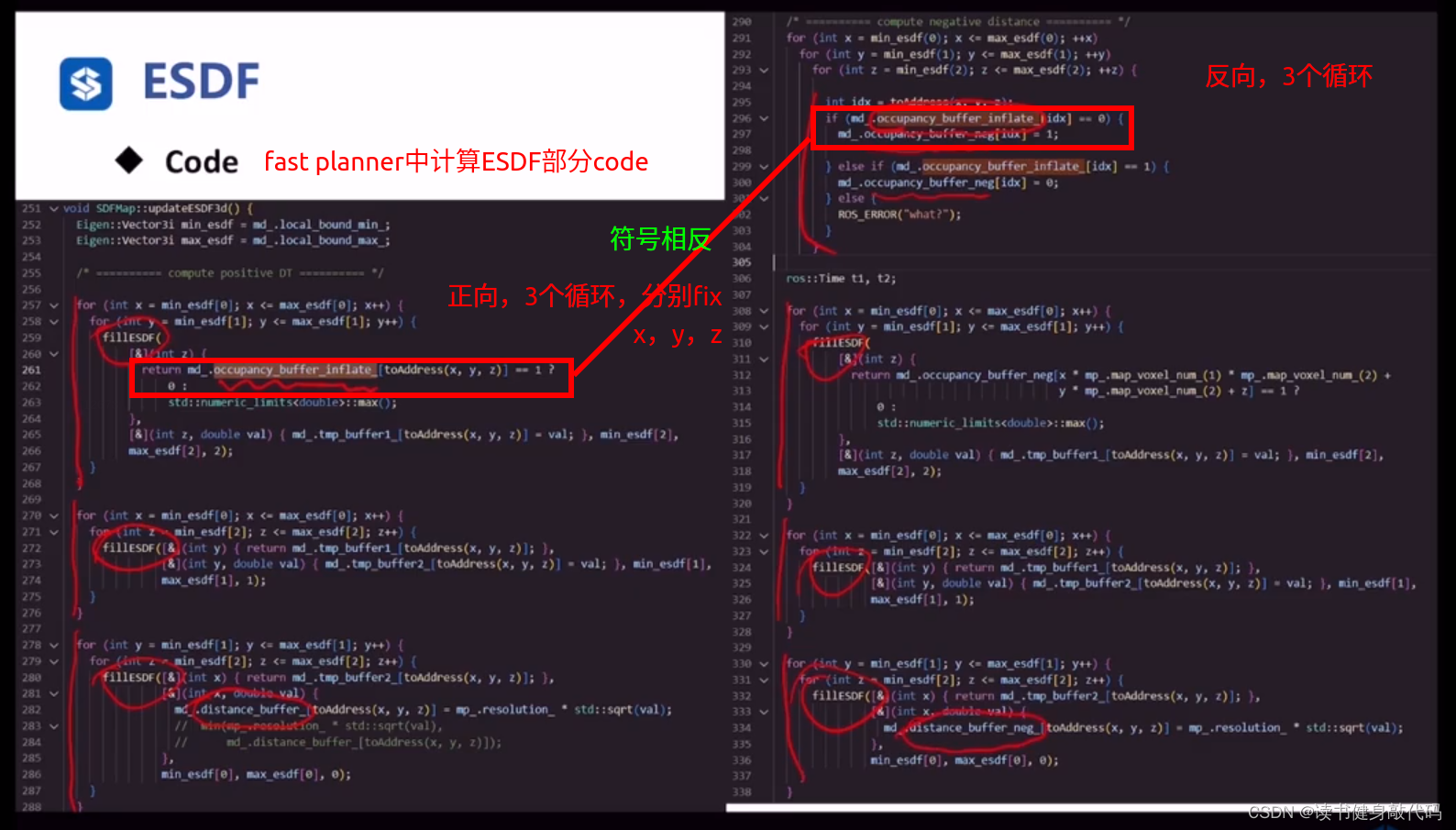
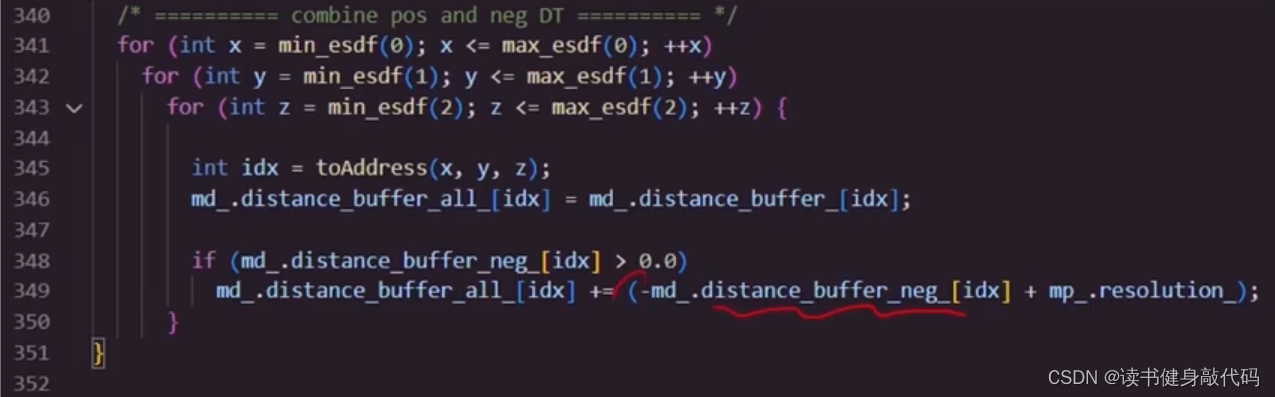
在这里插入图片描述

5.3 线性插值及梯度计算

当不在栅格点正中间，需要对点进行插值，如下为一维和二维情况：

线性插值(2点)与双线性插值(4点)
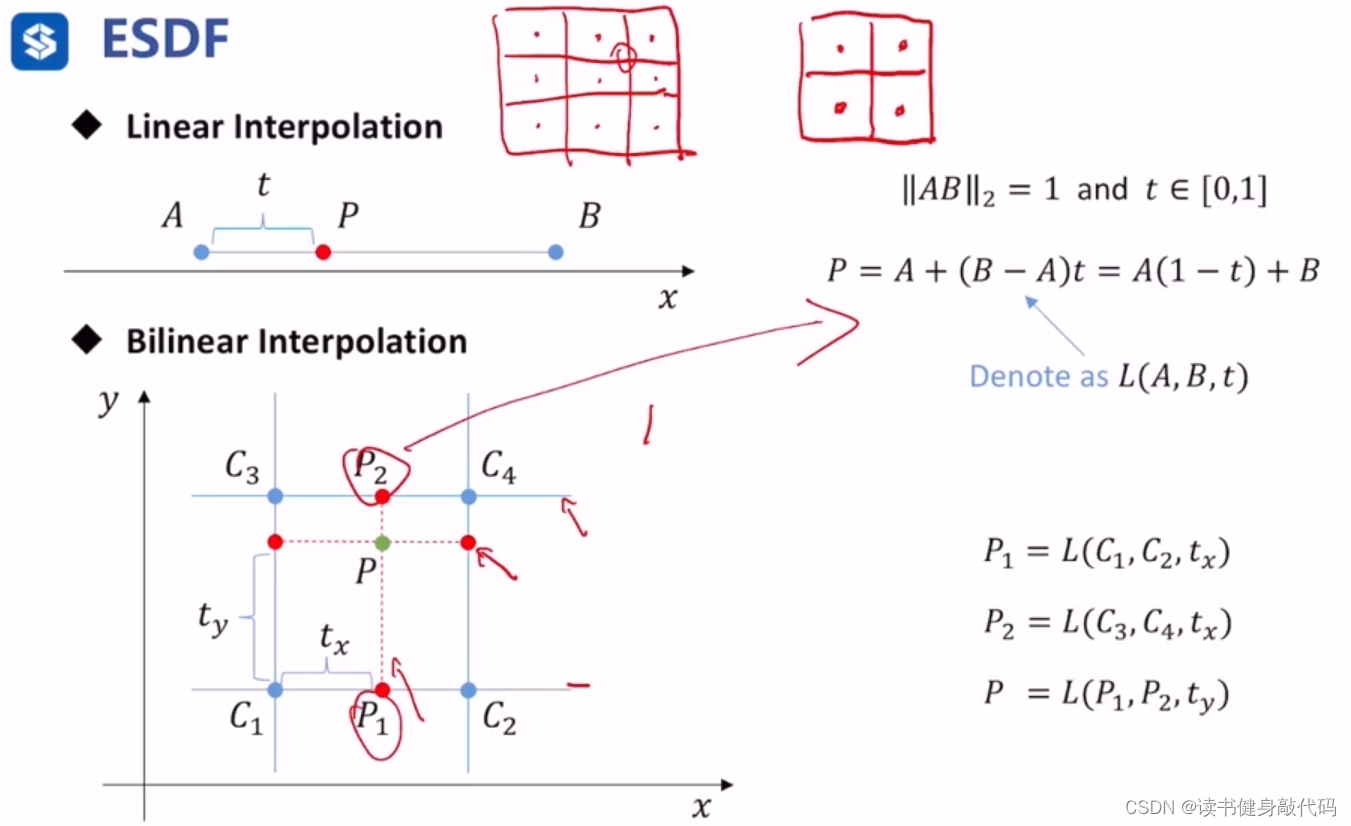
在这里插入图片描述

三维情况：三线性插值（8个点）
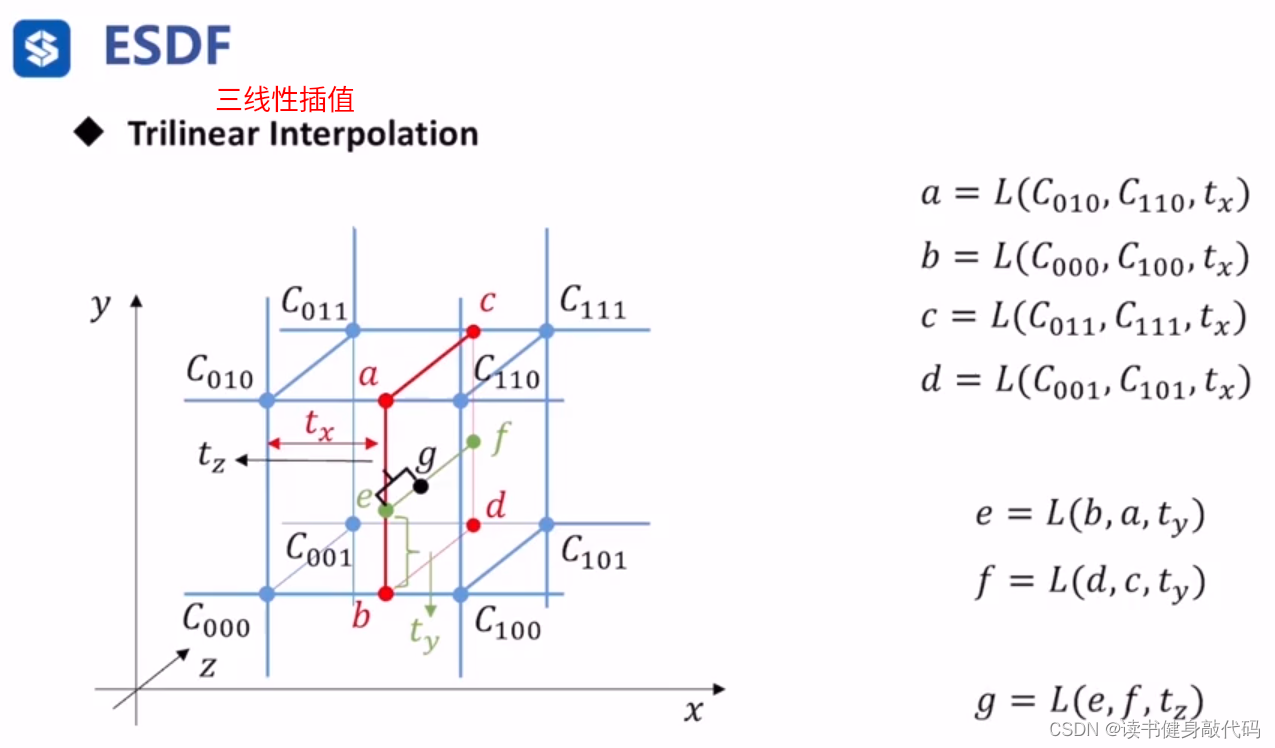
在这里插入图片描述

前面讲到ESDF可以使用梯度来使得轨迹更远离障碍物，更安全，如果不在栅格中心，梯度的计算也依赖于线性插值，以下为3维情况：
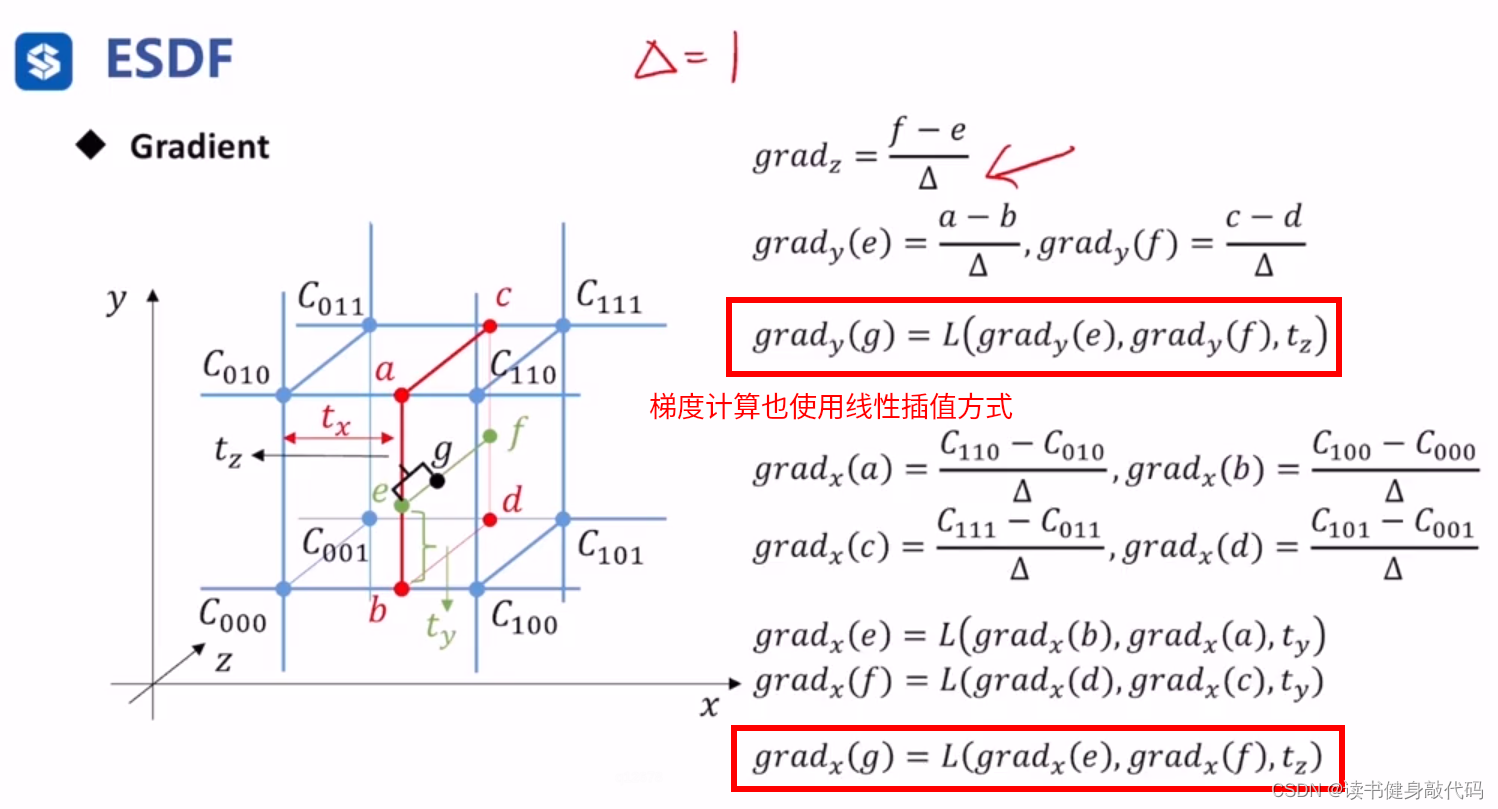
在这里插入图片描述

课程着重于算法原理的讲解，如果要想了解实现，强烈建议看Fast planner的源码，跑通他们的例程，有条件的可以使用传感器采集bag包，跑他们的建图程序。

6. Refernece

[1] https://www.cs.cmu.edu/~16831-f14/notes/F14/16831_lecture06_agiri_dmcconac_kumarsha_nbhakta.pdf
[2] Felzenszwalb, Pedro F., and Daniel P. Huttenlocher. “Distance transforms of sampled functions.” Theory of computing 8.1 (2012): 415-428.