题目描述
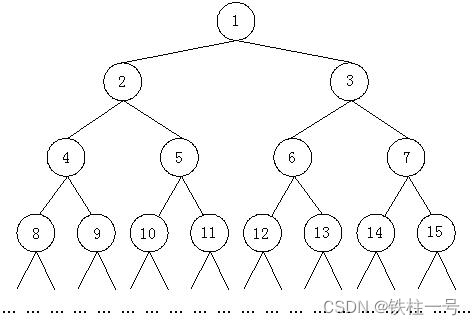
如上图所示,由正整数1, 2, 3, ...组成了一棵无限大的二叉树。从某一个结点到根结
点(编号是1 的结点)都有一条唯一的路径,比如从10 到根结点的路径是(10, 5, 2, 1),
从4 到根结点的路径是(4, 2, 1),从该结点到根结点的路径上的所有结点称为该结点的祖先。现在的问题就是,给定x 和y,求x和y的最近共同祖先,比如,10和4最近共同祖先是2,10和5的最近共同祖先是5。
定义递归函数
int common(int x, int y)
{
如果x==y, return x;
如果x>y,求x/2与y的共同祖先;
否则,求x与y/2的共同祖先;
}
输入
输入只有一行,包括两个正整数x 和y,这两个正整数都不大于1000。
输出
输出只有一个正整数,即x和y的最近共同祖先。
样例输入 Copy
10 4
样例输出 Copy
2
源代码
#include <stdio.h>
int common(int x,int y);
int main()
{
int x,y;
scanf("%d %d",&x,&y);
printf("%d",common(x,y));
return 0;
}
int common(int x,int y)
{
if(x==y)
{
return x;
}
if(x>y)
{
return common(x/2,y);
}
if(x<y)
{
return common(x,y/2);
}
}