题目所属分类

从右上角出发往下遍历倒是也可以二分

原题链接

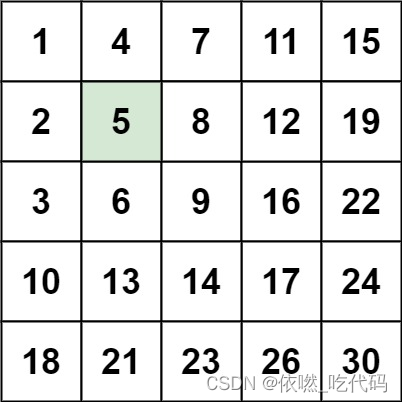
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

代码案例：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

题解

从右上角出发，初始化i = 0,j = m - 1

1、若matrix[i][j] == target，返回true
2、若matrix[i][j] > target，向左走，j --
3、若matrix[i][j] < target，向下走，i ++
4、如果出界，返回false
时间复杂度O（n + m ）

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int n = matrix.length ;
        int m = matrix[0].length ;
        if(n == 0 || m == 0) return false;
        int i = 0 , j = m -1 ;
        while(i <  n && j >= 0){
            int t = matrix[i][j] ;
            if(t == target) return true;
            if(t < target) i ++ ;
            else j-- ;
        }
        return false ;
    }
}

还可以二分
二分

枚举每一行，由于每一行都是升序的，对每一行通过二分找到小于等于 target 的最大值，若存在某一行中matrix[i][l] == target，则直接返回true，否则返回false

时间复杂度 O(nlogm)

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if(matrix.length == 0 || matrix[0].length == 0) return false;
        int n = matrix.length;
        int m = matrix[0].length;
        for(int i = 0;i < n;i ++)
        {
            int l = 0, r = m - 1;
            while(l < r)
            {
                int mid = l + r + 1 >> 1;
                if(matrix[i][mid] <= target) l = mid;
                else r = mid - 1;
            }
            if(matrix[i][l] == target) return true;
        }
        return false;
    }
}