扩展欧几里得算法总结

news2025/10/31 22:58:55

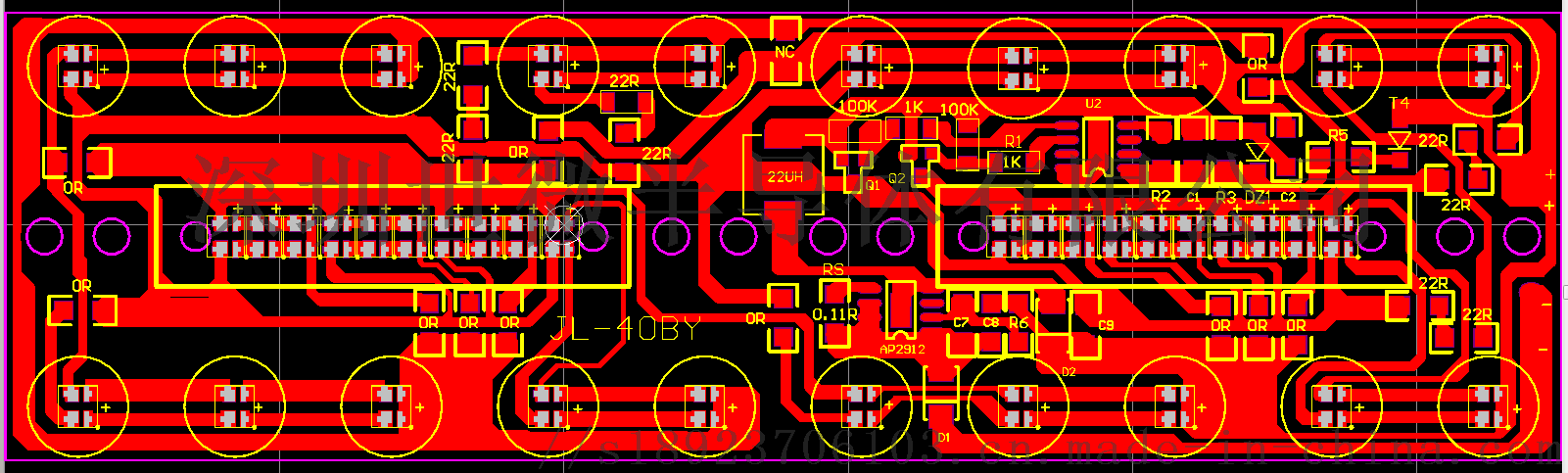
知识概览

裴蜀定理：对于任意正整数a，b，一定存在非零整数x，y，使得

$ax + by = (a,b)$

而且(a, b)是a和b能凑出来的最小的正整数。

通过扩展欧几里得算法可以求得裴蜀定理中x和y的值，x和y的通解为

$\left\{\begin{matrix} x = x_0 - \frac{b}{a} \cdot k\\ y = y_0 + \frac{b}{a} \cdot k \end{matrix}\right.$ ， $k\in \mathbb{Z}$

例题展示

扩展欧几里得算法

题目链接

活动 - AcWing 系统讲解常用算法与数据结构，给出相应代码模板，并会布置、讲解相应的基础算法题目。https://www.acwing.com/problem/content/879/

代码

#include <iostream>

using namespace std;

int exgcd(int a, int b, int &x, int &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    
    int d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

int main()
{
    int n;
    scanf("%d", &n);
    
    while (n--)
    {
        int a, b, x, y;
        scanf("%d%d", &a, &b);
        
        exgcd(a, b, x, y);
        
        printf("%d %d\n", x, y);
    }
    
    return 0;
}

线性同余方程

题目链接

活动 - AcWing 系统讲解常用算法与数据结构，给出相应代码模板，并会布置、讲解相应的基础算法题目。https://www.acwing.com/problem/content/880/

题解

可以转化为ax + my = b的形式，然后使用扩展欧几里得算法求解。

代码

#include <iostream>

using namespace std;

typedef long long LL;

int exgcd(int a, int b, int &x, int &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    
    int d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

int main()
{
    int n;
    scanf("%d", &n);
    
    while (n--)
    {
        int a, b, m;
        scanf("%d%d%d", &a, &b, &m);
        int x, y;
        int d = exgcd(a, m, x, y);
        if (b % d) puts("impossible");
        else printf("%d\n", (LL)x * (b / d) % m);
    }
    
    return 0;
}