图的表示
邻接矩阵和邻接表
稀疏图一般用邻接表表示(稀疏图:边数|E|远小于的图 )
稠密图更倾向于用邻接矩阵表示 (稠密图:边数|E|接近的图)
邻接矩阵可用于需要快速判断任意两个结点之间是否有边相连的应用场景。
如果用邻接表表示,为判断一条边(u,v)是否是图中的边,需要在邻接链表Adj[u]中搜索,效率较低。
图的检索和周游
被检测:在图中,当某结点的所有邻接结点都被访问了时, 称该结点被检测了。
经典的图检索算法:
-
宽度优先搜索(BFS)
- 从结点v开始,首先访问结点v,给v标上已访问标记。
- 访问邻接于v且目前尚未被访问的所有结点,此时结点v被 检测,而v的这些邻接结点是新的未被检测的结点。将这些结点依次放置到一个称为未检测结点表的队列中。
- 若未检测结点表为空,则算法终止;
- 否则,取未检测结点表的表头结点作为下一个待检测结点,重复上述过程。直到Q为空,算法终止。
设t(n,e)和s(n,e)是算法BFS在任一具有n个结点和 e 条边的图G上所花的时间和附加空间。 若G由邻接表表示,则 t(n,e)=Θ(n+e) 和 s(n,e)=Θ(n)。
若G由邻接矩阵表示,则 t(n,e)=Θ() 和 s(n,e)=Θ(n)
-
深度优先检索(DFS)

① DFS可以访问由v可到达的所有结点
② 如果t(n,e)和s(n,e)表示DFS对一n结点e条边的图所花的时间和附加空间,则
s(n,e)=Θ(n)
t(n,e)= Θ(n+e) G采用邻接表表示
t(n,e)= Θ() G采用邻接矩阵表示
图周游算法的应用
判定图G的连通性:若调用BFS的次数多于1次,则G 为非连通的。
生成图G的连通分图:一次调用BFS中所访问到的所 有结点及连接这些结点的边构成一个连通分图。
宽度优先生成树
向前边:BFS中由 u 到达未访问结点w的边(u,w)。
宽度优先生成树: 记T是BFS中处理的所有向前边集合。 若G是连通图,则BFS终止时,T构成一棵生成树,称为图G的宽度优先生成树。
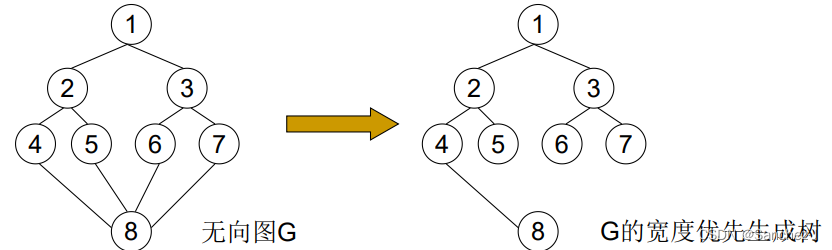
修改算法BFS:

深度优先周游算法DFT
反复调用DFS,直到所有结点均被检测到。
应用:
① 判定图G的连通性
② 连通分图
③ 无向图的自反传递闭包矩阵
④ 深度优先生成
D_Search深度检索
改造BFS算法,用栈来保存未被检测的结点,则得到的新的检索算法
注:结点被压入栈中后将以相反的次序出栈。
回溯法
用于求解问题的一组特定性质的解或满足某些约束条件的最优解。
什么样的问题适合用回溯法求解呢?
1)问题的解可用一个n元组(x1 ,…,xn )的向量来表示; 其中的xi取自于某个有穷集Si。
2)问题的求解目标是求取一个使某一规范函数P(x1 ,…,xn ) 取极值或满足该规范函数条件的向量(也可能是满足P的所有向量)。
约束条件:问题的解需要满足的条件,可以分为显式约束条件和隐式约束条件:
显式约束条件:一般用来规定每个xi的取值范围。 如 : xi≥0 即Si={所有非负实数} xi=0或xi=1 即 Si={0,1}
隐式约束条件:用来规定解空间中那些满足规范函数的元组, u 隐式约束条件描述了xi之间的关系和应满足的条件。
解空间:实例I的满足显式约束条件的所有元组,构成的解空间,即所有xi合法取值的元组的集合——可行解。
举例——8-皇后问题
在一个8×8棋盘上放置8个皇后,使得任意两个皇后之间 都不互相“攻击” ,即每两个皇后都不在同一行、同一列或同 一条斜角线上。
行、列号:1…8 皇后编号:1…8, 不失一般性,约定皇后i放到第i行的某一列上。
解的表示:用8-元组(x1 ,…,x8 )表示 ,其中xi是皇后i所在的列号。
显式约束条件:Si={1,2,3,4,5,6,7,8}, 1≤i≤8
解空间:所有可能的8元组,共有8^8个。
隐式约束条件:用来描述xi之间的关系,即没有两个xi可以相同,且没有两个皇后可以在同一条斜角线上。 由隐式约束条件可知:可能的解只能是( 1,2,3,4,5,6,7,8 )的 置换(排列),最多有8!个。
举例——子集和数问题
已知n个正数的集合W={w1 , w2 , …, wn}和正数M,找出W 中的和数等于M的所有子集。
子集和数问题解的表示
形式一:
问题的解为k-元组(x1 , x2 , …, xk), 1≤k≤n。不同的解可以是大小不同的元组,如(1,2,4)和(3,4)。
显式约束条件:xi∈{ j | j为整数且1≤j≤n }。
隐式约束条件:1)没有两个xi是相同的; 2)Wxi的和为M; 3)xi<xi+1 , 1≤ i<n(避免重复元组)
形式二 :
解由n-元组(x1 , x2 , …, xn )表示,其中xi∈{0,1}。如果选择了 wi,则xi=1,否则xi=0。
特点:所有元组具有统一固定的大小。
显式约束条件:xi∈{0,1} ,1≤i≤n;
隐式约束条件:Σ(xi × wi) = M
解空间的组织
回溯法将通过系统地检索给定问题的解空间来求解,从而需要有效地组织问题的解空间。
可以用树结构组织解空间,形成状态空间树。
如:4皇后问题的解空间树结构如图
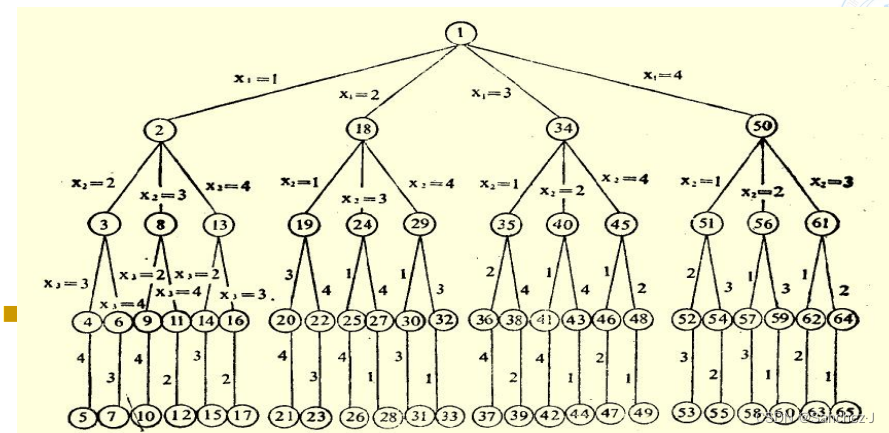
状态空间树:解空间的树结构称为状态空间树。
问题状态:树中的每一个结点代表问题的一个状态,称为问题状态。
状态空间:由根结点到其他结点的所有路径确定了这个问题的状态空间。
解状态:是这样一些问题状态S,对于这些问题状态,由根到S的那条路径确定了这个问题解空间中的一个元组。
答案状态:是这样的一些解状态S,对于这些解状态而言,由根到 S的这条路径确定了问题的一个解(满足隐式约束条件 的解)。
状态空间树的构造
以问题的初始状态作为根结点,然后系统地生成其它问题状态的结点。
在状态空间树生成的过程中,结点根据被检测情况分为三 类:
- 活结点:自己已经生成,但其儿子结点还没有全部生成并且 有待生成的结点。(静态)
- E-结点(expansion node):当前正在生成其儿子结点的 活结点。(动态)
- 死结点:不需要再进一步扩展或者其儿子结点已全部生成的结点。
构造状态空间树的两种策略
1. 深度优先策略:当E-结点R一旦生成一个新的儿子C时, C就变成一个新的E-结点,当完全检测了子树C之后,R结点再次成为E-结点。
2. 宽度优先策略:一个E-结点一直保持到变成死结点为止。
限界函数
在结点生成的过程中,定义一个限界函数,用来杀死还没有生成全部儿子结点的一些活结点 ——这些活结点已无法满足限界函数的条件, 因此不可能导致问题的答案。
回溯法:使用限界函数的深度优先状态结点生成方法称为回溯法(backtracking)
分支-限界方法:使用限界函数的 E 结点一直保持到死为止的状态结点生成方法称为分支-限界方法 (branch-and-bound)。
4皇后问题的回溯法求解
- 限界函数:如果(x1 ,x2 ,…,xi-1)是到当前E结点的路径, 那么xi-1的儿子结点xi是一些这样的结点, 它们使得(x1 ,x2 ,…,xi-1 ,xi)表示没有两个皇 后处在相互攻击状态的一种棋盘格局。
- 开始状态:根结点1,此时表示棋盘为空,还没有放置 任何皇后。
- 结点的生成:依次考察皇后1——皇后n的位置。
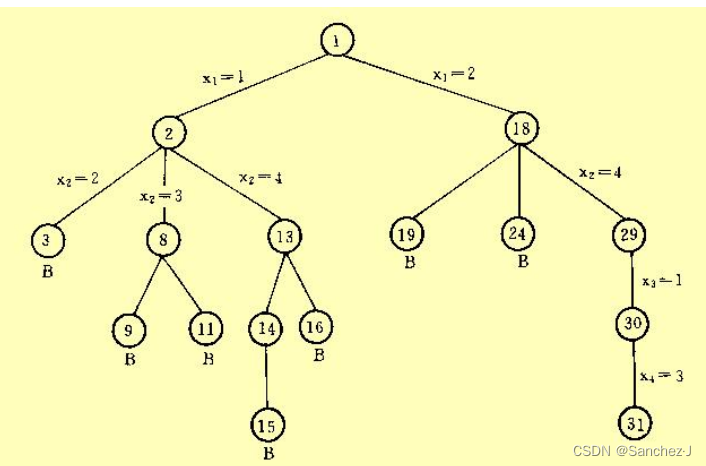
回溯法框架