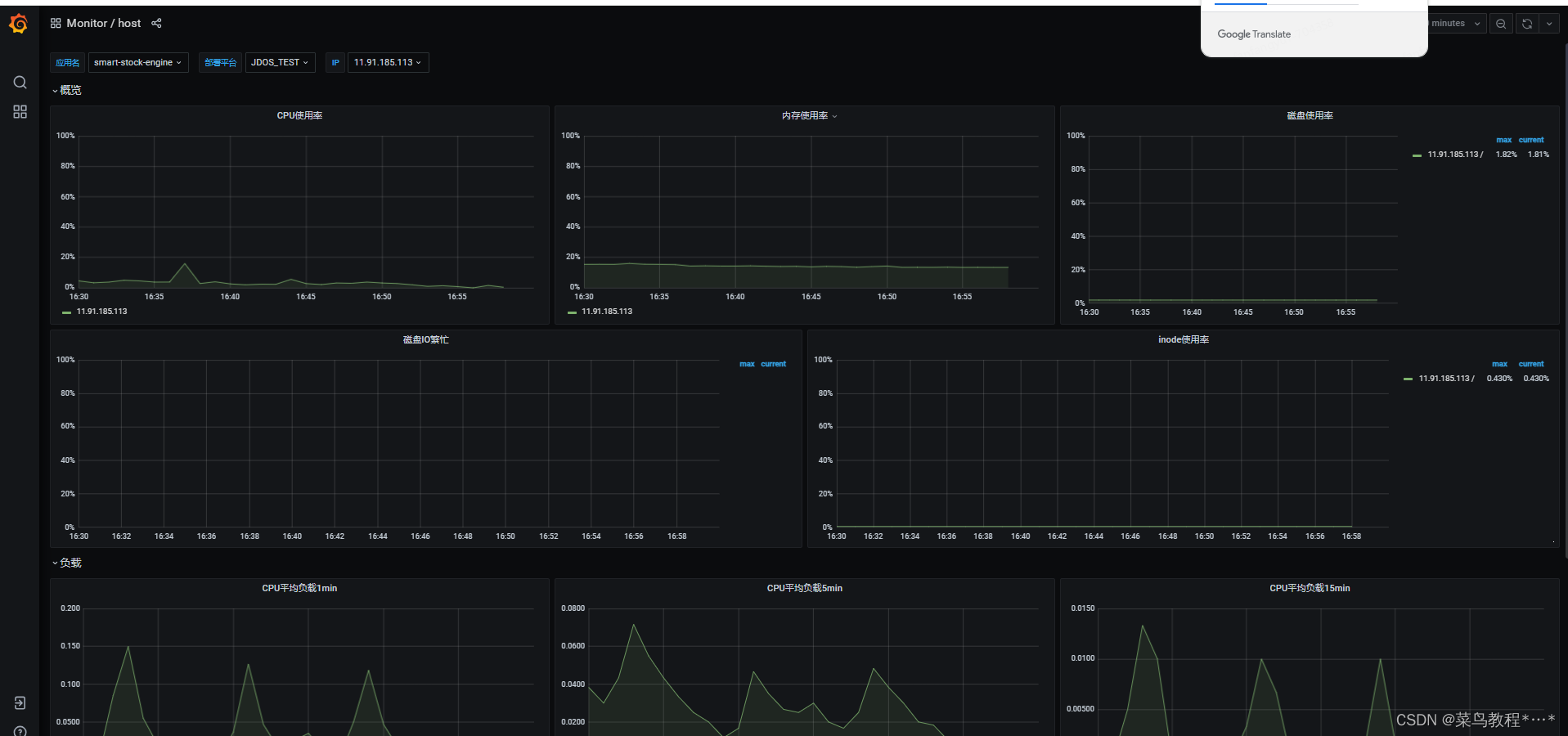
Jacobian matrix 雅可比矩阵

在后面的前向反向积累会用到。AD需要用到中间变量的导数，所以Jacobian matrix就是来计算这些的。

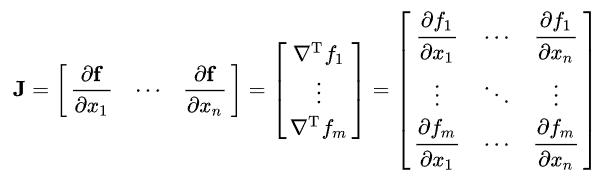
Hessian矩阵

在牛顿法的优化中有应用。

牛顿法 Newton-type methods

自动求导 Automatic Differentiation, AD

数值微分

import numpy as np

# 定义目标函数
def target_function(x):
    return x**2

# 数值方法计算一阶导数
def numerical_derivative_first_order(f, x, h=1e-5):
    return (f(x + h) - f(x - h)) / (2 * h)

# 数值方法计算二阶导数
def numerical_derivative_second_order(f, x, h=1e-5):
    return (f(x + h) - 2 * f(x) + f(x - h)) / (h * h)

# 在 x = 1 处计算函数值、一阶导数和二阶导数
x = 1.0
y = target_function(x)
dy_dx = numerical_derivative_first_order(target_function, x)
d2y_dx2 = numerical_derivative_second_order(target_function, x)

# 打印结果
print("Function value at x = 1:", y)
print("First derivative at x = 1:", dy_dx)
print("Second derivative at x = 1:", d2y_dx2)

可以用导数的定义计算，但是有误差。

符号微分

SymPy

博客 SymPy 符号计算基本教程
SymPy可以像人一样对符号求导，太强了。
貌似用了很多的匹配规则，不晓得怎么实现的，有点吊的。

符号微分的问题

即便SymPy这样的库已经可以对符号进行微分，但是一个函数的高次导会很复杂，表达式中会包含很多的重复计算，而这些重复的部分是可以简化的。如下图所示：

为了实现交替进行微分和简化的操作，AD应运而生。

自动微分

链式法则 Chain rule

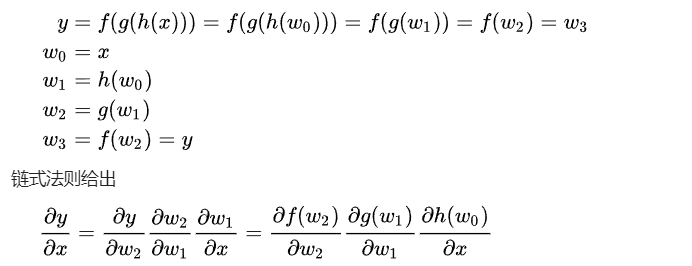
前向积累 forward accumulation

前向积累是比较直观的：


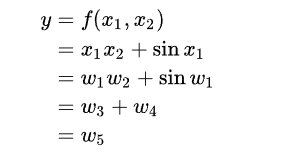
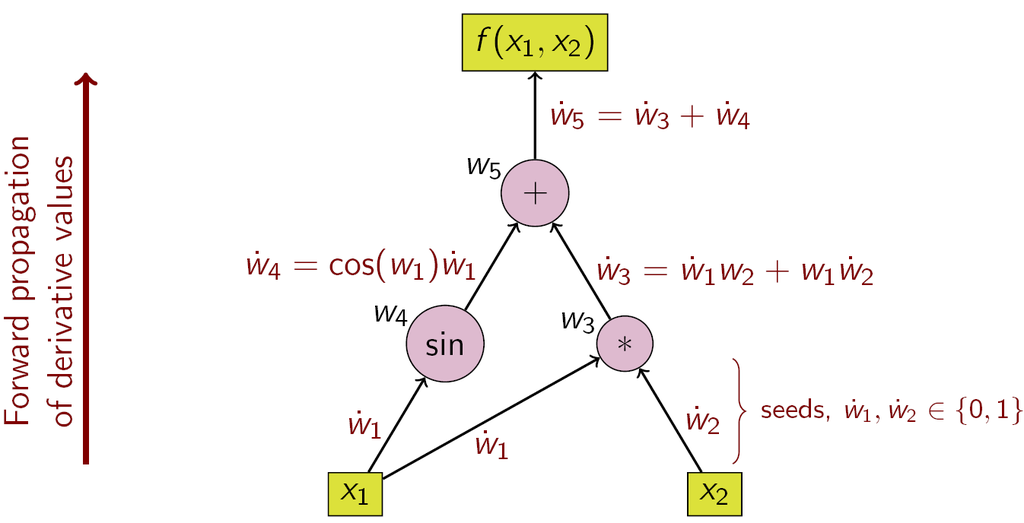
上面的seed就是用来求偏导的，求x1的偏导，seed={1，0}，x2就是seed={0,1}

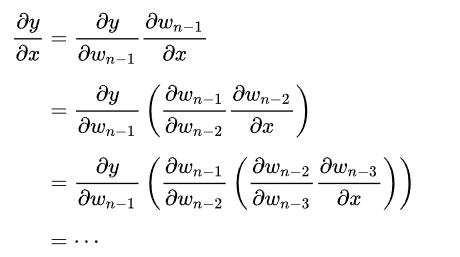
符合常规的求导过程。

反向积累 reverse accumulation

神经网络里的反向传播BP是反向积累的一个特例。

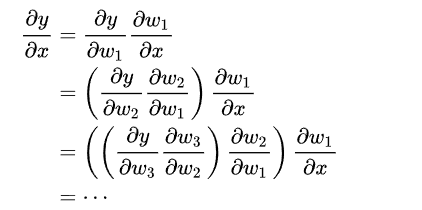
反向积累只需要令最后的f的seed={1}即可。理解起来不如前向积累直观，但是编程实现起来却更简洁速度也更快。

关键区别：
前向模式 AD： 需要对每个变量计算一次梯度，因此计算成本与变量数目成正比。适用于输入变量较少而输出变量较多的情况。
反向模式 AD： 仅需要对一个输出节点计算一次梯度，因此计算成本与输出节点数目成正比。适用于输入变量较多而输出变量较少的情况。——gpt

我觉得gpt说的有道理。

Automatic differentiation using dual numbers

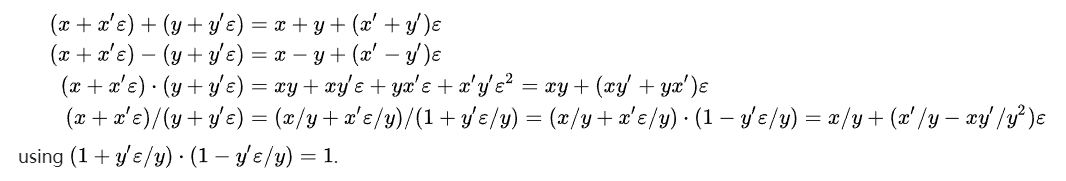
太吊了，把$x$ 用 $x+x^{{}^{\prime }}ϵ$表示，居然就可以计算导数了，太吊了！

class Dual:
    def __init__(self, realPart, infinitesimalPart=0):
        self.realPart = realPart
        self.infinitesimalPart = infinitesimalPart

    def __add__(self, other):
        return Dual(
            self.realPart + other.realPart,
            self.infinitesimalPart + other.infinitesimalPart
        )

    def __sub__(self, other):
        return Dual(
            self.realPart - other.realPart,
            self.infinitesimalPart - other.infinitesimalPart
        )

    def __mul__(self, other):
        return Dual(
            self.realPart * other.realPart,
            other.realPart * self.infinitesimalPart + self.realPart * other.infinitesimalPart
        )

    def __truediv__(self, other):
        realPart = self.realPart / other.realPart
        infinitesimalPart = (other.realPart * self.infinitesimalPart - self.realPart * other.infinitesimalPart) / (other.realPart ** 2)
        return Dual(realPart, infinitesimalPart)

# Example: Finding the partials of z = x * (x + y) + y * y at (x, y) = (2, 3)
def f(x, y):
    return y/x -x +y
    # return x * (x + y) + y * y
x = Dual(2)
y = Dual(3)
epsilon = Dual(0, 1)
a = f(x + epsilon, y)
b = f(x, y + epsilon)
print("∂z/∂x =", a.infinitesimalPart)  # Output: ∂z/∂x = 28
print("∂z/∂y =", b.infinitesimalPart)  # Output: ∂z/∂y = 81

这里的Dual类实现了加减乘除的求导，其余sin cos In exp的运算也类似。

当然这里的求导都是一次导，当导数变高阶的时候，可能会有所变化。

具体可能需要参考tensorflow和pytorch的源码
留个坑在这。

tensorflow和pytorch中的AD

源代码我没有看，框架比较复杂。
不过找到一个简易版的tinynn，对于学习应该是够用了。github
关于AD的部分就是ops.py文件，贴在下面：

"""Tensor operations (with autograd context)"""

import numpy as np


def as_tensor(obj):
    # avoid looping import
    from core.tensor import as_tensor
    return as_tensor(obj)


def build_binary_ops_tensor(ts1, ts2, grad_fn_ts1, grad_fn_ts2, values):
    requires_grad = ts1.requires_grad or ts2.requires_grad
    dependency = []
    if ts1.requires_grad:
        dependency.append(dict(tensor=ts1, grad_fn=grad_fn_ts1))
    if ts2.requires_grad:
        dependency.append(dict(tensor=ts2, grad_fn=grad_fn_ts2))
    tensor_cls = ts1.__class__
    return tensor_cls(values, requires_grad, dependency)


def build_unary_ops_tensor(ts, grad_fn, values):
    requires_grad = ts.requires_grad
    dependency = []
    if ts.requires_grad:
        dependency.append(dict(tensor=ts, grad_fn=grad_fn))
    tensor_cls = ts.__class__
    return tensor_cls(values, requires_grad, dependency)


def add_(ts1, ts2):
    values = ts1.values + ts2.values

    # c = a + b
    # D_c / D_a = 1.0
    # D_c / D_b = 1.0
    # also need to handle broadcasting
    def grad_fn_ts1(grad):
        # handle broadcasting (5, 3) + (3,) -> (5, 3)
        for _ in range(grad.ndim - ts1.values.ndim):
            grad = grad.sum(axis=0)
        # handle broadcasting (5, 3) + (1, 3) -> (5, 3)
        for i, dim in enumerate(ts1.shape):
            if dim == 1:
                grad = grad.sum(axis=i, keepdims=True)
        return grad

    def grad_fn_ts2(grad):
        for _ in range(grad.ndim - ts2.values.ndim):
            grad = grad.sum(axis=0)
        for i, dim in enumerate(ts2.shape):
            if dim == 1:
                grad = grad.sum(axis=i, keepdims=True)
        return grad

    return build_binary_ops_tensor(
        ts1, ts2, grad_fn_ts1, grad_fn_ts2, values)


def sub_(ts1, ts2):
    return ts1 + (-ts2)


def mul_(ts1, ts2):
    values = ts1.values * ts2.values

    # c = a * b
    # D_c / D_a = b
    # D_c / D_b = a
    def grad_fn_ts1(grad):
        grad = grad * ts2.values
        for _ in range(grad.ndim - ts1.values.ndim):
            grad = grad.sum(axis=0)
        for i, dim in enumerate(ts1.shape):
            if dim == 1:
                grad = grad.sum(axis=i, keepdims=True)
        return grad

    def grad_fn_ts2(grad):
        grad = grad * ts1.values
        for _ in range(grad.ndim - ts2.values.ndim):
            grad = grad.sum(axis=0)
        for i, dim in enumerate(ts2.shape):
            if dim == 1:
                grad = grad.sum(axis=i, keepdims=True)
        return grad

    return build_binary_ops_tensor(
        ts1, ts2, grad_fn_ts1, grad_fn_ts2, values)


def div_(ts1, ts2):
    values = ts1.values / ts2.values

    # c = a / b
    # D_c / D_a = 1 / b
    # D_c / D_b = -a / b**2
    def grad_fn_ts1(grad):
        grad = grad / ts2.values
        for _ in range(grad.ndim - ts1.values.ndim):
            grad = grad.sum(axis=0)
        for i, dim in enumerate(ts1.shape):
            if dim == 1:
                grad = grad.sum(axis=i, keepdims=True)
        return grad

    def grad_fn_ts2(grad):
        grad = -grad * ts1.values / ts2.values ** 2
        for _ in range(grad.ndim - ts2.values.ndim):
            grad = grad.sum(axis=0)
        for i, dim in enumerate(ts2.shape):
            if dim == 1:
                grad = grad.sum(axis=i, keepdims=True)
        return grad

    return build_binary_ops_tensor(
        ts1, ts2, grad_fn_ts1, grad_fn_ts2, values)


def pow_(ts1, ts2):
    values = ts1.values ** ts2.values

    # c = a ** b
    # D_c / D_a = b * a ** (b-1)
    # D_c / D_b = ln(a) * a ** b
    def grad_fn_ts1(grad):
        grad = grad * ts2.values * ts1.values ** (ts2.values - 1)
        for _ in range(grad.ndim - ts1.values.ndim):
            grad = grad.sum(axis=0)

        for i, dim in enumerate(ts1.shape):
            if dim == 1:
                grad = grad.sum(axis=i, keepdims=True)
        return grad

    def grad_fn_ts2(grad):
        grad = grad * (np.log(ts1.values) * values)
        for _ in range(grad.ndim - ts2.values.ndim):
            grad = grad.sum(axis=0)
        for i, dim in enumerate(ts2.shape):
            if dim == 1:
                grad = grad.sum(axis=i, keepdims=True)
        return grad

    return build_binary_ops_tensor(
        ts1, ts2, grad_fn_ts1, grad_fn_ts2, values)


def dot_(ts1, ts2):
    values = ts1.values @ ts2.values

    # c = a @ b
    # D_c / D_a = grad @ b.T
    # D_c / D_b = a.T @ grad
    def grad_fn_ts1(grad):
        return grad @ ts2.values.T

    def grad_fn_ts2(grad):
        return ts1.values.T @ grad

    return build_binary_ops_tensor(
        ts1, ts2, grad_fn_ts1, grad_fn_ts2, values)


def maximum_(ts1, ts2):
    values = np.maximum(ts1.values, ts2.values)

    def grad_fn_ts1(grad):
        grad = grad * (ts1.values >= ts2.values)
        for _ in range(grad.ndim - ts1.values.ndim):
            grad = grad.sum(axis=0)
        for i, dim in enumerate(ts1.shape):
            if dim == 1:
                grad = grad.sum(axis=i, keepdims=True)
        return grad

    def grad_fn_ts2(grad):
        grad = grad * (ts2.values > ts1.values)
        for _ in range(grad.ndim - ts2.values.ndim):
            grad = grad.sum(axis=0)
        for i, dim in enumerate(ts2.shape):
            if dim == 1:
                grad = grad.sum(axis=i, keepdims=True)
        return grad

    return build_binary_ops_tensor(
        ts1, ts2, grad_fn_ts1, grad_fn_ts2, values)


def minimum_(ts1, ts2):
    values = np.minimum(ts1.values, ts2.values)

    def grad_fn_ts1(grad):
        grad = grad * (ts1.values <= ts2.values)
        for _ in range(grad.ndim - ts1.values.ndim):
            grad = grad.sum(axis=0)
        for i, dim in enumerate(ts1.shape):
            if dim == 1:
                grad = grad.sum(axis=i, keepdims=True)
        return grad

    def grad_fn_ts2(grad):
        grad = grad * (ts2.values < ts1.values)
        for _ in range(grad.ndim - ts2.values.ndim):
            grad = grad.sum(axis=0)
        for i, dim in enumerate(ts2.shape):
            if dim == 1:
                grad = grad.sum(axis=i, keepdims=True)
        return grad

    return build_binary_ops_tensor(
        ts1, ts2, grad_fn_ts1, grad_fn_ts2, values)


def exp_(ts):
    values = np.exp(ts.values)

    def grad_fn(grad):
        return values * grad

    return build_unary_ops_tensor(ts, grad_fn, values)


def max_(ts, axis=None):
    values = np.max(ts.values, axis=axis)

    def grad_fn(grad):
        return grad * (ts.values.max(axis=axis, keepdims=1) == ts.values)

    return build_unary_ops_tensor(ts, grad_fn, values)


def min_(ts, axis=None):
    values = np.min(ts.values, axis=axis)

    def grad_fn(grad):
        return grad * (ts.values.min(axis=axis, keepdims=1) == ts.values)

    return build_unary_ops_tensor(ts, grad_fn, values)


def log_(ts):
    values = np.log(ts.values)

    def grad_fn(grad):
        return grad / ts.values

    return build_unary_ops_tensor(ts, grad_fn, values)


def sum_(ts, axis):
    values = ts.values.sum(axis=axis)
    if axis is not None:
        repeat = ts.values.shape[axis]

    def grad_fn(grad):
        if axis is None:
            grad = grad * np.ones_like(ts.values)
        else:
            grad = np.expand_dims(grad, axis)
            grad = np.repeat(grad, repeat, axis)
        return grad

    return build_unary_ops_tensor(ts, grad_fn, values)


def transpose_(ts, axes=None):
    values = ts.values.transpose(axes)

    if axes is None:
        axes = reversed(range(ts.values.ndim))
    axes = list(axes)

    # recover to original shape
    def grad_fn(grad):
        return grad.transpose(np.argsort(axes))

    return build_unary_ops_tensor(ts, grad_fn, values)


def getitem_(ts, key):
    values = ts.values[key]

    def grad_fn(grad):
        recover_grad = np.zeros_like(ts.values)
        recover_grad[key] = grad
        return recover_grad

    return build_unary_ops_tensor(ts, grad_fn, values)


def neg_(ts):
    values = -ts.values

    def grad_fn(grad):
        return -grad

    return build_unary_ops_tensor(ts, grad_fn, values)


def reshape_(ts, newshape):
    shape = ts.values.shape
    values = ts.values.reshape(newshape)

    def grad_fn(grad):
        return grad.reshape(shape)

    return build_unary_ops_tensor(ts, grad_fn, values)


def pad_(ts, pad_width, mode):
    values = np.pad(ts.values, pad_width=pad_width, mode=mode)
    slices = list()
    for size, (before, after) in zip(values.shape, pad_width):
        slices.append(slice(before, size-after))

    def grad_fn(grad):
        return grad[tuple(slices)]

    return build_unary_ops_tensor(ts, grad_fn, values)


def flatten_(ts):
    shape = ts.shape
    values = ts.values.ravel()

    def grad_fn(grad):
        return grad.reshape(shape)
    return build_unary_ops_tensor(ts, grad_fn, values)


def clip_(ts, min, max):
    values = ts.values.clip(min, max)

    mask = np.ones(ts.shape, dtype=bool)
    if min is not None:
        mask &= ts.values >= min
    if max is not None:
        mask &= ts.values <= max

    def grad_fn(grad):
        return grad * mask
    return build_unary_ops_tensor(ts, grad_fn, values)


def max(obj, axis=None):
    return max_(as_tensor(obj), axis=axis)


def maximum(obj1, obj2):
    return maximum_(as_tensor(obj1), as_tensor(obj2))


def minimum(obj1, obj2):
    return minimum_(as_tensor(obj1), as_tensor(obj2))


def exp(obj):
    return exp_(as_tensor(obj))


def sum(obj, axis=None):
    return sum_(as_tensor(obj), axis=axis)


def log(obj):
    return log_(as_tensor(obj))


def reshape(obj, newshape):
    return reshape_(as_tensor(obj), newshape)


def pad(obj, pad_width, mode="constant"):
    return pad_(as_tensor(obj), pad_width, mode=mode)


def flatten(obj):
    return flatten_(as_tensor(obj))


def clip(obj, min=None, max=None):
    return clip_(as_tensor(obj), min, max)

所以似乎这些深度学习框架似乎并没有按照交替进行符号求导和简化的步骤去进行AD。而是把每一个算子的梯度计算方法都写了出来。这样当我们去训练神经网络的时候，下，下，显存除了要存本来的参数，还要存梯度信息。这就会增大开销，所以为什么有
zero_grad 这样的操作。

class Tensor:
    # ...
    def zero_grad(self):
        self.grad = np.zeros(self.shape)

参考：PyTorch中在反向传播前为什么要手动将梯度清零？
一文详解pytorch的“动态图”与“自动微分”技术