前言
本专栏旨在通过分类学习算法,使您能够牢固掌握不同算法的理论要点。通过策略性地练习精选的经典题目,帮助您深度理解每种算法,避免出现刷了很多算法题,还是一知半解的状态
专栏导航
- 二分查找
- 回溯
- 双指针
- 滑动窗口
- 深度优先搜索
- 广度优先搜索
算法解析
回溯(Backtracking)是一种通过试错来解决问题的算法思想。当它通过尝试分步去解决一个问题时,如果发现现有的分步答案不能得到有效的正确的解答时,它将取消上一步甚至是上几步的计算,再通过其他的可能的分步解答再次尝试寻找问题的答案。
回溯法通常用递归方式来实现,在解决问题的过程中尝试各种可能的分步方法。如果某一步骤失败了,回溯算法会退回到上一步骤,然后尝试另一种方法。回溯法常用于解决如下问题:
- 组合问题:求解一个问题的所有满足条件的组合方式。
- 排列问题:求解一个问题的所有满足条件的排列方式。
- 划分问题:求解将一个对象分成几部分的方法。
- 子集构造问题:求解一个集合的所有子集。
- 棋盘问题:如八皇后问题、解数独和跳马问题等。
- 图的遍历问题:如哈密顿路径问题、图的着色问题等。
回溯算法的关键在于解决决策树的遍历过程中,如何剪枝。剪枝通过检测是否已经不可能得到正确的解来减少不必要的计算。在实现回溯算法时,通常有以下几个步骤:
- 选择:选择下一个可能的分步解答。
- 约束:检查到目前为止的解答序列是否满足约束条件(即是否“合法”)。
- 目标:检查到目前为止的解答序列是否满足解答条件(即是否已经找到一个解答)。
如果以上步骤中的任何一步不能继续下去,那么就执行回溯(返回上一步),尝试其他可能的路径。这种算法可以看作穷举搜索的一种优化,它利用问题的约束条件大大减少了搜索空间。
回溯算法和深度优先搜索(DFS)有密切的关系,实际上,回溯算法可以视为带有剪枝功能的深度优先搜索。在实现时,通常使用递归方法来模拟整个决策树的深度优先遍历过程,递归结构的本质上是栈结构,与DFS的实现方式一致。
实战练习
组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
提示:
1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素 互不相同
1 <= target <= 40
官方题解
全排列II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
1 <= nums.length <= 8
-10 <= nums[i] <= 10
官方题解
单词搜索
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例 1:
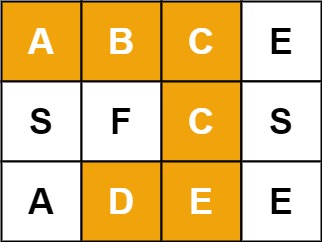
输入:board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
输出:true
示例 2:
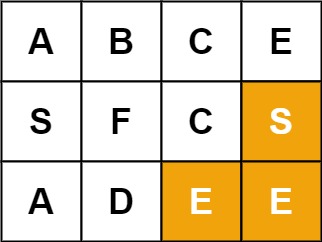
输入:board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “SEE”
输出:true
示例 3:

输入:board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCB”
输出:false
提示:
m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board 和 word 仅由大小写英文字母组成
进阶: 你可以使用搜索剪枝的技术来优化解决方案,使其在 board 更大的情况下可以更快解决问题?
官方题解