2023-12-26分割回文串和子集以及子集II

131. 分割回文串

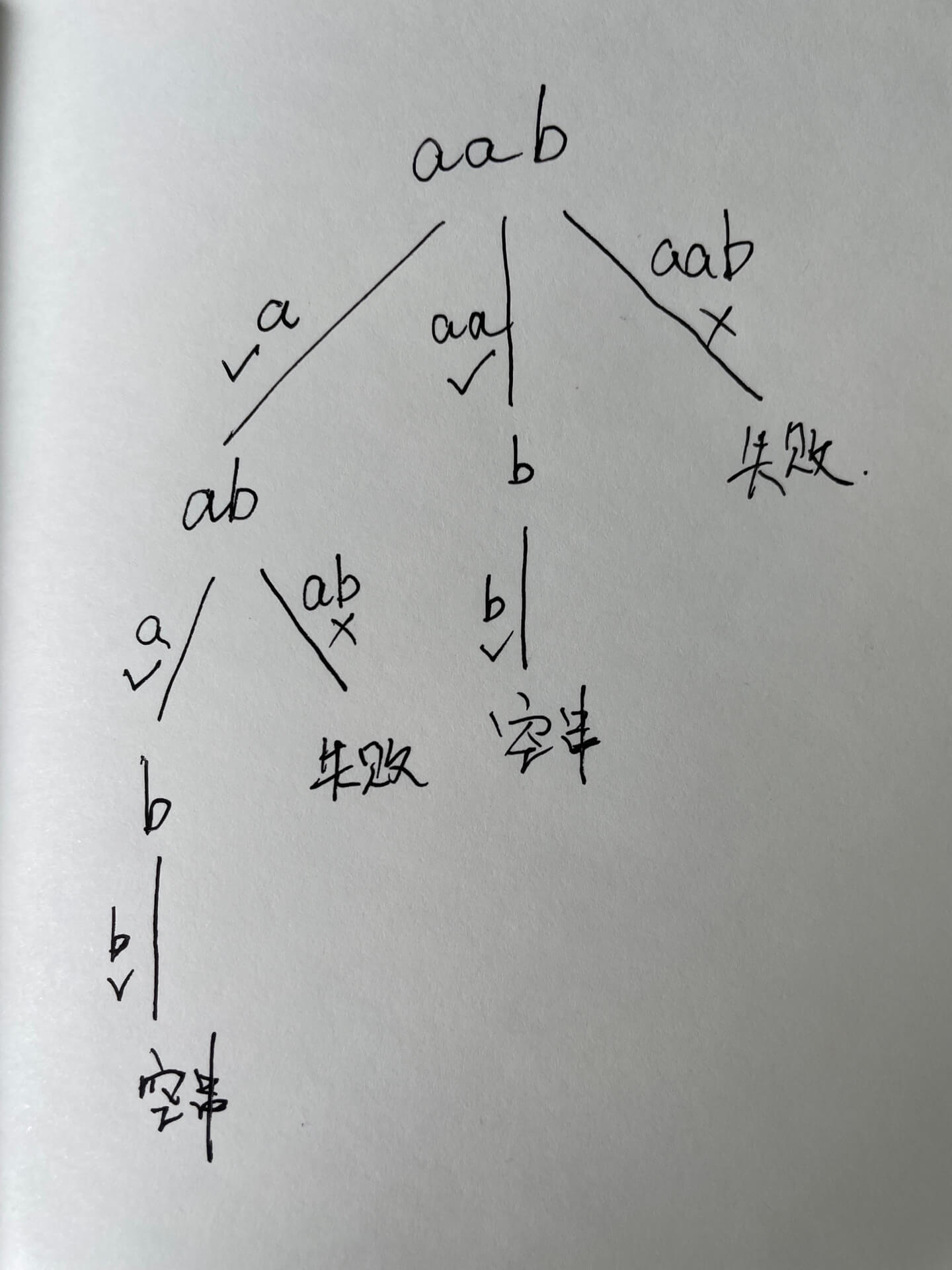
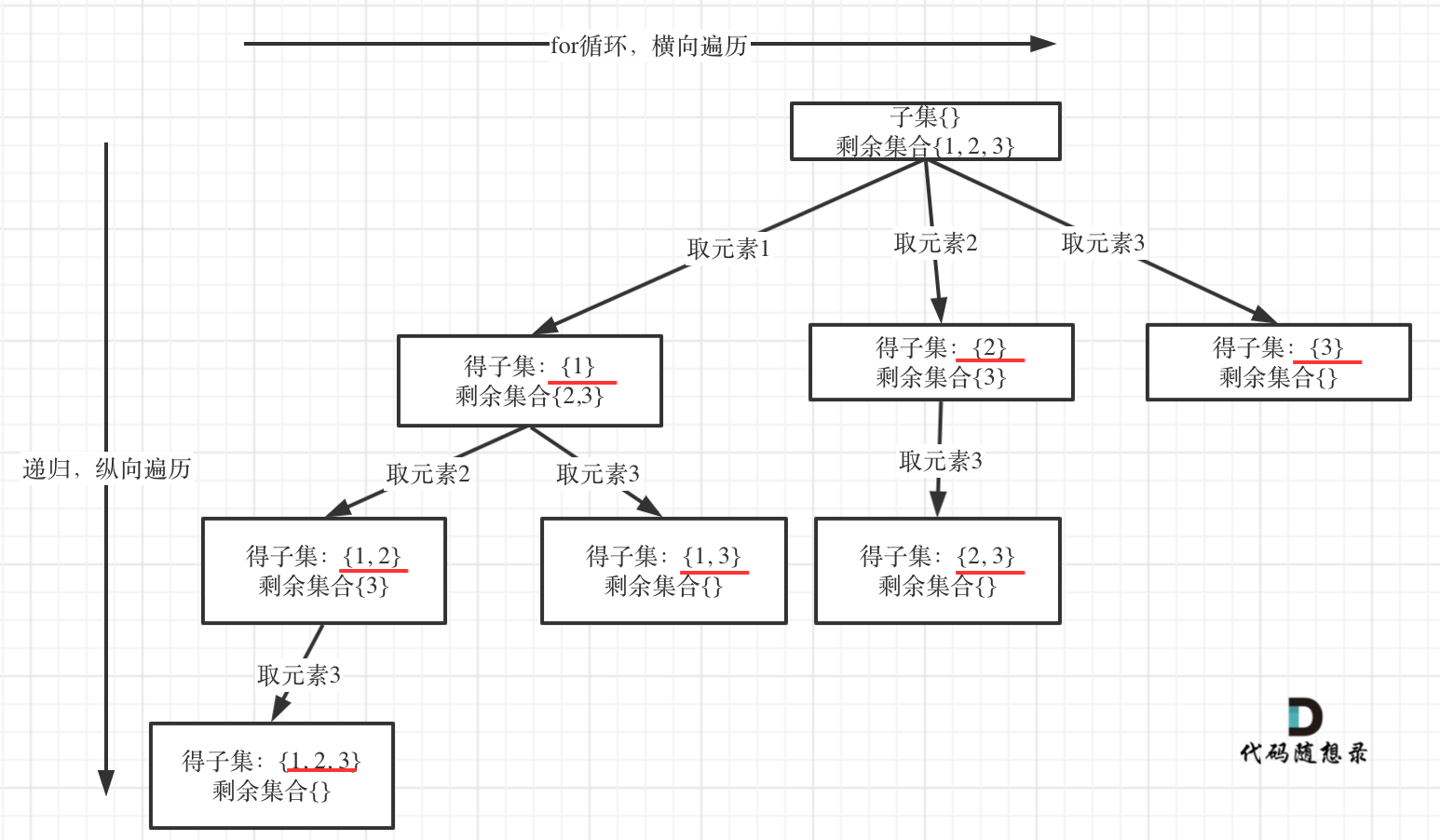
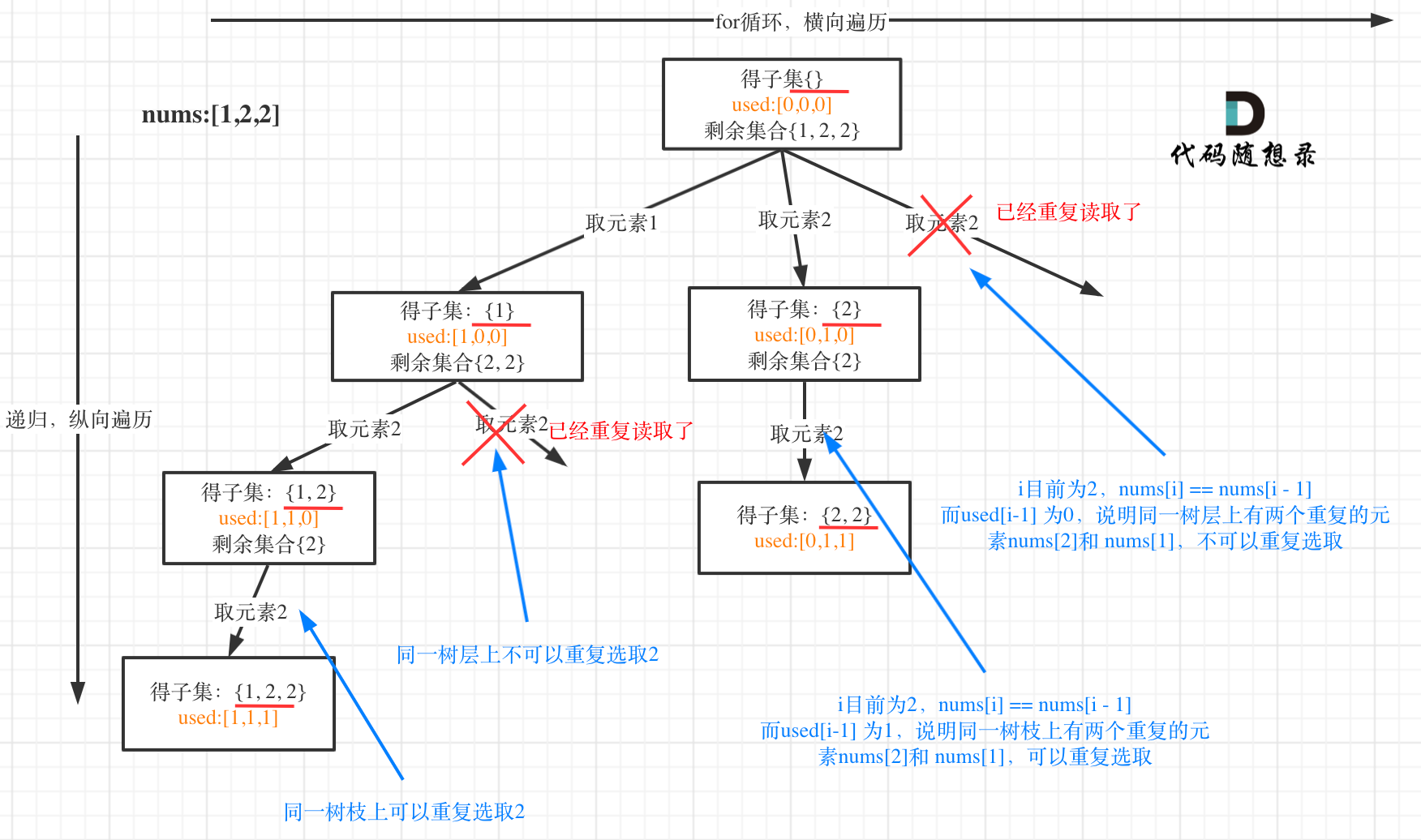
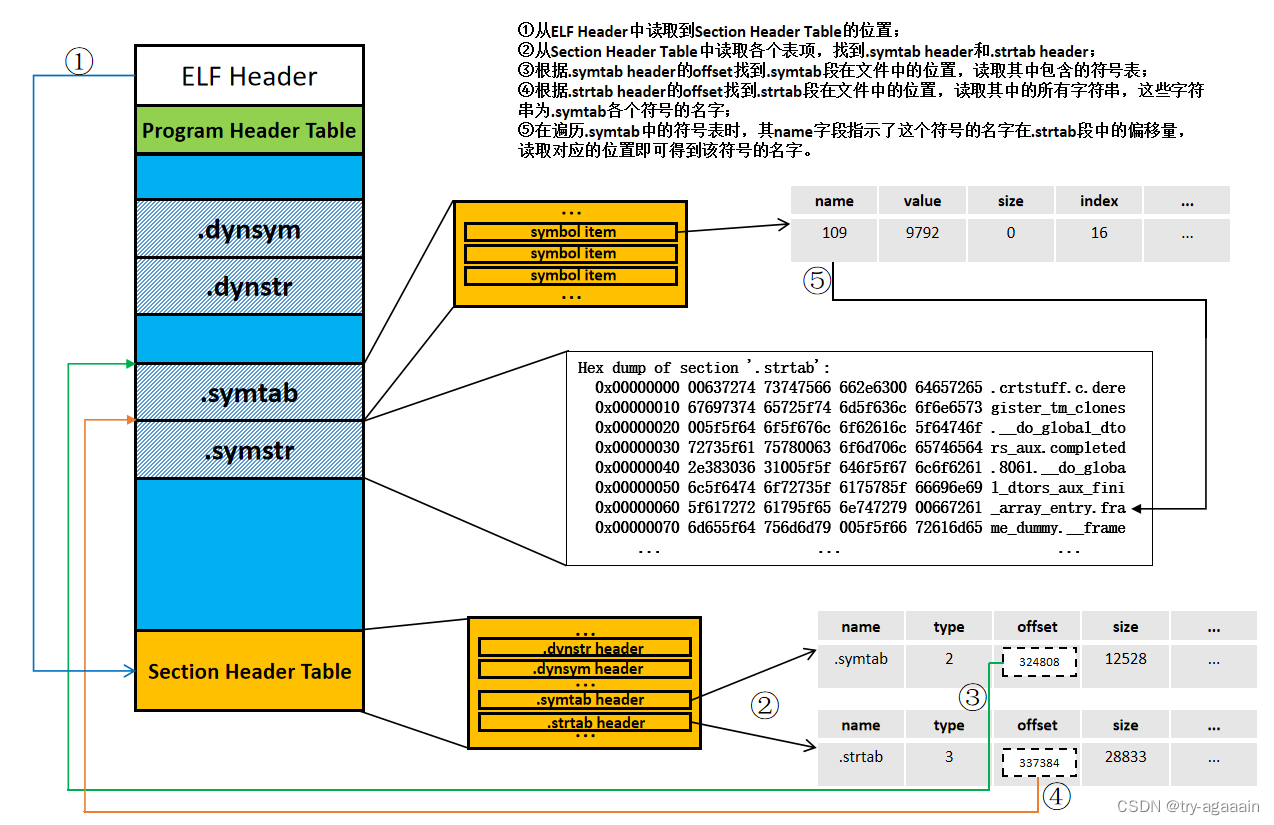
思想：回溯三步骤！① 传入参数 ② 回溯结束条件 ③ 单层搜索逻辑！抽象成回溯树，树枝上是每次从头部穷举切分出的子串，节点上是待切分的剩余字符串【从头开始每次往后加一】

class Solution:
    def partition(self, s: str) -> List[List[str]]:
        result = []
        self.backtrack(s,0,[],result)
        return result
    
    def backtrack(self, s, start, temp_list, result):
        # 结束条件？当start遍历到s的长度的时候说明子串都满足条件
        if start == len(s):
            # [:]这个很重要！不小心的会丢失了数据
            result.append(temp_list[:])
            return 
        for i in range(start,len(s)):
            # 如果满足子串是回文串继续递归，否则在原基础往后移动
            if self.huiwenchuan(s, start, i):
                # 当前节点 i + 1
                temp_list.append(s[start:i + 1])
                self.backtrack(s, i + 1, temp_list, result)
                # 回溯操作
                temp_list.pop()
    # 判断回文子串
    def huiwenchuan(self, s, start1, end1):
        start = start1
        end = end1
        while start < end:
            if s[start] != s[end]:
                return False
            start += 1
            end -= 1
        return True

78. 子集

思路：组合问题和分割问题就是收集回溯树叶子节点！而子集就是找树的所有节点！需要考虑是否有序？其实子集也是一种组合问题，因为它的集合是无序的，子集{1,2} 和子集{2,1}是一样的。那么既然是无序，取过的元素不会重复取，写回溯算法的时候，for就要从startIndex开始，而不是从0开始！

78.子集

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        result = []
        result.append([])
        self.backtrack(nums, [], 0, result)
        return result
        
    def backtrack(self, nums, temp_list, start_index, result):
        if len(temp_list) >= 1:
            result.append(temp_list[:])
            # 取树上的节点了 不需要return i + 1 会自动结束
        for i in range(start_index, len(nums)):
            temp_list.append(nums[i])
            self.backtrack(nums, temp_list, i + 1, result)
            temp_list.pop()

90. 子集 II

思路：和78.子集 (opens new window)区别就是集合里有重复元素了，而且求取的子集要去重。简单一点就排序后，进行获取子集！或者树层去重或树枝去重

class Solution:
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        result = []
        result.append([])
        nums.sort()   # 为什么加了这个就能通过？对子集进行排序的时候会发现有重复的子集了
        self.backtrack(nums, [], 0, result)
        return result
        
    def backtrack(self, nums, temp_list, start_index, result):
       # 关键是去重
        if len(temp_list) >= 1:
            if temp_list not in result:
                result.append(temp_list[:])
            # 取树上的节点了 不需要return
        for i in range(start_index, len(nums)):
            temp_list.append(nums[i])
            self.backtrack(nums, temp_list, i + 1, result)
            temp_list.pop()
            
class Solution:
    def subsetsWithDup(self, nums):
        result = []
        path = []
        nums.sort()  # 去重需要排序
        self.backtracking(nums, 0, path, result)
        return result

    def backtracking(self, nums, startIndex, path, result):
        result.append(path[:])  # 收集子集
        uset = set()
        for i in range(startIndex, len(nums)):
            if nums[i] in uset:
                continue
            uset.add(nums[i])
            path.append(nums[i])
            self.backtracking(nums, i + 1, path, result)
            path.pop()
class Solution:
    def subsetsWithDup(self, nums):
        result = []
        path = []
        used = [False] * len(nums)
        nums.sort()  # 去重需要排序
        self.backtracking(nums, 0, used, path, result)
        return result

    def backtracking(self, nums, startIndex, used, path, result):
        result.append(path[:])  # 收集子集
        for i in range(startIndex, len(nums)):
            # used[i - 1] == True，说明同一树枝 nums[i - 1] 使用过
            # used[i - 1] == False，说明同一树层 nums[i - 1] 使用过
            # 而我们要对同一树层使用过的元素进行跳过
            if i > 0 and nums[i] == nums[i - 1] and not used[i - 1]:
                continue
            path.append(nums[i])
            used[i] = True
            self.backtracking(nums, i + 1, used, path, result)
            used[i] = False
            path.pop()