目录
- 前言
- 基本求导规则
- 1. 向量变元的实值标量函数
- 1.1 4个法则
- 1.2 常用公式
- 2. 矩阵变元的实值标量函数
- 2.1 4个法则
- 2.2 常用公式
- 参考
前言
这篇笔记的内容是基于参考的文章写出的,公式部分可以会沿用文章本来的式,但会加入我自己的一些思考以及注释,如果读者认为我写的不够好得话可以参考原文章~
本笔记的内容是学习向量变元的实值标量函数、矩阵变元的实值标量函数中最基础的矩阵求导公式(会对个别重要的公式做证明)。
下面有一个求矩阵导数的网站,可以用来验证求导结果是否正确:Matrix Calculus
基本求导规则
1. 向量变元的实值标量函数
即形如 f ( x ⃗ ) , x ⃗ = [ x 1 , x 2 , ⋯ , x n ] T f(\vec{x}),\vec{x}=[x_1,x_2,\cdots,x_n]^T f(x),x=[x1,x2,⋯,xn]T使用梯度向量形式,则有 ∇ x ⃗ f ( x ⃗ ) = ∂ f ( x ⃗ ) ∂ x ⃗ = [ ∂ f ∂ x 1 , ∂ f ∂ x 2 , ⋯ , ∂ f ∂ x n ] T \nabla_{\vec{x}}f(\vec{x})=\frac{\partial f(\vec{x})}{\partial\vec{x}}=\left[\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\cdots,\frac{\partial f}{\partial x_n}\right]^T ∇xf(x)=∂x∂f(x)=[∂x1∂f,∂x2∂f,⋯,∂xn∂f]T对于该形式的求导法则,与高等数学中的导数的法则的证明思想类似,下面给个4个原则,并选择性给出证明:
1.1 4个法则
(1):常数求导
与一元函数常数求导相同:结果为零向量,即
∂ c ∂ x ⃗ = 0 n × 1 \frac{\partial c}{\partial\vec{x}}=\mathbf{0}_{n\times1} ∂x∂c=0n×1其中, c c c 为常数
(2):线性法则
与一元函数求导线性法则相同:相加再求导等于求导再相加,常数提到外面,即: ∂ [ c 1 f ( x ⃗ ) + c 2 g ( x ⃗ ) ] ∂ x ⃗ = c 1 ∂ f ( x ⃗ ) ∂ x ⃗ + c 2 ∂ g ( x ⃗ ) ∂ x ⃗ \frac{\partial[c_1f(\vec{x})+c_2g(\vec{x})]}{\partial\vec{x}}=c_1\frac{\partial f(\vec{x})}{\partial\vec{x}}+c_2\frac{\partial g(\vec{x})}{\partial\vec{x}} ∂x∂[c1f(x)+c2g(x)]=c1∂x∂f(x)+c2∂x∂g(x)其中, c 1 , c 2 c_1,c_2 c1,c2 为常数。
(3):乘积法则
与一元函数求导乘积法则相同:前导后不导加前不导后导,即
∂ [ f ( x ⃗ ) g ( x ⃗ ) ] ∂ x ⃗ = ∂ f ( x ⃗ ) ∂ x ⃗ g ( x ⃗ ) + f ( x ⃗ ) ∂ g ( x ⃗ ) ∂ x ⃗ \frac{\partial[f(\vec{x})g(\vec{x})]}{\partial\vec{x}}=\frac{\partial f(\vec{x})}{\partial\vec{x}}g(\vec{x})+f(\vec{x})\frac{\partial g(\vec{x})}{\partial\vec{x}} ∂x∂[f(x)g(x)]=∂x∂f(x)g(x)+f(x)∂x∂g(x)证明: ∂ [ f ( x ⃗ ) g ( x ⃗ ) ] ∂ x ⃗ = [ ∂ ( f g ) ∂ x 1 ∂ ( f g ) ∂ x 2 ⋮ ∂ ( f g ) ∂ x n ] = [ ∂ f ∂ x 1 g + f ∂ g ∂ x 1 ∂ f ∂ x 2 g + f ∂ g ∂ x 2 ⋮ ∂ f ∂ x n g + f ∂ g ∂ x n ] = [ ∂ f ∂ x 1 ∂ f ∂ x 2 ⋮ ∂ f ∂ x n ] g + f [ ∂ g ∂ x 1 ∂ g ∂ x 2 ⋮ ∂ g ∂ x n ] = ∂ f ( x ⃗ ) ∂ x ⃗ g ( x ⃗ ) + f ( x ⃗ ) ∂ g ( x ⃗ ) ∂ x ⃗ \begin{aligned} \frac{\partial[f(\vec{x})g(\vec{x})]}{\partial \vec{x}}& =\begin{bmatrix}\frac{\partial(fg)}{\partial x_1}\\\frac{\partial(fg)}{\partial x_2}\\\vdots\\\frac{\partial(fg)}{\partial x_n}\end{bmatrix} \\ &=\begin{bmatrix}\frac{\partial f}{\partial x_1}g+f\frac{\partial g}{\partial x_1}\\\frac{\partial f}{\partial x_2}g+f\frac{\partial g}{\partial x_2}\\\vdots\\\frac{\partial f}{\partial x_n}g+f\frac{\partial g}{\partial x_n}\end{bmatrix} \\ &\left.=\left[\begin{array}{c}\frac{\partial f}{\partial x_1}\\\frac{\partial f}{\partial x_2}\\\vdots\\\frac{\partial f}{\partial x_n}\end{array}\right.\right]g+f\left[\begin{array}{c}\frac{\partial g}{\partial x_1}\\\frac{\partial g}{\partial x_2}\\\vdots\\\frac{\partial g}{\partial x_n}\end{array}\right] \\ &=\frac{\partial f(\vec{x})}{\partial\vec{x}}g(\vec{x})+f(\vec{x})\frac{\partial g(\vec{x})}{\partial\vec{x}} \end{aligned} ∂x∂[f(x)g(x)]= ∂x1∂(fg)∂x2∂(fg)⋮∂xn∂(fg) = ∂x1∂fg+f∂x1∂g∂x2∂fg+f∂x2∂g⋮∂xn∂fg+f∂xn∂g = ∂x1∂f∂x2∂f⋮∂xn∂f g+f ∂x1∂g∂x2∂g⋮∂xn∂g =∂x∂f(x)g(x)+f(x)∂x∂g(x)
(4):商法则
与一元函数求导商法则相同:(上导下不导 减 上不导下导)除以(下的平方): ∂ [ f ( x ⃗ ) g ( x ⃗ ) ] ∂ x ⃗ = 1 g 2 ( x ⃗ ) [ ∂ f ( x ⃗ ) ∂ x ⃗ g ( x ⃗ ) − f ( x ⃗ ) ∂ g ( x ⃗ ) ∂ x ⃗ ] \begin{aligned}&\frac{\partial\left[\frac{f(\vec{x})}{g(\vec{x})}\right]}{\partial\vec{x}}=\frac1{g^2(\vec{x})}\left[\frac{\partial f(\vec{x})}{\partial\vec{x}}g(\vec{x})-f(\vec{x})\frac{\partial g(\vec{x})}{\partial\vec{x}}\right]\\\end{aligned} ∂x∂[g(x)f(x)]=g2(x)1[∂x∂f(x)g(x)−f(x)∂x∂g(x)]其中, g ( x ⃗ ) ≠ 0 g(\vec{x})\neq0 g(x)=0
证明: ∂ [ f ( x ⃗ ) g ( x ⃗ ) ] ∂ x ⃗ = [ ∂ ( f g ) ∂ x 1 ∂ ( f g ) ∂ x 2 ⋮ ∂ ( f g ) ∂ x n ] = [ 1 g 2 ( ∂ f ∂ x 1 g − f ∂ g ∂ x 1 ) 1 g 2 ( ∂ f ∂ x 2 g − f ∂ g ∂ x 2 ) ⋮ 1 g 2 ( ∂ f ∂ x n g − f ∂ g ∂ x n ) ] = 1 g 2 ( [ ∂ f ∂ x 1 ∂ f ∂ x 2 ⋮ ∂ f ∂ x n ] g − f [ ∂ g ∂ x 1 ∂ g ∂ x 2 ⋮ ∂ g ∂ x n ] ) = 1 g 2 ( x ⃗ ) [ ∂ f ( x ⃗ ) ∂ x ⃗ g ( x ⃗ ) − f ( x ⃗ ) ∂ g ( x ⃗ ) ∂ x ⃗ ] \begin{aligned} \frac{\partial\left[\frac{f(\vec{x})}{g(\vec{x})}\right]}{\partial\vec{x}}& \left.=\left[\begin{array}{c}\dfrac{\partial(\frac{f}{g})}{\partial x_1}\\\dfrac{\partial(\frac{f}{g})}{\partial x_2}\\\vdots\\\dfrac{\partial(\frac{f}{g})}{\partial x_n}\end{array}\right.\right] \\ &=\begin{bmatrix}\frac{1}{g^2}\left(\frac{\partial f}{\partial x_1}g-f\frac{\partial g}{\partial x_1}\right)\\\frac{1}{g^2}\left(\frac{\partial f}{\partial x_2}g-f\frac{\partial g}{\partial x_2}\right)\\\vdots\\\frac{1}{g^2}\left(\frac{\partial f}{\partial x_n}g-f\frac{\partial g}{\partial x_n}\right)\end{bmatrix} \\ &\left.\left.=\frac{1}{g^2}\left(\left[\begin{array}{c}\frac{\partial f}{\partial x_1}\\\frac{\partial f}{\partial x_2}\\\vdots\\\frac{\partial f}{\partial x_n}\end{array}\right.\right.\right]g-f\left[\begin{array}{c}\frac{\partial g}{\partial x_1}\\\frac{\partial g}{\partial x_2}\\\vdots\\\frac{\partial g}{\partial x_n}\end{array}\right]\right) \\ &=\frac{1}{g^{2}(\vec{x})}\left[\frac{\partial f(\vec{x})}{\partial\vec{x}}g(\vec{x})-f(\vec{x})\frac{\partial g(\vec{x})}{\partial\vec{x}}\right] \end{aligned} ∂x∂[g(x)f(x)]= ∂x1∂(gf)∂x2∂(gf)⋮∂xn∂(gf) = g21(∂x1∂fg−f∂x1∂g)g21(∂x2∂fg−f∂x2∂g)⋮g21(∂xn∂fg−f∂xn∂g) =g21 ∂x1∂f∂x2∂f⋮∂xn∂f g−f ∂x1∂g∂x2∂g⋮∂xn∂g =g2(x)1[∂x∂f(x)g(x)−f(x)∂x∂g(x)]如上所述,证明完毕
1.2 常用公式
(1):
∂
(
x
⃗
T
a
⃗
)
∂
x
⃗
=
∂
(
a
⃗
T
x
⃗
)
∂
x
⃗
=
a
⃗
\frac{\partial(\vec{x}^T\vec{a})}{\partial\vec{x}}=\frac{\partial(\vec{a}^T\vec{x})}{\partial\vec{x}}=\vec{a}
∂x∂(xTa)=∂x∂(aTx)=a
其中, a ⃗ \vec{a} a 为常数向量,即 a ⃗ = ( a 1 , a 2 , ⋯ , a n ) T \vec{a}=(a_1,a_2,\cdots,a_n)^T a=(a1,a2,⋯,an)T。
证明:该式采用是是向量变元对标量函数的分布布局,结果如下: ∂ ( x ⃗ T a ⃗ ) ∂ x = ∂ ( a ⃗ T x ⃗ ) ∂ x ⃗ = ∂ ( a 1 x 1 + a 2 x 2 + ⋯ + a n x n ) ∂ x ⃗ = [ ∂ ( a 1 x 1 + a 2 x 2 + ⋯ + a n x n ) ∂ x 1 ∂ ( a 1 x 1 + a 2 x 2 + ⋯ + a n x n ) ∂ x 2 ⋮ ∂ ( a 1 x 1 + a 2 x 2 + ⋯ + a n x n ) ∂ x n ] = [ a 1 a 2 ⋮ a n ] = a ⃗ \begin{aligned} \frac{\partial(\vec{x}^{T}\vec{a})}{\partial x}& =\frac{\partial(\vec{a}^T\vec{x})}{\partial\vec{x}} \\ &=\frac{\partial(a_1x_1+a_2x_2+\cdots+a_nx_n)}{\partial\vec{x}} \\ &\left.=\left[\begin{array}{c}\frac{\partial(a_1x_1+a_2x_2+\cdots+a_nx_n)}{\partial x_1}\\\frac{\partial(a_1x_1+a_2x_2+\cdots+a_nx_n)}{\partial x_2}\\\vdots\\\frac{\partial(a_1x_1+a_2x_2+\cdots+a_nx_n)}{\partial x_n}\end{array}\right.\right] \\ &\left.=\left[\begin{array}{c}a_1\\a_2\\\vdots\\a_n\end{array}\right.\right] \\ &=\vec{a} \end{aligned} ∂x∂(xTa)=∂x∂(aTx)=∂x∂(a1x1+a2x2+⋯+anxn)= ∂x1∂(a1x1+a2x2+⋯+anxn)∂x2∂(a1x1+a2x2+⋯+anxn)⋮∂xn∂(a1x1+a2x2+⋯+anxn) = a1a2⋮an =a
(2): ∂ ( x ⃗ T x ⃗ ) ∂ x ⃗ = 2 x ⃗ \frac{\partial(\vec{x}^T\vec{x})}{\partial\vec{x}}=2\vec{x} ∂x∂(xTx)=2x证明:该式采用是是向量变元对标量函数的分布布局,结果如下: ∂ ( x ⃗ T x ⃗ ) ∂ x ⃗ = ∂ ( x 1 2 + x 2 2 + ⋯ + x n 2 ) ∂ x ⃗ = [ ∂ ( x 1 2 + x 2 2 + ⋯ + x n 2 ) ∂ x 1 ∂ ( x 1 2 + x 2 2 + ⋯ + x n 2 ) ∂ x 2 ⋮ ∂ ( x 1 2 + x 2 2 + ⋯ + x n 2 ) ∂ x n ] = [ 2 x 1 2 x 2 ⋮ 2 x n ] = 2 [ x 1 x 2 ⋮ x n ] = 2 x ⃗ \begin{aligned} \frac{\partial(\vec{x}^{T}\vec{x})}{\partial \vec{x}}& =\frac{\partial(x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2})}{\partial\vec{x}} \\ &\left.=\left[\begin{array}{c}\frac{\partial(x_1^2+x_2^2+\cdots+x_n^2)}{\partial x_1}\\\frac{\partial(x_1^2+x_2^2+\cdots+x_n^2)}{\partial x_2}\\\vdots\\\frac{\partial(x_1^2+x_2^2+\cdots+x_n^2)}{\partial x_n}\end{array}\right.\right] \\ &=\begin{bmatrix}2x_1\\2x_2\\\vdots\\2x_n\end{bmatrix} \\ &\left.=2\left[\begin{array}{c}x_1\\x_2\\\vdots\\x_n\end{array}\right.\right] \\ &=2\vec{x} \end{aligned} ∂x∂(xTx)=∂x∂(x12+x22+⋯+xn2)= ∂x1∂(x12+x22+⋯+xn2)∂x2∂(x12+x22+⋯+xn2)⋮∂xn∂(x12+x22+⋯+xn2) = 2x12x2⋮2xn =2 x1x2⋮xn =2x
(3):
∂
(
x
⃗
T
A
x
⃗
)
∂
x
⃗
=
A
x
⃗
+
A
T
x
⃗
\frac{\partial(\vec{x}^TA\vec{x})}{\partial\vec{x}}=A\vec{x}+{A}^T\vec{x}
∂x∂(xTAx)=Ax+ATx其中,
A
n
×
n
{A}_{n\times n}
An×n是常数矩阵,
A
n
×
n
=
(
a
i
j
)
i
=
1
,
j
=
1
n
,
n
{A}_{n\times n}=(a_{ij})_{i=1,j=1}^{n,n}
An×n=(aij)i=1,j=1n,n
证明: ∂ ( x ⃗ T A x ⃗ ) ∂ x ⃗ = ( x 1 , x 2 , … , x n ) ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ) ( x 1 x 2 ⋮ x n ) = ∂ ( a 11 x 1 x 1 + a 12 x 1 x 2 + ⋯ + a 1 n x 1 x n + a 21 x 2 x 1 + a 22 x 2 x 2 + ⋯ + a 2 n x 2 x n + ⋯ + a n 1 x n x 1 + a n 2 x n x 2 + ⋯ + a n n x n x n ) ∂ x ⃗ = [ ∂ ( a 11 x 1 x 1 + a 12 x 1 x 2 + ⋯ + a 1 n x 1 x n + a 21 x 2 x 1 + a 22 x 2 x 2 + ⋯ + a 2 n x 2 x n + ⋯ + a n 1 x n x 1 + a n 2 x n x 2 + ⋯ + a n n x n x n ) ∂ x 1 ∂ ( a 11 x 1 x 1 + a 12 x 1 x 2 + ⋯ + a 1 n x 1 x n + a 21 x 2 x 1 + a 22 x 2 x 2 + ⋯ + a 2 n x 2 x n + ⋯ + a n 1 x n x 1 + a n 2 x n x 2 + ⋯ + a n n x n x n ) ∂ x 2 ⋮ ∂ ( a 11 x 1 x 1 + a 12 x 1 x 2 + ⋯ + a 1 n x 1 x n + a 21 x 2 x 1 + a 22 x 2 x 2 + ⋯ + a 2 n x 2 x n + ⋯ + a n 1 x n x 1 + a n 2 x n x 2 + ⋯ + a n n x n x n ) ∂ x n ] = [ ( a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n ) + ( a 11 x 1 + a 21 x 2 + ⋯ + a n 1 x n ) ( a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n ) + ( a 12 x 1 + a 22 x 2 + ⋯ + a n 2 x n ) ⋮ ( a n 1 x 1 + a n 2 x 2 + ⋯ + a n n x n ) + ( a 1 n x 1 + a 2 n x 2 + ⋯ + a n n x n ) ] = [ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n ⋮ a n 1 x 1 + a n 2 x 2 + ⋯ + a n n x n ] + [ a 11 x 1 + a 21 x 2 + ⋯ + a n 1 x n a 12 x 1 + a 22 x 2 + ⋯ + a n 2 x n ⋮ a 1 n x 1 + a 2 n x 2 + ⋯ + a n n x n ] = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] [ x 1 x 2 ⋮ x n ] + [ a 11 a 21 ⋯ a n 1 a 12 a 22 ⋯ a n 2 ⋮ ⋮ ⋱ ⋮ a 1 n a 2 n ⋯ a n n ] [ x 1 x 2 ⋮ x n ] = A x ⃗ + A T x ⃗ (14) \begin{aligned} \frac{\partial( \vec{x}^T \pmb{A}\vec{x})}{\partial{\vec{x}}} &= (x_1,x_2,\dots,x_n)\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix}\begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} \\ &=\frac{\partial(a_{11}x_1x_1+a_{12}x_1x_2+\cdots+a_{1n}x_1x_n \\ +a_{21}x_2x_1+a_{22}x_2x_2+\cdots+a_{2n}x_2x_n \\ + \cdots \\ +a_{n1}x_nx_1+a_{n2}x_nx_2+\cdots+a_{nn}x_nx_n)}{\partial{\vec{x}}} \\\\ &= \begin{bmatrix} \frac{\partial(a_{11}x_1x_1+a_{12}x_1x_2+\cdots+a_{1n}x_1x_n \\ +a_{21}x_2x_1+a_{22}x_2x_2+\cdots+a_{2n}x_2x_n \\ + \cdots \\ +a_{n1}x_nx_1+a_{n2}x_nx_2+\cdots+a_{nn}x_nx_n)}{\partial{x_1}} \\ \frac{\partial(a_{11}x_1x_1+a_{12}x_1x_2+\cdots+a_{1n}x_1x_n \\ +a_{21}x_2x_1+a_{22}x_2x_2+\cdots+a_{2n}x_2x_n \\ + \cdots \\ +a_{n1}x_nx_1+a_{n2}x_nx_2+\cdots+a_{nn}x_nx_n)}{\partial{x_2}} \\ \vdots \\ \frac{\partial(a_{11}x_1x_1+a_{12}x_1x_2+\cdots+a_{1n}x_1x_n \\ +a_{21}x_2x_1+a_{22}x_2x_2+\cdots+a_{2n}x_2x_n \\ + \cdots \\ +a_{n1}x_nx_1+a_{n2}x_nx_2+\cdots+a_{nn}x_nx_n)}{\partial{x_n}} \end{bmatrix} \\\\ &= \begin{bmatrix} (a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n)+(a_{11}x_1+a_{21}x_2+\cdots+a_{n1}x_n) \\ (a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n)+(a_{12}x_1+a_{22}x_2+\cdots+a_{n2}x_n) \\ \vdots \\ (a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n)+(a_{1n}x_1+a_{2n}x_2+\cdots+a_{nn}x_n) \end{bmatrix} \\\\ &= \begin{bmatrix} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n \\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n \\ \vdots \\ a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n \end{bmatrix} +\begin{bmatrix} a_{11}x_1+a_{21}x_2+\cdots+a_{n1}x_n \\ a_{12}x_1+a_{22}x_2+\cdots+a_{n2}x_n \\ \vdots \\ a_{1n}x_1+a_{2n}x_2+\cdots+a_{nn}x_n \end{bmatrix} \\\\ &= \begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn} \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix} +\begin{bmatrix} a_{11}&a_{21}&\cdots&a_{n1}\\ a_{12}&a_{22}&\cdots&a_{n2}\\ \vdots&\vdots&\ddots&\vdots\\ a_{1n}&a_{2n}&\cdots&a_{nn} \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix} \\\\ &= \pmb{A}\vec{x}+\pmb{A}^T \vec{x} \end{aligned} \\\\ \tag{14} ∂x∂(xTAx)=(x1,x2,…,xn) a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann x1x2⋮xn =∂x∂(a11x1x1+a12x1x2+⋯+a1nx1xn+a21x2x1+a22x2x2+⋯+a2nx2xn+⋯+an1xnx1+an2xnx2+⋯+annxnxn)= ∂x1∂(a11x1x1+a12x1x2+⋯+a1nx1xn+a21x2x1+a22x2x2+⋯+a2nx2xn+⋯+an1xnx1+an2xnx2+⋯+annxnxn)∂x2∂(a11x1x1+a12x1x2+⋯+a1nx1xn+a21x2x1+a22x2x2+⋯+a2nx2xn+⋯+an1xnx1+an2xnx2+⋯+annxnxn)⋮∂xn∂(a11x1x1+a12x1x2+⋯+a1nx1xn+a21x2x1+a22x2x2+⋯+a2nx2xn+⋯+an1xnx1+an2xnx2+⋯+annxnxn) = (a11x1+a12x2+⋯+a1nxn)+(a11x1+a21x2+⋯+an1xn)(a21x1+a22x2+⋯+a2nxn)+(a12x1+a22x2+⋯+an2xn)⋮(an1x1+an2x2+⋯+annxn)+(a1nx1+a2nx2+⋯+annxn) = a11x1+a12x2+⋯+a1nxna21x1+a22x2+⋯+a2nxn⋮an1x1+an2x2+⋯+annxn + a11x1+a21x2+⋯+an1xna12x1+a22x2+⋯+an2xn⋮a1nx1+a2nx2+⋯+annxn = a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann x1x2⋮xn + a11a12⋮a1na21a22⋮a2n⋯⋯⋱⋯an1an2⋮ann x1x2⋮xn =Ax+ATx(14)上述的第一个等号是直接按照定义展开得到的,由于分子 x ⃗ T A x ⃗ \vec{x}^TA\vec{x} xTAx 实际上是一个标量,于是我们可以应用向量对标量函数的导数的求导法则来计算。通过观察我们可以发现结果布局是 n × 1 n \times 1 n×1 维的,且第一个分量的结果可以分成两项:是 A A A 的第一列的转置与 x ⃗ \vec{x} x 的内积以及 A A A 的第一行与 x ⃗ \vec{x} x 的内积,为此可以很自然地计算剩余的分量
(4): ∂ ( a ⃗ T x ⃗ x ⃗ T b ⃗ ) ∂ x ⃗ = a b T x ⃗ + b a T x ⃗ \frac{\partial(\vec{a}^T\vec{x}\vec{x}^T\vec{b})}{\partial\vec{x}}=ab^T\vec{x}+ba^T\vec{x} ∂x∂(aTxxTb)=abTx+baTx其中 a ⃗ , b ⃗ \vec{a},\vec{b} a,b 为常数向量, a ⃗ = ( a 1 , a 2 , ⋯ , a n ) T , b ⃗ = ( b 1 , b 2 , ⋯ , b n ) T \vec{a}=(a_1,a_2,\cdots,a_n)^T,\vec{b}=(b_1,b_2,\cdots,b_n)^T a=(a1,a2,⋯,an)T,b=(b1,b2,⋯,bn)T
证明:因为 a ⃗ T x ⃗ = x ⃗ T a ⃗ , x ⃗ T b ⃗ = b ⃗ T x ⃗ \vec{a}^T\vec{x}=\vec{x}^T\vec{a},\vec{x}^T\vec{b}=\vec{b}^T\vec{x} aTx=xTa,xTb=bTx ,所以有 ∂ ( a ⃗ T x ⃗ x ⃗ T b ⃗ ) ∂ x ⃗ = ∂ ( x ⃗ T a ⃗ b ⃗ T x ⃗ ) ∂ x ⃗ \frac{\partial(\vec{a}^T\vec{x}\vec{x}^T\vec{b})}{\partial\vec{x}}=\frac{\partial(\vec{x}^T\vec{a}\vec{b}^T\vec{x})}{\partial\vec{x}} ∂x∂(aTxxTb)=∂x∂(xTabTx)因为 a ⃗ b ⃗ T \vec{a}\vec{b}^T abT 是常数矩阵,于是可以利用公式 ∂ ( x ⃗ T A x ⃗ ) ∂ x ⃗ = A x ⃗ + A T x ⃗ \frac{\partial(\vec{x}^TA\vec{x})}{\partial\vec{x}}=A\vec{x}+{A}^T\vec{x} ∂x∂(xTAx)=Ax+ATx得到 ∂ ( a ⃗ T x ⃗ x ⃗ T b ⃗ ) ∂ x ⃗ = ∂ ( x ⃗ T a ⃗ b ⃗ T x ⃗ ) ∂ x ⃗ = a ⃗ b ⃗ T x ⃗ + b ⃗ a ⃗ T x ⃗ \frac{\partial(\vec{a}^T\vec{x}\vec{x}^T\vec{b})}{\partial\vec{x}}=\frac{\partial(\vec{x}^T\vec{a}\vec{b}^T\vec{x})}{\partial\vec{x}}=\vec{a}\vec{b}^T\vec{x}+\vec{b}\vec{a}^T\vec{x} ∂x∂(aTxxTb)=∂x∂(xTabTx)=abTx+baTx如上所述,证明完毕
2. 矩阵变元的实值标量函数
f ( X ) , X m × n = ( x i j ) i = 1 , j = 1 m , n f(\boldsymbol{X}),\boldsymbol{X}_{m\times n}=(x_{ij})_{i=1,j=1}^{m,n} f(X),Xm×n=(xij)i=1,j=1m,n利用梯度矩阵的形式,也就是矩阵变元的标量函数里的分母布局的形式,有: ∇ X f ( X ) = ∂ f ( X ) ∂ X m × n = [ ∂ f ∂ x 11 ∂ f ∂ x 12 ⋯ ∂ f ∂ x 1 n ∂ f ∂ x 21 ∂ f ∂ x 22 ⋯ ∂ f ∂ x 2 n ⋮ ⋮ ⋮ ⋮ ∂ f ∂ x m 1 ∂ f ∂ x m 2 ⋯ ∂ f ∂ x m n ] m × n \begin{aligned} \nabla_{X}f(\boldsymbol{X})& =\frac{\partial f(\boldsymbol{X})}{\partial\boldsymbol{X}_{m\times n}} \\ &=\begin{bmatrix}\frac{\partial f}{\partial x_{11}}&\frac{\partial f}{\partial x_{12}}&\cdots&\frac{\partial f}{\partial x_{1n}}\\\frac{\partial f}{\partial x_{21}}&\frac{\partial f}{\partial x_{22}}&\cdots&\frac{\partial f}{\partial x_{2n}}\\\vdots&\vdots&\vdots&\vdots\\\frac{\partial f}{\partial x_{m1}}&\frac{\partial f}{\partial x_{m2}}&\cdots&\frac{\partial f}{\partial x_{mn}}\end{bmatrix}_{m\times n} \end{aligned} ∇Xf(X)=∂Xm×n∂f(X)= ∂x11∂f∂x21∂f⋮∂xm1∂f∂x12∂f∂x22∂f⋮∂xm2∂f⋯⋯⋮⋯∂x1n∂f∂x2n∂f⋮∂xmn∂f m×n类似于向量变元的实值标量函数,给出下面给个4个原则,并选择性给出证明:
2.1 4个法则
我们设讨论的矩阵 X X X 是 m × n m \times n m×n 维的
(1):常数求导
与一元函数常数求导相同:结果为零矩阵,即
∂ c ∂ X = 0 m × n \frac{\partial c}{\partial X}=\mathbf{0}_{m\times n} ∂X∂c=0m×n其中, c c c 为常数
(2):线性法则
与一元函数求导线性法则相同:相加再求导等于求导再相加,常数提到外面,即: ∂ [ c 1 f ( X ) + c 2 g ( X ) ] ∂ X = c 1 ∂ f ( X ) ∂ X + c 2 ∂ g ( X ) ∂ X \frac{\partial[c_1f(X)+c_2g(X)]}{\partial X}=c_1\frac{\partial f(X)}{\partial X}+c_2\frac{\partial g(X)}{\partial X} ∂X∂[c1f(X)+c2g(X)]=c1∂X∂f(X)+c2∂X∂g(X)其中, c 1 , c 2 c_1,c_2 c1,c2 为常数。
(3):乘积法则
与一元函数求导乘积法则相同:前导后不导加前不导后导,即 ∂ [ f ( X ) g ( X ) ] ∂ X = ∂ f ( X ) ∂ X g ( X ) + f ( X ) ∂ g ( X ) ∂ X \frac{\partial[f(\boldsymbol{X})g(\boldsymbol{X})]}{\partial\boldsymbol{X}}=\frac{\partial f(\boldsymbol{X})}{\partial\boldsymbol{X}}g(\boldsymbol{X})+f(\boldsymbol{X})\frac{\partial g(\boldsymbol{X})}{\partial\boldsymbol{X}} ∂X∂[f(X)g(X)]=∂X∂f(X)g(X)+f(X)∂X∂g(X)
证明:由于矩阵变元的实值标量函数是对逐一每个元素 d x i j dx_{ij} dxij 的导数,为此利用向量变元的实值标量函数的乘积法则有: ∂ [ f ( X ) g ( X ) ] ∂ X = [ ∂ ( f g ) ∂ x 11 ∂ ( f g ) ∂ x 12 ⋯ ∂ ( f g ) ∂ x 1 n ∂ ( f g ) ∂ x 21 ∂ ( f g ) ∂ x 22 ⋯ ∂ ( f g ) ∂ x 2 n ⋮ ⋮ ⋮ ⋮ ∂ ( f g ) ∂ x m 1 ∂ ( f g ) ∂ x m 2 ⋯ ∂ ( f g ) ∂ x m n ] = [ ∂ f ∂ x 11 g + f ∂ g ∂ x 11 ∂ f ∂ x 12 g + f ∂ g ∂ x 12 ⋯ ∂ f ∂ x 1 n g + f ∂ g ∂ x 1 n ∂ f ∂ x 21 g + f ∂ g ∂ x 21 ∂ f ∂ x 22 g + f ∂ g ∂ x 22 ⋯ ∂ f ∂ x 2 n g + f ∂ g ∂ x 2 n ⋮ ⋮ ⋮ ⋮ ∂ f ∂ x m 1 g + f ∂ g ∂ x m 1 ∂ f ∂ x m 2 g + f ∂ g ∂ x m 2 ⋯ ∂ f ∂ x m n g + f ∂ g ∂ x m n ] = [ ∂ f ∂ x 11 ∂ f ∂ x 12 ⋯ ∂ f ∂ x 1 n ∂ f ∂ x 21 ∂ f ∂ x 22 ⋯ ∂ f ∂ x 2 n ⋮ ⋮ ⋮ ⋮ ∂ f ∂ x m 1 ∂ f ∂ x m 2 ⋯ ∂ f ∂ x m n ] g + f [ ∂ g ∂ x 11 ∂ g ∂ x 12 ⋯ ∂ g ∂ x 1 n ∂ g ∂ x 21 ∂ g ∂ x 22 ⋯ ∂ g ∂ x 2 n ⋮ ⋮ ⋮ ⋮ ∂ g ∂ x m 1 ∂ g ∂ x m 2 ⋯ ∂ g ∂ x m n ] = ∂ f ( X ) ∂ X g ( X ) + f ( X ) ∂ g ( X ) ∂ X (23) \begin{aligned} \frac{\partial{[f(\pmb{X})g(\pmb{X})]}}{\partial{\pmb{X}}} &= \begin{bmatrix} \frac{\partial{(fg)}}{\partial{x_{11}}} & \frac{\partial{(fg)}}{\partial{x_{12}}} & \cdots & \frac{\partial{(fg)}}{\partial{x_{1n}}} \\ \frac{\partial{(fg)}}{\partial{x_{21}}} & \frac{\partial{(fg)}}{\partial{x_{22}}} & \cdots & \frac{\partial{(fg)}}{\partial{x_{2n}}} \\ \vdots & \vdots & \vdots & \vdots \\ \frac{\partial{(fg)}}{\partial{x_{m1}}} & \frac{\partial{(fg)}}{\partial{x_{m2}}} & \cdots & \frac{\partial{(fg)}}{\partial{x_{mn}}} \end{bmatrix} \\\\ &= \begin{bmatrix} \frac{\partial{f}}{\partial{x_{11}}}g+f\frac{\partial{g}}{\partial{x_{11}}} & \frac{\partial{f}}{\partial{x_{12}}}g+f\frac{\partial{g}}{\partial{x_{12}}} & \cdots & \frac{\partial{f}}{\partial{x_{1n}}}g+f\frac{\partial{g}}{\partial{x_{1n}}} \\ \frac{\partial{f}}{\partial{x_{21}}}g+f\frac{\partial{g}}{\partial{x_{21}}} & \frac{\partial{f}}{\partial{x_{22}}}g+f\frac{\partial{g}}{\partial{x_{22}}} & \cdots & \frac{\partial{f}}{\partial{x_{2n}}}g+f\frac{\partial{g}}{\partial{x_{2n}}}\\ \vdots & \vdots & \vdots & \vdots \\ \frac{\partial{f}}{\partial{x_{m1}}}g+f\frac{\partial{g}}{\partial{x_{m1}}} & \frac{\partial{f}}{\partial{x_{m2}}}g+f\frac{\partial{g}}{\partial{x_{m2}}} & \cdots & \frac{\partial{f}}{\partial{x_{mn}}}g+f\frac{\partial{g}}{\partial{x_{mn}}} \end{bmatrix} \\\\ &=\begin{bmatrix} \frac{\partial{f}}{\partial{x_{11}}}&\frac{\partial{f}}{\partial{x_{12}}}&\cdots&\frac{\partial{f}}{\partial{x_{1n}}} \\ \frac{\partial{f}}{\partial{x_{21}}}&\frac{\partial{f}}{\partial{x_{22}}}&\cdots&\frac{\partial{f}}{\partial{x_{2n}}} \\ \vdots &\vdots & \vdots & \vdots\\ \frac{\partial{f}}{\partial{x_{m1}}}&\frac{\partial{f}}{\partial{x_{m2}}}&\cdots&\frac{\partial{f}}{\partial{x_{mn}}} \end{bmatrix}g + f\begin{bmatrix}\frac{\partial{g}}{\partial{x_{11}}}&\frac{\partial{g}}{\partial{x_{12}}}&\cdots&\frac{\partial{g}}{\partial{x_{1n}}} \\ \frac{\partial{g}}{\partial{x_{21}}}&\frac{\partial{g}}{\partial{x_{22}}}&\cdots&\frac{\partial{g}}{\partial{x_{2n}}} \\ \vdots &\vdots & \vdots & \vdots\\ \frac{\partial{g}}{\partial{x_{m1}}}&\frac{\partial{g}}{\partial{x_{m2}}}&\cdots&\frac{\partial{g}}{\partial{x_{mn}}} \end{bmatrix} \\\\ &=\frac{\partial f(\pmb{X})}{\partial{\pmb{X}}}g(\pmb{X}) +f(\pmb{X})\frac{\partial g(\pmb{X})}{\partial{\pmb{X}}} \end{aligned} \\\\ \tag{23} ∂X∂[f(X)g(X)]= ∂x11∂(fg)∂x21∂(fg)⋮∂xm1∂(fg)∂x12∂(fg)∂x22∂(fg)⋮∂xm2∂(fg)⋯⋯⋮⋯∂x1n∂(fg)∂x2n∂(fg)⋮∂xmn∂(fg) = ∂x11∂fg+f∂x11∂g∂x21∂fg+f∂x21∂g⋮∂xm1∂fg+f∂xm1∂g∂x12∂fg+f∂x12∂g∂x22∂fg+f∂x22∂g⋮∂xm2∂fg+f∂xm2∂g⋯⋯⋮⋯∂x1n∂fg+f∂x1n∂g∂x2n∂fg+f∂x2n∂g⋮∂xmn∂fg+f∂xmn∂g = ∂x11∂f∂x21∂f⋮∂xm1∂f∂x12∂f∂x22∂f⋮∂xm2∂f⋯⋯⋮⋯∂x1n∂f∂x2n∂f⋮∂xmn∂f g+f ∂x11∂g∂x21∂g⋮∂xm1∂g∂x12∂g∂x22∂g⋮∂xm2∂g⋯⋯⋮⋯∂x1n∂g∂x2n∂g⋮∂xmn∂g =∂X∂f(X)g(X)+f(X)∂X∂g(X)(23)即证
(4):商法则
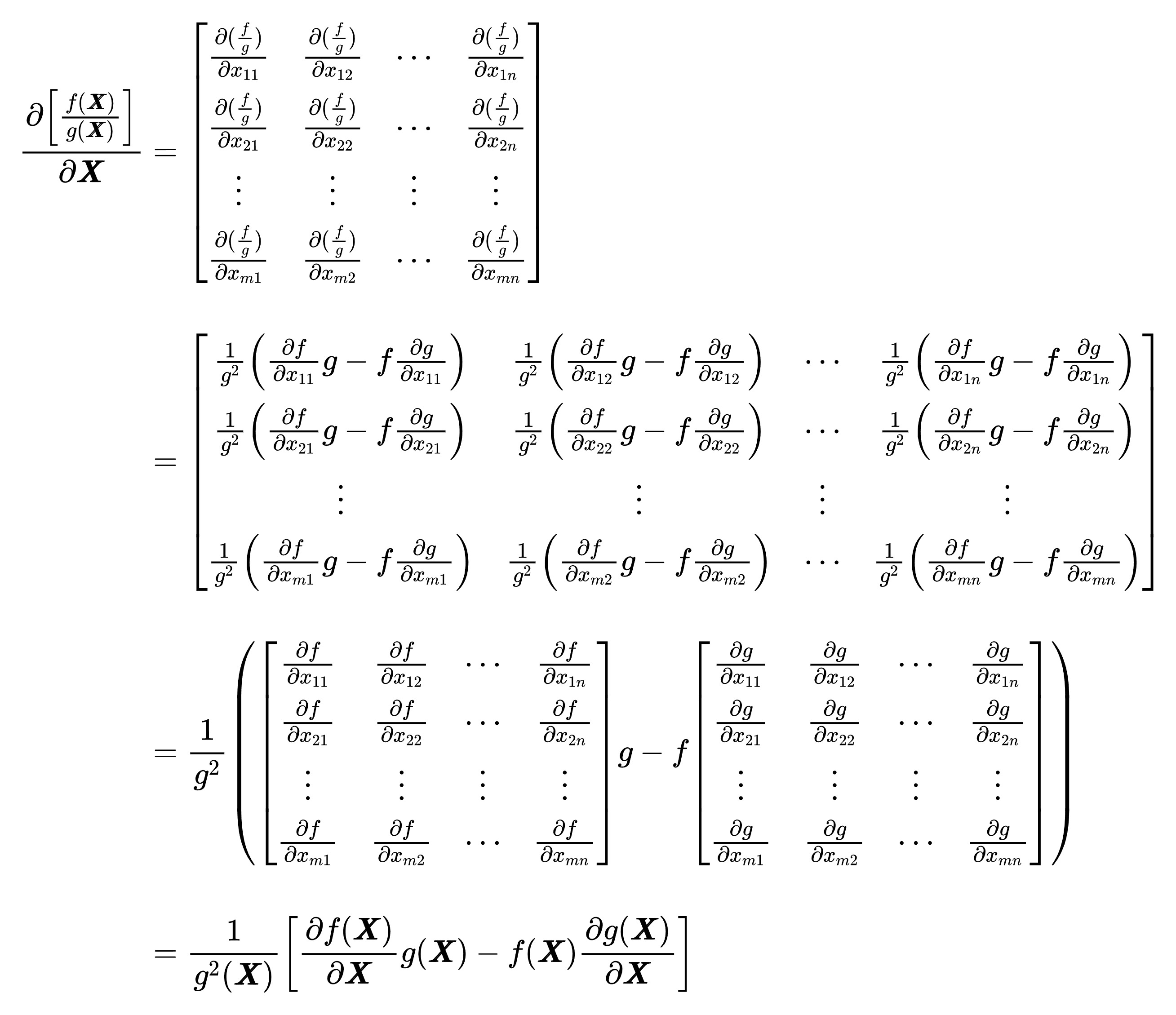
与一元函数求导商法则相同:(上导下不导 减 上不导下导)除以(下的平方): ∂ [ f ( X ) g ( X ) ] ∂ X = 1 g 2 ( X ) [ ∂ f ( X ) ∂ X g ( X ) − f ( X ) ∂ g ( X ) ∂ X ] \begin{aligned}&\frac{\partial\left[\frac{f(\boldsymbol{X})}{g(\boldsymbol{X})}\right]}{\partial\boldsymbol{X}}=\frac1{g^2(\boldsymbol{X})}\Big[\frac{\partial f(\boldsymbol{X})}{\partial\boldsymbol{X}}g(\boldsymbol{X})-f(\boldsymbol{X})\frac{\partial g(\boldsymbol{X})}{\partial\boldsymbol{X}}\Big]\\\end{aligned} ∂X∂[g(X)f(X)]=g2(X)1[∂X∂f(X)g(X)−f(X)∂X∂g(X)]其中, g ( X ) ≠ 0 g(\boldsymbol{X})\neq0 g(X)=0.
证明(由于Latex太长了放不下,就用图片吧):
2.2 常用公式
(1):
∂ ( a ⃗ T X b ⃗ ) ∂ X = a ⃗ b ⃗ T \frac{\partial(\vec{a}^T\boldsymbol{X}\vec{b})}{\partial\boldsymbol{X}}=\vec{a}\vec{b}^T ∂X∂(aTXb)=abT
其中, a ⃗ m × 1 , b ⃗ n × 1 \vec{a}_{m\times1},\vec{b}_{n\times1} am×1,bn×1 为常数向量, a ⃗ = ( a 1 , a 2 , ⋯ , a m ) T , b ⃗ = ( b 1 , b 2 , ⋯ , b n ) T \vec{a}_{=}(a_1,a_2,\cdots,a_m)^T,\vec{b}=(b_1,b_2,\cdots,b_n)^T a=(a1,a2,⋯,am)T,b=(b1,b2,⋯,bn)T
证明(同样因为Latex公式太长了,就不放了)

(2):
∂ ( a ⃗ T X T b ⃗ ) ∂ X = b ⃗ a ⃗ T \frac{\partial(\vec{a}^T\boldsymbol{X}^T\vec{b})}{\partial\boldsymbol{X}}=\vec{b}\vec{a}^T ∂X∂(aTXTb)=baT其中 a ⃗ = ( a 1 , a 2 , ⋯ , a n ) T , b ⃗ = ( b 1 , b 2 , ⋯ , b m ) T \vec{a}_=(a_1,a_2,\cdots,a_n)^T,\vec{b}=(b_1,b_2,\cdots,b_m)^T a=(a1,a2,⋯,an)T,b=(b1,b2,⋯,bm)T
证明:我们发现分子实际上是一个标量,因为标量的转置等于标量自己,所以有
∂
(
a
⃗
T
X
T
b
⃗
)
∂
X
=
∂
(
a
⃗
T
X
T
b
⃗
)
T
∂
X
=
∂
(
b
⃗
T
X
a
⃗
)
∂
X
\frac{\partial(\vec{a}^T\boldsymbol{X}^T\vec{b})}{\partial\boldsymbol{X}}=\frac{\partial(\vec{a}^T\boldsymbol{X}^T\vec{b})^T}{\partial\boldsymbol{X}}=\frac{\partial(\vec{b}^T\boldsymbol{X}\vec{a})}{\partial\boldsymbol{X}}
∂X∂(aTXTb)=∂X∂(aTXTb)T=∂X∂(bTXa)由上述已经证明的公式
∂
(
a
⃗
T
X
b
⃗
)
∂
X
=
a
⃗
b
⃗
T
\frac{\partial(\vec{a}^T\boldsymbol{X}\vec{b})}{\partial\boldsymbol{X}}=\vec{a}\vec{b}^T
∂X∂(aTXb)=abT可以得到
∂
(
a
⃗
T
X
T
b
⃗
)
∂
X
=
∂
(
a
⃗
T
X
T
b
⃗
)
T
∂
X
=
∂
(
b
⃗
T
X
a
⃗
)
∂
X
=
b
⃗
a
⃗
T
\frac{\partial(\vec{a}^T\boldsymbol{X}^T\vec{b})}{\partial\boldsymbol{X}}=\frac{\partial(\vec{a}^T\boldsymbol{X}^T\vec{b})^T}{\partial\boldsymbol{X}}=\frac{\partial(\vec{b}^T\boldsymbol{X}\vec{a})}{\partial\boldsymbol{X}}=\vec{b}\vec{a}^T
∂X∂(aTXTb)=∂X∂(aTXTb)T=∂X∂(bTXa)=baT
(3):
∂ ( a ⃗ T X X T b ⃗ ) ∂ X = a ⃗ b ⃗ T X + b ⃗ a ⃗ T X \frac{\partial(\vec{a}^T\boldsymbol{X}\boldsymbol{X}^T\vec{b})}{\partial\boldsymbol{X}}=\vec{a}\vec{b}^T\boldsymbol{X}+\vec{b}\vec{a}^T\boldsymbol{X} ∂X∂(aTXXTb)=abTX+baTX
其中, a ⃗ m × 1 , b ⃗ m × 1 \vec{a}_{m\times1},\vec{b}_{m\times1} am×1,bm×1 为常数向量, a ⃗ = ( a 1 , a 2 , ⋯ , a m ) T , b ⃗ = ( b 1 , b 2 , ⋯ , b m ) T \vec{a}_{=}(a_1,a_2,\cdots,a_m)^T,\vec{b}=(b_1,b_2,\cdots,b_m)^T a=(a1,a2,⋯,am)T,b=(b1,b2,⋯,bm)T
由于证明比较长,就不给出了,感兴趣的读者可以去参考中参考原作者的证明。证明过程实际是按照矩阵变元对实值标量函数的求定义,对每一个元素求导后证明的,过程比较复杂,当然了后面会有更为简洁的办法。
(4):
∂ ( a ⃗ T X T X b ⃗ ) ∂ X = X a ⃗ b ⃗ T + X b ⃗ a ⃗ T \frac{\partial(\vec{a}^T\boldsymbol{X}^T\boldsymbol{X}\vec{b})}{\partial\boldsymbol{X}}=\boldsymbol{X}\vec{a}\vec{b}^T+\boldsymbol{X}\vec{b}\vec{a}^T ∂X∂(aTXTXb)=XabT+XbaT
本次笔记到这里就结束了,由于我只是对原内容的学习,当然不会写的太过详细,因此感兴趣的读者可以去读原文哦(再三强调~)
写到这不免会觉得后面那几个求导公式按照定义推导非常麻烦,而且过程也不易懂,好在如果利用矩阵的迹与一阶实矩阵微分 d X d X dX 就可以简洁地证明上述的公式,为此让我们在下一篇博文中看看是如何做的吧(特别安利~)
参考
矩阵求导公式的数学推导(矩阵求导——基础篇)
张贤达《矩阵分析与应用(第二版)》