显式利用用户画像的多兴趣建模

目前在多兴趣建模中，用户侧的特征包括用户基础画像特征（年龄、性别、地域等）、用户在当前场景的静态兴趣画像特征（短期兴趣画像、长期兴趣画像）、交互的历史正向行为序列特征（正向物料id序列、正向物料类目序列、正向行为间隔序列等）。不论是基础画像、静态兴趣画像，都称为用户画像，经过Embedding层之后，与用户序列特征经过兴趣编码层提取后的兴趣Embedding拼接后进入最后的MLP。这里直接简单的拼接应该有更有效的方式来处理，有一篇paper使用attention的方式较好的结合了兴趣Embedding和用户画像Embedding。

论文地址：https://dl.acm.org/doi/pdf/10.1145/3477495.3532073

整体结构

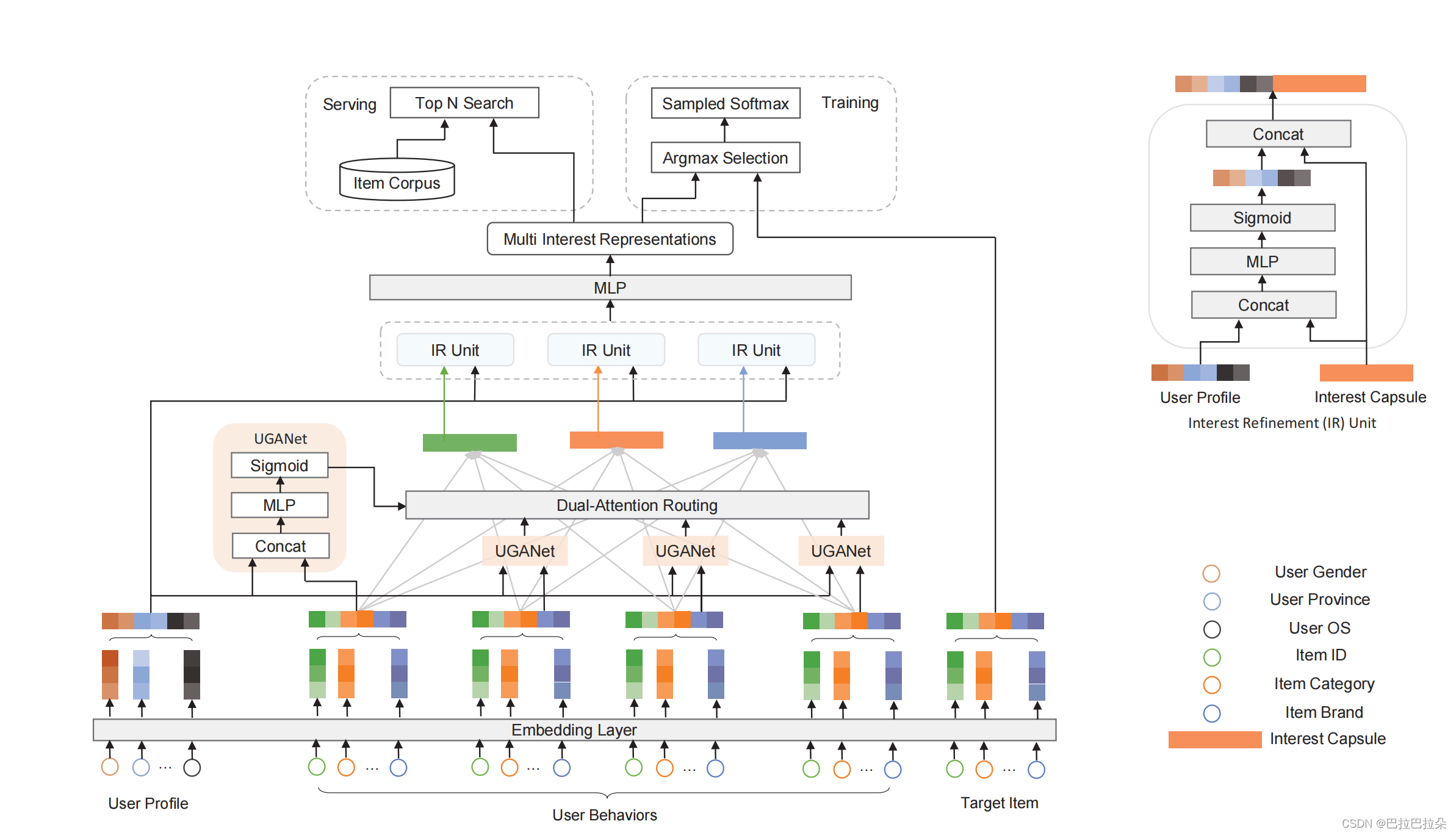
多兴趣编码前

用户序列在输出多兴趣编码层之前，对序列每个正向行为的Embedding和用户画像计算attention分数，即计算每个正向行为和用户画像的相关性。然后attention分数乘到行为的Embedding上面，即对用户画像相关程度高的行为进行强化，对用户还行相关程度低的行为降权弱化，这个操作类似于对用户序列进行去噪。

其中计算attention分数的方式如下，这里也是用到了一个网络，论文中称为user-guided attention Network，${\mathbf{e}}_i$是用户序列Embedding,${\mathbf{e}}_u$是用户画像Embedding，$[{\mathbf{e}}_i,{\mathbf{e}}_u]$表示用户画像Embedding和行为Embedding拼接成一个Embedding，${\mathbf{W}}_i^T$是学习的参数，$a_i$是attention分数。

$$a_i=sigmoid({\mathbf{W}}_2^{T}ReLU({\mathbf{W}}_1^T[{\mathbf{e}}_i,{\mathbf{e}}_u]+{\mathbf{b}}_1)+b_2)$$

计算出的attention分数再乘回到序列Embedding上面，作为兴趣编码层的输入（如果是capsule编码，则计算方式如下）
$$z_j=\sum _{i=1}^T{a}_i{c}_{ij}{\mathbf{W}}_j{\mathbf{e}}_j$$

多兴趣编码后

经过多兴趣编码之后，产生的多个兴趣向量，需要再度与用户画像进行兴趣精调，即用产生的兴趣向量和用户画像向量再次计算相关性，对相关性高的兴趣进行强化。论文中称这部分为IR Unit。

假设编码出了$K$个兴趣向量，${\mathbf{v}}_k$表示一个兴趣向量，${\mathbf{e}}_u$表示用户画像Embedding，${\mathbf{o}}_k$表示最终的兴趣向量。精调过程如下

$${\mathbf{o}}_k=MLP([{\mathbf{o}}_k,{\mathbf{e}}_u])k=1,2,...,K$$

不得不说，利用用户画像的这个方式挺有效的。兴趣编码之前，对每个行为序列根据用户画像进行去噪提纯；兴趣编码之后，对每个兴趣向量根据用户画像进行精调。

其他策略

这个paper还提出了一个hard negetive策略
使用argmax从用户兴趣向量池${\mathbf{O}}_u$中选择出和目标物料${\mathbf{e}}_t$最匹配的兴趣向量${\mathbf{o}}_k$

$${\mathbf{o}}_k={\mathbf{O}}_u[argmax({\mathbf{O}}_u^T{\mathbf{e}}_t)]$$
那么基于这个用户兴趣${\mathbf{o}}_k$，最可能的交互物料$x_t$可以由最大化$p(x_t|u)$得到

$$p(x_t|u)=\frac{exp({\mathbf{o}}_k^T{\mathbf{e}}_t)}{{\sum }_{j\in I}exp({\mathbf{o}}_k^T{\mathbf{e}}_j)}$$
这里面兴趣向量${\mathbf{o}}_k$是和正向物料$x_t$最相关的，计算负样本中的$x_j$的相关性也是用这个兴趣向量来计算的，训练和推断时有个较大的gap，因为$o_k$和目标物料$x_t$明显相关，但是和其他物料$x_t$明显无关。因此可以构造hard negetive，argmax操作不仅仅包括正向物料，也报告负向物料，即选出每个物料最相关的兴趣向量，不论这个物料是正向的还是负向的。

$${\mathbf{o}}_k^{(q)}={\mathbf{O}}_u[argmax({\mathbf{O}}_u^T{\mathbf{e}}_q)]$$

$$p(x_t|u)=\frac{exp((o_k^{(t)}{)}^T{\mathbf{e}}_t)}{{\sum }_{j\in I}exp((o_k^{(j)}{)}^T{\mathbf{e}}_j)}$$

损失函数如下：
$$L=\sum _{u\in U}\sum _{x_t\in I_u}-\log (p(x_t|u))$$