优先队列+模拟
根据题目描述模拟。
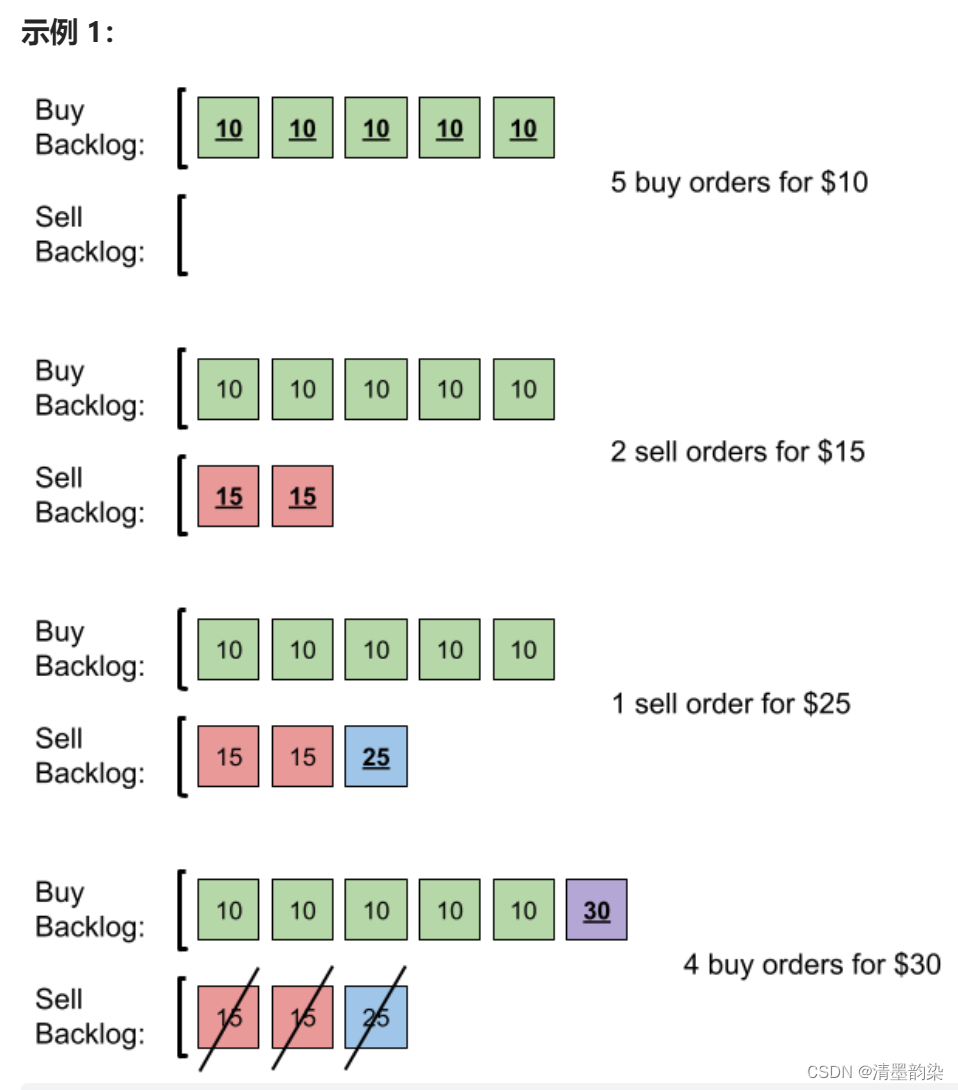
如果该订单是一笔采购订单 buy ,则可以查看积压订单中价格 最低 的销售订单 sell 。提示我们,建立小根堆,维护价格最低的销售订单sell 。
反之亦然,如果该订单是一笔销售订单 sell ,则可以查看积压订单中价格 最高 的采购订单 buy 。提示我们,建立大根堆,维护价格最高的采购订单 buy 。
为了使答案返回积压订单数量,我们让优先队列保存元素类型pair<int,int>,同时记录{价格,数量}。
遍历 order ,记录类型、价格、数量。根据类型操作即可。操作流程请看题目描述。
提示
buy和sell操作具有对称性,写好一个操作,另一个操作就好写了,照着逻辑改改。- 本题重在模拟和容器使用,模拟是思路,容器使用是代码模板。
题目描述


核心代码
class Solution {
public:
int getNumberOfBacklogOrders(vector<vector<int>>& orders) {
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> qsell;
priority_queue<pair<int,int>> qbuy;
for(auto &x:orders){
int type = x[2],amount = x[1], price = x[0];
if(0==type){
while(qsell.size()&&price>=qsell.top().first&&amount) {
if(amount>=qsell.top().second) {
amount -= qsell.top().second;
qsell.pop();
}else {
auto t = qsell.top();
t.second -= amount;
amount = 0;
qsell.pop();
qsell.push(t);
}
}
if(amount) qbuy.push({price,amount});
}else{
while(qbuy.size()&&price<=qbuy.top().first&&amount) {
if(amount>=qbuy.top().second) {
amount -= qbuy.top().second;
qbuy.pop();
}else {
auto t = qbuy.top();
t.second -= amount;
amount = 0;
qbuy.pop();
qbuy.push(t);
}
}
if(amount) qsell.push({price,amount});
}
}
int ans = 0 ;
const int mod = 1e9 + 7;
while(qsell.size()) ans = (ans + qsell.top().second)%mod , qsell.pop();
while(qbuy.size()) ans = (ans + qbuy.top().second)%mod , qbuy.pop();
return ans;
}
};
- 时间复杂度 : O ( n l o g n ) O(nlogn) O(nlogn) , n n n 是订单总数,遍历订单,将订单加入优先队列的时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn) 。
- 空间复杂度 : O ( n ) O(n) O(n) , 优先队列的空间复杂度 O ( n ) O(n) O(n) 。
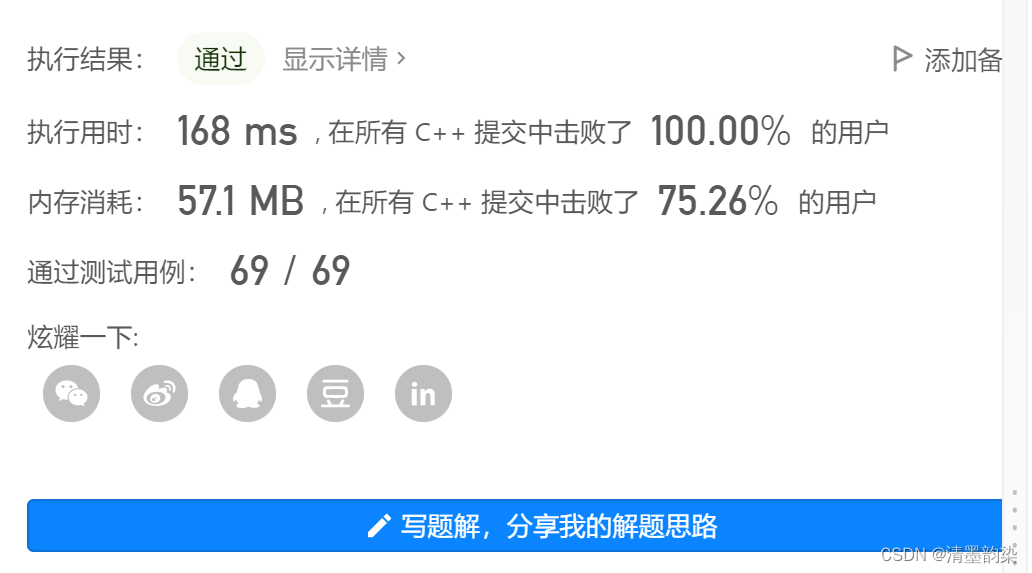
AC
致语
- 理解思路很重要!
- 欢迎读者在评论区留言,墨染看到就会回复的。